Алгоритм Дейкстры-Прима

Дейкстра и Прим предложили так называемый «жадный» алгоритм построения МОД. «Жадные» алгоритмы действуют, используя в каждый момент часть исходных данных и принимая лучшее решение на основе этой части. В рассматриваемом случае на каждом шаге имеется множество ребер, которые могут быть присоединены к уже построенной части остовного дерева, из них выбирается ребро с наименьшим весом. Вершины графа разбиваются на три класса: вершины, вошедшие в уже построенную часть дерева, вершины, окаймляющие построенную часть, и еще не рассмотренные вершины. Алгоритм начинает работу с произвольной вершины графа, которая включается в остовное дерево. Все вершины, соединенные (соседние) с данной, заносятся в кайму. Затем выполняется цикл поиска ребра с наименьшим весом, соединяющего уже построенную часть остовного дерева с каймой; это ребро вместе с новой вершиной добавляется в дерево и происходит обновление каймы таким образом, чтобы список ребер из дерева в кайму включал ребра с наименьшими весами. После того, как в дерево попадут все вершины, работа будет закончена. Словесный алгоритм приведен ниже:

Шаг 1. Выбрать начальный узел

Шаг 2. Сформировать начальную кайму, состоящую из вершин, соседних с начальным узлом

Шаг 3. В графе есть вершины, не попавшие в дерево?

Если да, то переход на Шаг 4.

Иначе – переход на Шаг 9.

Шаг 4. Выбрать ребро из дерева в кайму с наименьшим весом

Шаг 5. Добавить конец ребра к дереву

Шаг 6. Изменить кайму, для чего добавить в кайму вершины, соседние с новой

Шаг 7. Обновить список ребер из дерева в кайму так, чтобы он состоял из ребер наименьшего веса

Шаг 8. Переход на Шаг 3

Шаг 9. Конец

На Рис. 3.6 изображен исходный граф:

Рис. 3.6. Исходный граф

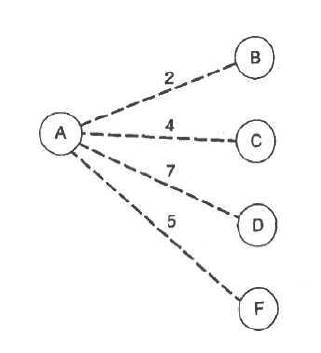
Рис. 3.7. Добавление первой вершины. Пунктиры ведут к вершинам каймы

Рис. 3.8. Добавление второй и третьей вершин

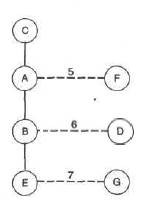
Рис. 3.9. Добавление четвертой и пятой вершин

Рис. 3.10. Заключительные шаги алгоритма Дейкстры-Прима

Дата добавления: 2015-10-13