Алгоритм Крускала

Другой алгоритм построения МОД предложил Крускал. Алгоритм начинает работу с пустого дерева. К нему добавляются ребра в порядке возрастания их весов до тех пор, пока не будет получен набор ребер, объединяющий все вершины графа. В процессе выполнения необходимо не допускать добавление ребер, приводящих к появлению цикла в создаваемом дереве. Если ребра закончатся до того, как все вершины будут соединены между собой, это означает, что граф был несвязным, и полученный результат представляет собой объединение МОД всех его компонент связности. Пример алгоритма приведен ниже:

1. Отсортировать ребра в порядке возрастания весов

2. Инициализировать структуру разбиений

edgeCount=l

while edgeCount<=E and includedCount<=N-l do

parentl=FindRoot(edge[edgeCount].start)

parent2=FindRoot(edge[edgeCount].end)

if parentl/=parent2 then

добавить edge[edgeCount] в остовное дерево

includedCount=includedCount+l

Union(parent1,parent2)

end if

edgeCount=edgeCount+l

end while

Для иллюстрации действия алгоритма будем использовать граф, приведенный на Рис. 3.6.

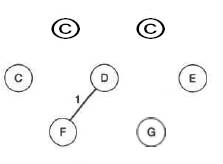
Рис. 3.11. Добавление первого ребра

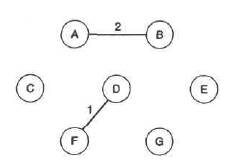
Рис. 3.12. Добавление второго и третьего ребра

Рис. 3.13. Добавление четвертого и пятого ребер

Рис. 3.14. Заключительные шаги алгоритма Крускала

Дата добавления: 2015-10-13