Случай разных совокупностей параметров g при разных значениях l

Некоторые различия между рассматриваемыми правилами реше­ния могут возникнуть, если разным значениям соответствуют различ­ные совокупности параметров 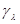. Практически такая ситуация может возникнуть только в том случае, когда множество значений дискрет­но, то есть состоит из изолированных точек (). При этом апостериорный риск (6.5.8) может быть записан в виде

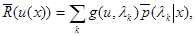(6.5.18)

где - оценочное значение апостериорной вероятности k -ro ди­скретного значения , которое определяется следующим выражением

(6.5.19)

- оценка максимального правдоподобия параметров 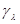; m _k - число неизвестных параметров плотности вероятности 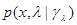; - значе­ние матрицы (6.5.6); - значение функции при .

Для того чтобы правило решения, получающееся минимизацией (6.5.18), было вполне определенным, необходимо как-то задать величи­ны (). Если функция не задана, то, используя предполагав­шееся ранее медленное изменение этой функции, можно оценить эти величины следующим образом:

(6.5.20)

где - эффективный объем области сосредоточения параметров 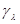для . В частности, если область значений параметров 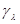ограни­чена, то по порядку величины совпадает с объемом этой области для .

ВЫВОДЫ

В следующих двух главах рассмотрим ряд важных деталей, свя­занных с применением адаптивного байесова подхода при параметри­ческой и непараметрической априорной неопределенности, а сейчас, допуская некоторые повторения, кратко обсудим основные результаты этой главы.

1. Как и обычный байесов, адаптивный байесов подход основан на выборе правила решения u = u(x), минимизирующего ожидаемые при данном состоянии имеющихся знаний потери. Отличие заключается в том, что из-за недостатка априорных сведений вместо точной коли­чественной меры ожидаемых потерь - апостериорного риска - вводит­ся его оценка, максимально использующая имеющиеся данные наблю­дения и ограниченные априорные сведения. Этот принцип применяется как при параметрической, так и при непараметрической априорной не­определенности.

2. Если использованная при нахождении адаптивного байесова правила решения оценка апостериорного риска состоятельна, то это правило удовлетворяет большинству из принципов предпочтения (прин­ципов оптимальности), возможных в условиях априорной неопределен­ности и рассмотренных в § 4.3, то есть действительно этот подход дает наилучшие в условиях априорной неопределенности правила решения. Состоятельность оценки апостериорного риска обеспечивается, если в условиях параметрической априорной неопределенности заменить неизвестные значения параметров , входящих в распределение вероят­ности для х и , состоятельными оценками этих параметров, а в усло­виях непараметрической априорной неопределенности подобно тому, как это сделано в примере 2 § 6.1, заменить при вычислении апостери­орного риска (или только его минимума) операцию математического ожидания эмпирическим осреднением по совокупности имеющихся дан­ных наблюдения.

3. При параметрической априорной неопределенности процедура нахождения адаптивного байесова правила решения принципиально весьма проста: она сводится к замене в обычном байесовом правиле решения u = uo(x, ), полученном для известного значения , этого зна­чения его состоятельной оценкой (х), найденной с использованием имеющихся данных наблюдения.

Если при этом оценка (х) удовлетворяет дополнительному требо­ванию (6.2.12), которое при оговоренных выше условиях приводит к необходимости выбора в качестве (x) оценки максимального прав­доподобия *(x) (см. уравнения (6.2.15), (6.3.3)), то адаптивное байесово правило решения удовлетворяет еще одному важному принципу оптимальности: оно является равномерно наилучшим приближением к обычному (абсолютно оптимальному) байесову правилу решения и обеспечивает минимум максимального отклонения среднего риска от минимального байесова риска.

4. Если вместо требования равномерно наилучшего приближения принять требование наилучшего приближения в среднем с весом () к обычному байесову правилу решения, то соответствующее приближенно оптимальное правило решения u = u*(x) находится мини­мизацией усредненного по среднего риска R(u(x), ), а сама функция может быть формально интерпретирована как плотность вероятности для неизвестных параметров . При этом правило решения u*(х) является обычным байесовым правилом для совместного распре­деления вероятности х и с плотностью (6.5.2), получающейся усред­нением по неизвестным параметрам с плотностью вероятности .

Естественно, что это правило решения может быть найдено совер­шенно точно с помощью обычной байесовой процедуры при любой . Однако если функция является относительно плавной - мало изменяется в пределах разброса оценки максимального правдо­подобия для относительно истинного значения (количественные требования определяются неравенствами (6.5.7)), то правило решения u*(х) совершенно аналогично адаптивному байесову правилу u₀(х, ) может быть найдено минимизацией состоятельных оценок апо­стериорного риска (6.5.8), (6.5.17), (6.5.18), для нахождения которых не требуется детального задания или вообще знания функции .

5. Во многих случаях оба правила решения (u₀(x, ) и u*(х)) просто совпадают. Это, конечно, свидетельствует о том, что средний риск любого из них отличается от минимального байесова риска на по­стоянную при всех значениях величину, которая по определению этих правил решения минимальна и в силу их асимптотической оптималь­ности стремится к нулю с ростом качества и объема данных наблюдения. Выбор между этими правилами в случае их несовпадения зависит от того, что более важно в данной конкретной задаче: наилучшее в среднем приближение к абсолютно оптимальному правилу решения или приближение, обеспечивающее минимум максимального откло­нения.

Дата добавления: 2015-09-03