
Читайте также:
|
Кафедра энергофизики
Лабораторная работа
Определение коэффициента диффузии жидкостей теневым методом
Минск 2009
Изучение явления диффузии имеет существенное значение для исследования разнообразных физико-технических процессов в технологии, физической химии и биологии, а также представляет практический интерес в области аэродинамики, пищевой и технологической промышленности. Изучение диффузии жидких сред является одним из основных методов исследования их структуры. Измерение коэффициентов диффузии различных членов гомологического ряда (например, предельных углеводородов в воде) и сравнение их с молекулярными весами дает информацию о подвижности растворенных макромолекул и служит источником сведений об их геометрических и гидродинамических характеристиках.
При изучении нестационарных процессов тепло- и массопереноса предпочтение отдается оптическим методам: теневому, интерференционному и голографическому. Их преимуществами является бесконтактность (что не вносит искажений в протекающий процесс) и практическое отсутствие инерционных погрешностей (что позволяет исследовать быстро протекающие процессы). К недостаткам этих методов можно отнести необходимость оптической прозрачности исследуемой среды и наличие высококачественных фотоматериалов для получения интерферограмм.
Макроскопическая направленная диффузия в растворе возникает при ненулевой величине пространственного градиента концентрации растворенного вещества. Процесс описывается двумя уравнениями переноса. Первое из них:
 ,
,
где j – поток вещества, диффундирующего в направлении умеьшения концентрации, D – коэффициент диффузии, с – концентрация компонента смеси. Это уравнение называется первым законом Фика и описывает стационарный процесс диффузии.
Второе уравнение (второй закон Фика) описывает нестационарную диффузию. В отсутствии конвекции оно запысывается в виде:
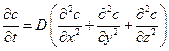
Явления переноса описываются параболическим уравнением в частных производных, которое имеет вид
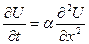 , (1)
, (1)
где α - коэффициент диффизии тепла или массы.
При изучении явления переноса тепла 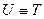 (температура),
(температура), 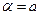 [м2 /с] – коэффициент температуропроводности; при переносе массы
[м2 /с] – коэффициент температуропроводности; при переносе массы 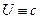 (концентрация),
(концентрация), 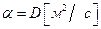 - коэффициент диффузии.
- коэффициент диффузии.
Рассматривая в дальнейшем процессы одномерной диффузии, запишем (1) в виде:
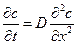 (2)
(2)
Методы, определяющие коэффициент диффузии, основаны на решении (2) при определенных краевых условиях, под которыми понимается совокупность начальных и граничных условий.
В физико-химических исследованиях широко используется модель полупространства, т.е. бесконечной области, имеющей только одну ограничительную плоскость, являющуюся началом отсчета. Математически условия задачи для полупространства формулируются следующим образом: требуется решить (2) при следующих начальных и граничных условиях:
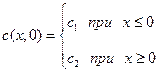 (3)
(3)
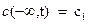 (4)
(4)
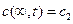 (5)
(5)
Решение уравнения (2) ищем в виде:
с(x,t) = T(t)X(x)
X(x) 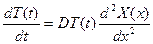
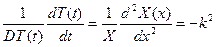
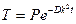
X =A’ cos kx + B’ sin kx
Частное решение уравнения (2):
с(x, t) = (A cos kx + B sin kx) exp(-k2Dt) (A=PA’, B=PB’)
Общее решение представляется в виде суммы частных решений
c(x,t) = 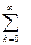 (Аk cos kx + Bk sin kx) exp(-k2Dt) (6)
(Аk cos kx + Bk sin kx) exp(-k2Dt) (6)
Так как объем диффундирующего вещества неограничен и параметр k является произвольным, то можно перейти от суммирования к интегра-лу по параметру k от -∞ до +∞:
с(x,t) = 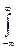 (Akcos kx + Bksin kx) exp(-k2Dt)dk (7)
(Akcos kx + Bksin kx) exp(-k2Dt)dk (7)
При t=0 имеем:
с(х,0) = 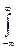 (Akcos kx + Bksin kx)dk
(Akcos kx + Bksin kx)dk
Коэффициенты Аk и Bk выражаются формулами:
Аk = 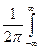 с(z,0) cos kz dz
с(z,0) cos kz dz
(8)
Bk = 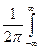 с(z,0) sin kz dz
с(z,0) sin kz dz
Подставив эти выражения в уравнение (7), получим
C(x,t)= 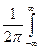 с(z,0) dz
с(z,0) dz 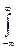 exp (-k2Dt) [cos(kz)×cos(kx)+sin(kz)×sin(kx)]dk
exp (-k2Dt) [cos(kz)×cos(kx)+sin(kz)×sin(kx)]dk
= 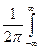 c(z,0) dz
c(z,0) dz 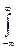 exp(-k2Dt)×cosk(z-x)dk
exp(-k2Dt)×cosk(z-x)dk
Так как функция cos чётная, имеем
c(x,t) = 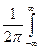 c(z,0) dz
c(z,0) dz 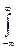 exp(-k2Dt)×cosk(z-x)dk
exp(-k2Dt)×cosk(z-x)dk
Вследствие того, что
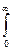 exp (-k2Dt) cos k(z-x) dk =
exp (-k2Dt) cos k(z-x) dk = 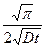 exp(
exp(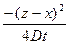 )
)
Получаем
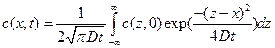 (9)
(9)
Теперь используем граничные условия (4) и (5):
с(x,t)= 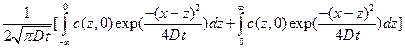 =
=
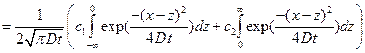 =
=
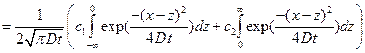 (10)
(10)
Введем обозначение:
y = 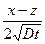 , dy = -
, dy = - 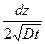 .
.
Тогда
с(z,t) = - 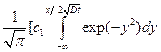 + с2
+ с2 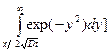 =
=
= - 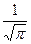 [
[ 
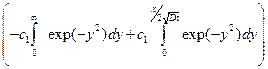 -
-
- 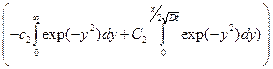 ]
] 
Так как 
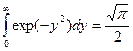 , то
, то
C(x,t) = 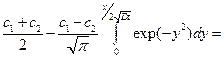
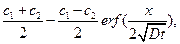 (11)
(11)
где erf z 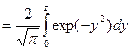 - функция ошибок Гаусса.
- функция ошибок Гаусса.
Теневой метод заключается в измерении смещения светового луча при прохождении через среду с градиентом показателя преломления.
Метод Винера осуществляется следующим образом. При помощи диафрагмы создается узкий пучок света, который проходит через стеклянную кювету с исследуемыми жидкостями. Слой менее плотной жидкости располагается сверху для исключения конвективного движения. Наличие градиента концентрации в кювете вызывает отклонение пучка на некоторый угол 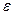 , пропорциональный градиенту показателя преломления (т.к.
, пропорциональный градиенту показателя преломления (т.к. 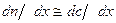 , то
, то 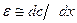 ). Отклонение наблюдается на экране или фотографируется.
). Отклонение наблюдается на экране или фотографируется.
В случае малой ширины стеклянной кюветы можно считать, что траектории лучей проходят через область с постоянным местным градиентом показателя преломления. При малых углах отклонения e траектория луча заменяется дугой окружности радиуса R, который связан с grad r формулой:
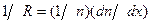
В соответствии с уравнением распространения светового луча, 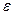 = 1/R. Световой луч дополнительно отклоняется при входе в воздух, поэтому окончательный угол отклонения по закону рефракции Снеллиуса (
= 1/R. Световой луч дополнительно отклоняется при входе в воздух, поэтому окончательный угол отклонения по закону рефракции Снеллиуса (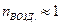 ) равен:
) равен:
sin 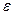 ’/sin
’/sin 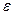 =
= 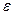 ’/
’/ 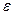 = n
= n
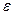 ’ = n
’ = n 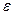 =
= 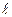 (dn/dx).
(dn/dx).
Когда 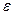 мало, не учитывается также смещение светового луча при прохождении стеклянной стенки кюветы. Решение уравнения Фика (2) для данного случая представляется формулой (11).
мало, не учитывается также смещение светового луча при прохождении стеклянной стенки кюветы. Решение уравнения Фика (2) для данного случая представляется формулой (11).
Поскольку показатель преломления n пропорционален концентрации c, то решение уравнения Фика для n будет иметь следующий вид:
n(x,t) = 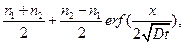 (12)
(12)
Где 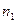 и
и 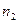 - показатели преломления первой и второй жидкости соответственно. При х=0 и любых значениях t, не равных нулю,
- показатели преломления первой и второй жидкости соответственно. При х=0 и любых значениях t, не равных нулю,
n(0,t) = (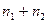 ) / 2
) / 2
В любой момент времени градиент показателя преломления в точке х=0
имеет максимальное значение, равное:
dn/dx = (n2-n1) / 2 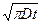 (13)
(13)
максимальный угол отклонения 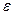 ’ определяется по формуле:
’ определяется по формуле:
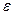 ’=
’= 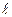 (dn /dx) =
(dn /dx) = 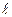 (n2 - n1) / 2
(n2 - n1) / 2 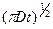 (14)
(14)
в этом случае величина t, обозначающая промежуток времени от начала диффузии до момента наблюдения, при данных условиях трудно поддается точному измерению, и определение коэффициента диффузии из одного наблюдения оказывается неточным. Поэтому необходимо найти величинy 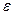 ’ для нескольких различных моментов времени. Для t1 и t2 получим углы отклонения
’ для нескольких различных моментов времени. Для t1 и t2 получим углы отклонения 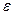 1’ и
1’ и 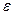 2’:
2’:
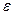 1’ =
1’ = 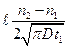 ,
, 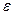 2’ =
2’ = 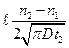 .
.
Отсюда
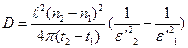 (15)
(15)
В диффузометрах первоначально четкая граница приводимых в соприкосновение жидкостей устанавливается посредством наслоения более легкой из двух жидкостей на более тяжелую или подслаиванием более тяжелой под легкую.
Принципиальная схема метода, применяемого для определения коэффициента диффузии, изображена на рис.1.
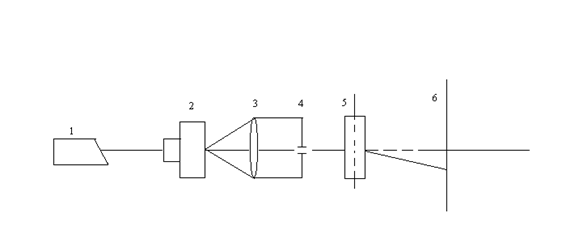
Рис. 1.
Луч лазера 1 проходит через микрообъектив 2, коллиматор 3, диафрагму 4 и диффузионную кювету 5, градиент концентрации в которой направлен по оси х, а затем попадает на экран 6. При наличии градиента показателя преломления 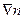 лучи, прошедшие через слой жидкости, отклоняются в сторону увеличения n в тем большей степени, чем выше градиент dn / dx в соответствующем слое.
лучи, прошедшие через слой жидкости, отклоняются в сторону увеличения n в тем большей степени, чем выше градиент dn / dx в соответствующем слое.
По мере протекания процесса диффузии максимальный градиент, а в соответствии с ним и угол отклонения луча 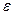 , будет изменяться. Измеряя смещение луча в различные моменты времени после начала диффузии, по формуле (15) рассчитывается коэффициент диффузи.
, будет изменяться. Измеряя смещение луча в различные моменты времени после начала диффузии, по формуле (15) рассчитывается коэффициент диффузи.
Порядок выполнения работы.
1. Соберите оптическую схему, как показано на рис.1, и съюстируйте её, получив на экране тонкий световой пучок.
2. На пути параллельного пучка лучей поставьте на столик диффузионный сосуд и налейте в него до половины воды.
3. Наберите в пипетку раствор поваренной соли известной концентрации и осторожно опустив на дно сосуда, подслаивайте раствор до тех пор, пока луч не пересечет границу раздела двух жидкостей. Зафиксируйте время начала диффузии.
4. Измерьте велечину смещения луча в моменты времени t2 и t1. Вычислите коэффициент диффузии.
Показатель преломления воды n1=1,333, показатель преломления 20% раствора поваренной соли n2=1,364.
Дата добавления: 2015-08-21; просмотров: 120 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Малькольм Дж. Бреарли | | | IV. Аналітичні дані до рахунку N 60 |