Пример математической визуализации с помощью метода COGNISTYLE

Чтобы убедиться в универсальности метода CogniStyle, рассмотрим в качестве примера математическую задачу, а именно: возведение мат­рицы в степень (рис. 140). Особенность задачи в том, что требуется
возвести в степень матрицу частного вида, которая называется сопровождающей матрицей многочлена[30] [14]. Можно показать, что строки искомой матрицы — это векторы, являющиеся коэффициентами многочленов, принадлежащих определенной последовательности многочленов, а сами многочлены (члены последовательности) суть остатки от деления единицы на некоторый многочлен (получаемый путем преобразования нижней строки заданной матрицы), причем деление единицы на многочлен производится, начиная с младших степеней (как при делении рядов) [15]. Впрочем, в данный момент нас интересует не математическая суть вопроса, а конкретный набор эргономических средств и приемов, используемых для описания математической задачи, чтобы сделать ее предельно ясной, доходчивой и легкой для понимания.

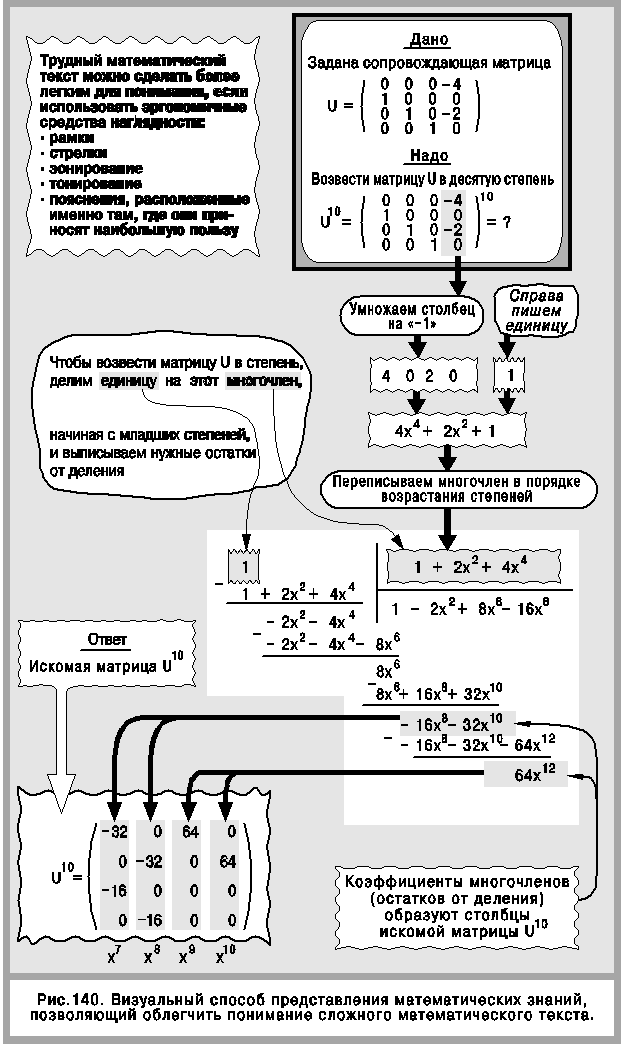
На рис. 140 использованы очень простые, но с эргономической точки зрения весьма выразительные визуальные средства:

! Рамки различной формы, акцентирующие внимание на нужных математических объектах.

! Стрелки, устанавливающие связи между понятиями, заключенными в рамки.

! Стрелки, связывающие пояснения (расположенные в округлых рамках типа “облако”) с нужными понятиями.

! Зонирование текста, т. е. выделение тех или иных фрагментов текста с помощью замкнутых контуров различной формы. Форма контура имеет некоторый алфавит (визуальный синтаксис) и соответствующую визуальную семантику. Зонирование выполняет три функции:

1) четко отделяет математический текст (математические объекты и связанные с ними математические преобразования) от метатекста (словесных пояснений к математическому тексту);

2) организует “статическую” структуру диосцены;

3) вместе со стрелками организует “динамическую” структуру дио­сцены, позволяющую проследить ход математических преобра­зований.

! Тонирование текста с помощью оттенков серого и белого цветов помогает зрительно дифференцировать разные визуально-матема­тические понятия и облегчить зрительное восприятие их иерархи­ческой структуры.

Перечисленные и другие средства позволяют улучшить восприятие математического текста, сократить интеллектуальные усилия, которые человек затрачивает на процесс чтения, понимания и усвоения знаний.

Каждый из названных пунктов представляет некоторый общий эргономический принцип, который может быть детализирован и превращен в большое число конкретных формально-эргономических правил. Впрочем, с математической точки зрения они не являются формальными. Чтобы достичь терминологического компромисса, их можно назвать “полуформальными”.

Таким образом, CogniStyle — это “полуформальный” метод.

Выводы

1. Одной из главных проблем математики является ее неимоверная трудность, которая во многих случаях превышает возможности человеческого ума, что является основной причиной математического терроризма.

2. Сегодня производительность математического труда крайне низка, однако повышение этой производительности есть проблема не столько математики, сколько эргономики.

3. Математическая формализация является — по крайней мере частично — эргономическим процессом, а раз так, ее можно и нужно рас­сматривать с когнитивно-эргономических позиций.

4. Применение когнитивно-эргономических методов для улучшения письменной (визуальной) формы представления математических знаний позволяет существенно улучшить когнитивное качество и понимаемость математических текстов.

5. Традиционные формы и методы развития и фиксации математических идей, игнорирующие эргономические аспекты математических проблем и тем самым создающие питательную среду для математического терроризма, следует признать устаревшими.

6. Для успешного продвижения вперед необходимо осуществить синтез идей математики и эргономики в рамках нового междисциплинарного направления — эргоматематики.

7. В настоящее время имеются все необходимые предпосылки для практического создания нового поколения учебников математики, построенных с учетом когнитивно-эргономических принципов.

8. Цель создания нового поколения математических учебников и книг состоит в том, чтобы сократить интеллектуальные трудозатраты на восприятие, понимание и глубокое усвоение математических знаний в несколько раз, возможно на порядок.

Дата добавления: 2015-08-21