Гиперболические функции

Формула Эйлера позволяет рассматривать в качестве аргумента мнимые величины, например, вместо α рассмотрим jα. Составим два уравнения Эйлера в которых мнимая часть аргумента

принимает положительное и отрицательное значение и решим эти уравнения путем их сложения:

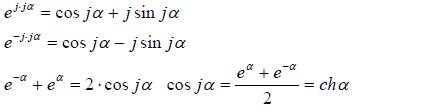
Полученная зависимость говорит о том, что косинус мнимого аргумента образует зависимость, которую называют гиперболическим косинусом.

Если же обе части второго уравнения умножить на -1, получим новую систему уравнений, которую также решим путем сложения:

Из полученной формулы следует, что синус мнимого аргумента образует зависимость, которую называют гиперболическим синусом (зависимость, стоящая после мнимой единицы).

При решении уравнений учитывалось, что знак синуса зависит от знака аргумента, функция нечетная, знак косинуса не зависит от знака аргумента – функция четная.

По аналогии с обычными тригонометрическими функциями можно образовать и другие гиперболические функции:

При использовании гиперболических функций несколько расширяется понятие аргумента, а именно, вместо понятия угла для обычной тригонометрической функции вводится понятие обобщенного аргумента, изменяющегося от -∞ до +∞., причем аргумент может быть как действительным числом, так и мнимым, а даже комплексным.

Гиперболические функции описывают параметры длинных линий электропередачи, что будет показано в следующих разделах, причем аргументы будут использоваться в самом общем виде.

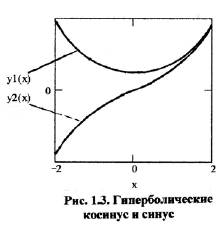
На рис. 1.3 изображены графики гиперболических синуса (у2(х)) и косинуса (у1(х)). Косинус имеет вид гиперболы (существует строгое доказательство, что это именно гипербола), причем значение функции не снижается ниже +1 и с ростом аргумента устремляется в бесконечность. Гиперболический синус изменяется от минус бесконечности до плюс бесконечности. Таким образом, гиперболический косинус является четной функцией, а гиперболический синус нечетной функцией.

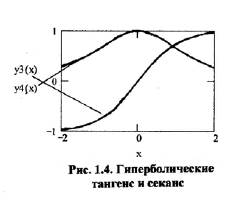
Следующий график (рис. 1.4) показывает следующие две зависимости, y3(x) – гиперболический тангенс и y4(x) – гиперболический секанс. Нетрудно заметить, что тангенс по абсолютной величине не превышает 1 при увеличении аргумента. Гиперболический секанс также не превышает единицы, но все его значения находятся в положительной области. При увеличении аргумента как в сторону отрицательных значений, так и положительных гиперболический секанс стремится к нулю. Из изложенного следует, что гиперболический тангенс является нечетной функцией, а гиперболический секанс четной функцией.

Две последние функции представлены на рис. 1.5, у5(х) - гиперболический котангенс, у6(х) – гиперболический косеканс. Однако на данном диапазоне аргументов эти две функции на графике практически неотличимы. Отличие начинается при больших значениях аргумента, причем с ростом аргумента гиперболический котангенс стремится к единице, а гиперболический косеканс стремится к нулю.

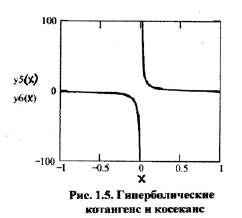
Из анализа графика рис. 1.5 следует, что обе функции нечетные, их знак зависит от знака аргумента.

Гиперболические функции находят широкое применение при использовании электромагнитных процессов в длинных линиях электропередачи и при составлении их математических моделей.

Дата добавления: 2015-08-21