Линейные дифференциальные уравнения 1-го и 2-го порядка

Линейные дифференциальные уравнения первого порядка с постоянными коэффициентами. Различают два вида таких уравнений: однородные, у которых правая часть равна нулю, и неоднородные, содержащие правую часть. Рассмотрим однородные уравнения. В общем виде они выглядят следующим образом:

Здесь а и b – постоянные коэффициенты. Это уравнение, вообще говоря, относится к уравнениям с разделяющимися переменными. Разделим почленно на U(x) и умножим на dx, получим решение:

Постоянная интегрирования С находится из начальных условий.Рассмотрим пример. На электрическую цепь (рис.4.1),

,состоящую из резистора с сопротивлением R и конденсатора емкостью С, включением ключа В подается синусоидальное напряжение Еm·sin(ω·t + φ), где ω –угловая частота, φ – угол, определяющий момент подачи напряжения. В результате имеет место электромагнитный переходный процесс, который характеризуется изменяющимся во времени токомi(t) и напряжением u(t). Требуется определить зависимость этих величин от времени. Из электротехники известно, что такой переходный процесс описывается интегральным уравнением:

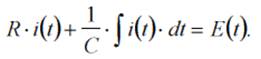
В практических расчетах чаще всего

E(t) - периодическая функция времени.

Дифференцируя получаем дифференциальное уравнение первого порядка:

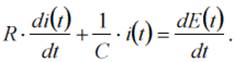
Преобразуем уравнение, разделив обе его части на R и обозначив производную подаваемого напряжения как ξ(t). Кроме того, произведение R·C = T представляет собой постоянную времени схемы. получаем новую форму:

Характеристическое уравнение, его решение и решение однородной части:

Производная подаваемого напряжения:

Находим решение уравнения:

Интеграл табличный:

Подстановка полученного интеграла дает следующее значение тока:

Постоянная интегрирования А находится из следующих соображений. При

t = 0 интеграл в формула равен нулю, поскольку пределы интегрирования одинаковые. Кроме того, принимаем, что конденсатор перед подачей напряжения разряжен. В момент подачи напряжения сопротивление конденсатора равно нулю, отсюда следует:

Результат получается несколько громоздким, поэтому особой необходимости расписывать его нет.

Дифференциальные уравнения второго порядка с постоянными коэффициентами. Они имеют широкое применение при анализе электромагнитных и электромеханических переходных процессах в электроэнергетических системах. Общий вид таких уравнений следующий:

Также, как и в случае уравнений первого порядка, различают уравнения однородные и неоднородные.

Однородное уравнение:

Неоднородные уравнения решаются в два этапа. На первом этапе решается однородная часть уравнения. На втором этапе предполагается, что коэффициенты есть функции аргумента х и их значение требуется определить.

Учитывая, что напряжение на конденсаторе есть интегральная функция от времени, имеем:

Дифференцируя это уравнение, получаем дифференциальное уравнение второго порядка:

Дата добавления: 2015-08-21