Основні поняття та теореми диференціального числення.

КУРСОВА РОБОТА

Застосування диференціального числення до наближеного розв’язку транциндентних рівнянь

Виконала

ст. групи 4211-1 А.В. Чулкова

(шифр) (підпис і дата) (ім’я, по батькові, прізвище)

Керівник Ю.М.Стреляєв

(підпис і дата) (ім’я, по батькові, прізвище)

Запоріжжя

План

Основні поняття та теореми диференціального числення.

Диференціальне числення – розділ математики, в якому вивчаються похідні, диференціали та їх застосування в дослідженні властивостей функцій. Формування диференціального числення пов'язано з іменами Ісака Ньютона та Ґотфріда Лейбніца. Саме вони чітко сформували основні положення та вказали на взаємообернений характер диференціювання та інтегрування. Створення диференціального числення (разом з інтегральним) відкрило нову епоху розвитку математики. З цим пов'язані такі дисципліни як теорія рядів, теорія диференціальних рівнянь та багато інших. Методи математичного аналізу знайшли використання у всіх розділах математики. Дуже поширилася область застосування математики у природничих науках та техніці.

Основна ідея диференціального числення складається у вивченні функції у малому. Точніше диференціальне числення дає апарат для дослідження функцій, поведінка яких у досить малому околі кожної точки близька до поведінки лінійної функції чи многочлена. Таким апаратом слугують центральні поняття диференціального числення: похідна і диференціал.

Похідна́ — основне поняття диференційного числення, що характеризує швидкість зміни функції. Визначається як границя відношення приросту функції до приросту її аргументу коли приріст аргументу прямує до нуля (якщо така границя існує). Функцію, що має скінченну похідну, називають диференційованою.

Визначення: Нехай в деякому околі точки x₀ визначена функція . Якщо ми візьмемо довільне число 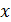в цьому околі, то приріст аргументу (позначається ) в цьому випадку визначається, як 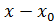, а приріст функції () — як Тоді, якщо існує границя , то вона називається похідною функції в точці .

Похідною функцією даної функції називається функція, що в будь-якій точці області визначення дорівнює похідній даної функції в цій точці.

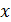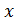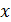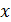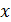Диференціювання – це метод обчислення співвідношення приросту залежної змінної по відношенню до приросту незалежної змінної . Це співвідношення приростів називається похідною функції по змінній . Якщо говорити більш точно, залежність від означає, що функція від Ця функціональна залежність часто позначається , де позначає функцію. Якщо та дійсні числа, і якщо графік функції зображено відносно , похідна дорівнює нахилу дотичної до цього графіка в кожній точці.

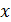Найпростіший випадок коли – лінійна функція від , це означає що графік функції відносно 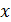пряма лінія. В такому випадку, , для дійсних чисел та 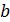, і нахил визначається так

де символ Δ (грецька літера у верхньому регістрі дельта) – це є скорочення для "зміни в". Ця формула справедлива тому, що

.

З цього випливає, що

Отримали точне значення нахилу прямої лінії. Якщо функція ƒ не лінійна (тобто графік функції не пряма лінія), тоді приріст поділений на приріст змінюється: диференціювання це спосіб обчислення точного значення відношення приростів для будь-якого значення

Ідея полягає в тому, щоб обчислити відношення приростів як граничну величину коли 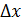стає нескінченно малим.

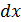Якщо використати позначення Лейбніца, тоді нескінченно малий приріст позначається як , а похідна функції по змінній 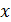записується:

виглядає як відношення двох нескінченно малих величин. (Цей вираз читається так: "похідна функції по змінній 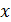"або " по dx").

Геометричний зміст похідної: Значення похідної функції у точці дорівнює значенню кутового коефіцієнта дотичної до кривої у точці з абсцисою .

Рівняння дотичної до кривої у точці має вигляд:

Дата добавления: 2015-08-21