
|
Читайте также: |
1 метод хорд:
Нехай знайдено початковий інтеграл  , в якому лежить тільки один простий корінь рівняння
, в якому лежить тільки один простий корінь рівняння  та виконані умови
та виконані умови  .Розглянемо графік функції
.Розглянемо графік функції  . Нехай
. Нехай  ,
,  .
.
Проведемо хорду, яка проходить через  та
та 
 /
/
Запишемо рівняння хорди АВ:

За наближене значення шуканого кореня приймемо абсцису 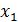 точки перетину хорди АВ з віссю
точки перетину хорди АВ з віссю  . Тобто, якщо покласти
. Тобто, якщо покласти  та
та  ,маємо
,маємо
 *
* 
Це дає нам перше наближення кореня 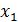 - перетин хорди з віссю O
- перетин хорди з віссю O 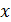 . Далі будуємо хорди до того з відрізків
. Далі будуємо хорди до того з відрізків  або
або  , на кінцях якого функція має протилежні знаки, отримаємо друге наближення
, на кінцях якого функція має протилежні знаки, отримаємо друге наближення  і т.д.
і т.д.
Для збіжності процесу необхідно, щоб друга похідна  зберігала знак на відрізку
зберігала знак на відрізку  .Нехай, наприклад,
.Нехай, наприклад,  . Тоді крива буде опуклою вниз,а це означає, що вона розташована нище своєї хорди АВ. Можливі два випадки: 1)
. Тоді крива буде опуклою вниз,а це означає, що вона розташована нище своєї хорди АВ. Можливі два випадки: 1)  та 2)
та 2)  .У першому випадку кінець
.У першому випадку кінець  нерухомий, а початкове наближення
нерухомий, а початкове наближення  .У другому – нерухомий кінець
.У другому – нерухомий кінець 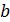 ,а початкове наближення
,а початкове наближення  .Тому нерухомий той кінець,для якого знак функції
.Тому нерухомий той кінець,для якого знак функції  співпадає зі знаком її другої похідної
співпадає зі знаком її другої похідної  .
.
Нехай в якості нерухомого кінця буде  , тоді:
, тоді:
Якщо  , то покласти
, то покласти  ;
;
Якщо  , то покласти
, то покласти  ;
;
Наступні наближені значення кореня знаходимо за формулою
 ,
, 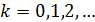
Послідовність чисел  прямує до шуканого кореня рівняння
прямує до шуканого кореня рівняння  . Обчислення наближених значень кореня слід проводити, поки не буде досягати задана точність
. Обчислення наближених значень кореня слід проводити, поки не буде досягати задана точність  А саме,ітераційний процес завершуємо, якщо
А саме,ітераційний процес завершуємо, якщо  і за наближене значення кореня приймає
і за наближене значення кореня приймає 
Метод дотичних (Ньютона)
Нехай знайдено початковий інтеграл  в я кому лежить тільки один простий корінь рівняння
в я кому лежить тільки один простий корінь рівняння  та виконані умові
та виконані умові  . Причому
. Причому 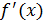 та
та  - неперервні та зберігають знаки
- неперервні та зберігають знаки  .В якості
.В якості  вибирають той кінець інтервалу
вибирають той кінець інтервалу  ,для якого
,для якого  .Виберемо
.Виберемо  та проведемо дотичну до кривої
та проведемо дотичну до кривої  в точці
в точці 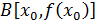

У якості першого першого наближення 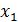 кореня приймаємо абсцису точки перетину цієї дотичної з віссю
кореня приймаємо абсцису точки перетину цієї дотичної з віссю  .Через точку
.Через точку  проводимо дотичну, абсциса точки перетину якої знов дає нам друге наближення
проводимо дотичну, абсциса точки перетину якої знов дає нам друге наближення  кореня і т.д. Рівняння дотичної в точці
кореня і т.д. Рівняння дотичної в точці 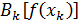
 має вигляд
має вигляд
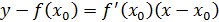
Якщо покласти  , отримаємо ітераційну формулу
, отримаємо ітераційну формулу
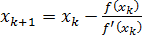 ,
, 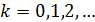
Якщо задана точність обчислень  , то ітераційний процес завершуємо, коли
, то ітераційний процес завершуємо, коли  а за наближене значення кореня приймаємо
а за наближене значення кореня приймаємо  .
.
Метод простої ітерації
Щоб знайти корені рівняння  замінимо його рівносильним
замінимо його рівносильним  Виберемо початкове наближення
Виберемо початкове наближення  і послідовно обчислимо наближення
і послідовно обчислимо наближення

Збіжність послідовності  забезпечується відповідним вибором функції
забезпечується відповідним вибором функції  і початкового наближення
і початкового наближення 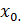 Нехай
Нехай  - корінь рівняння
- корінь рівняння  який належить відрізку
який належить відрізку  . Якщо
. Якщо 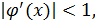 для
для  , то послідовність
, то послідовність  збігається до кореня
збігається до кореня  . Якщо задана точність обчислень
. Якщо задана точність обчислень  то ітераційний процес завершуємо, якщо
то ітераційний процес завершуємо, якщо  , а за наближене значення кореня приймаємо
, а за наближене значення кореня приймаємо 
Дата добавления: 2015-08-21; просмотров: 85 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Основні поняття та теореми диференціального числення. | | | Ганс Андерсен |