
Читайте также:
|
Формальная арифметика получается из теории с равенством добавлением константы 0, введением функциональных символов. f(x,y) = x + y, g(x,y) = xy, next(x) = x’ и добавлением следующих собственных аксиом: (Ar1) F(0)  (
( х (F(x)
х (F(x)  F(x’))
F(x’)) 
 x F(x)), (Ar2) (t’1 = t’2)
x F(x)), (Ar2) (t’1 = t’2)  (t1= t2), (Ar3) (t1 = t2 )
(t1= t2), (Ar3) (t1 = t2 )  (t’1= t’2), (Ar4) t’
(t’1= t’2), (Ar4) t’  0, (Ar5) t + 0 = t’, (Ar6) t1 + t’2 = (t1 + t2)’, (Ar7) t·0 = 0, (Ar8) t1· t’2 = t1 · t2 + t1. Аксиому Ar1 называют принципом математической индукции. Приведем другую формулировку этого принципа. Свойство 1. Если ⊢ F(0) и ⊢ F(x)
0, (Ar5) t + 0 = t’, (Ar6) t1 + t’2 = (t1 + t2)’, (Ar7) t·0 = 0, (Ar8) t1· t’2 = t1 · t2 + t1. Аксиому Ar1 называют принципом математической индукции. Приведем другую формулировку этого принципа. Свойство 1. Если ⊢ F(0) и ⊢ F(x)  F(x)’, то ⊢
F(x)’, то ⊢  х F(x). Доказательство состоит из следующих утверждений: 1) ⊢ F(x)
х F(x). Доказательство состоит из следующих утверждений: 1) ⊢ F(x)  F(x)’ – дано по условию; 2) ⊢
F(x)’ – дано по условию; 2) ⊢  х(F(x)
х(F(x)  F(x’)) – из 1) по правилу обобщения; 3) ⊢F(0) – дано по условию; 4) ⊢F(0)
F(x’)) – из 1) по правилу обобщения; 3) ⊢F(0) – дано по условию; 4) ⊢F(0)  (
( F(x)
F(x)  F(x’))
F(x’)) 
 x F(x)) – аксиома Ar1, 5) ⊢
x F(x)) – аксиома Ar1, 5) ⊢  x (F(x)
x (F(x)  F(x’))
F(x’)) 
 x F(x) – из 3) и 4) по правилу MP, 6) ⊢
x F(x) – из 3) и 4) по правилу MP, 6) ⊢  x F(x) – из 2) и 5) по правилу MP. Свойство 1 доказано. Моделью для формальной арифметики является множество Nu обычными операциями сложения и умножения, а next(x) = х + 1. В отличие от исчисления высказываний и исчисления предикатов формальная арифметика не является полной. Мы приведем без доказательства формулировки теоремы о ее неполноте. Теорема Геделя о неполноте. Существует замкнутая формула F такая, что в формальной арифметике не выводиться как формула F, так и ее отрицание
x F(x) – из 2) и 5) по правилу MP. Свойство 1 доказано. Моделью для формальной арифметики является множество Nu обычными операциями сложения и умножения, а next(x) = х + 1. В отличие от исчисления высказываний и исчисления предикатов формальная арифметика не является полной. Мы приведем без доказательства формулировки теоремы о ее неполноте. Теорема Геделя о неполноте. Существует замкнутая формула F такая, что в формальной арифметике не выводиться как формула F, так и ее отрицание  .
.
1.19. дать определение дизьюнкции, коньюнкции и отрицания в нечеткой логике. доказать в нечеткой логике, что a v (b  с) = (а V b) ∧ (a V c) и
с) = (а V b) ∧ (a V c) и  =
=  V
V  . В нечеткой логике рассматриваются функции у=f(x1,…, xn),где Xi
. В нечеткой логике рассматриваются функции у=f(x1,…, xn),где Xi  [0;1] при i= 1,2, …., n и у
[0;1] при i= 1,2, …., n и у  [0;1]. Определение 1. Значения нечеткой дизьюнкции и коньюкции определяется по формуле у= х1Vх2=max(x1,x2) и у = x1∧x2= min(x1,x2). Следующие свойства нечеткой дизьюнкции и коньюнкции такие же, как и для двузначной логики: 1)a V 0 = a; 1’) a ∧ 0 = 0; 2) a V 1 = 1; 2’) a ∧ 1 = a; 3) a V a = a; 3’) a ∧ a = a; 4) a V b = b V a; 4’) a ∧ b = b ∧ a; 5) a V (b V c) = (a V b) V c; 5’) a∧ (b ∧ c) = (a ∧ b) ∧ c; 6) если a
[0;1]. Определение 1. Значения нечеткой дизьюнкции и коньюкции определяется по формуле у= х1Vх2=max(x1,x2) и у = x1∧x2= min(x1,x2). Следующие свойства нечеткой дизьюнкции и коньюнкции такие же, как и для двузначной логики: 1)a V 0 = a; 1’) a ∧ 0 = 0; 2) a V 1 = 1; 2’) a ∧ 1 = a; 3) a V a = a; 3’) a ∧ a = a; 4) a V b = b V a; 4’) a ∧ b = b ∧ a; 5) a V (b V c) = (a V b) V c; 5’) a∧ (b ∧ c) = (a ∧ b) ∧ c; 6) если a  b, то a V c
b, то a V c  b V c; 6’) если a
b V c; 6’) если a  b, то a ∧ c
b, то a ∧ c  b ∧ c; 7)a ∧ (b V c) = (a ∧ b) V (a ∧ c); 7’) a V (b ∧ c) = (a V b) ∧ (a ∧ c). Свойства 1 – 6 и 1’ – 6’ непосредственно вытекают из определения: приведем доказательство свойства 7. Пусть b
b ∧ c; 7)a ∧ (b V c) = (a ∧ b) V (a ∧ c); 7’) a V (b ∧ c) = (a V b) ∧ (a ∧ c). Свойства 1 – 6 и 1’ – 6’ непосредственно вытекают из определения: приведем доказательство свойства 7. Пусть b  c, тогда a ∧ (b V c) = a ∧ c и (a ∧ b) V (a ∧ c) = a ∧ c, т.к. a ∧ b
c, тогда a ∧ (b V c) = a ∧ c и (a ∧ b) V (a ∧ c) = a ∧ c, т.к. a ∧ b  a ∧ c по свойству 6’. Свойство 7’ доказывается аналогично. Определение 2. Значение нечеткого отрицания определяется по формуле у=
a ∧ c по свойству 6’. Свойство 7’ доказывается аналогично. Определение 2. Значение нечеткого отрицания определяется по формуле у=  =1- х. Следующие св-ва нечеткого отрицания совпадают со свойствами отрицания в двузначной логике: 1)
=1- х. Следующие св-ва нечеткого отрицания совпадают со свойствами отрицания в двузначной логике: 1)  = 1, 2)
= 1, 2)  = 0, 3)
= 0, 3)  = a, 4)
= a, 4)  a
a  b, то
b, то 

 , 5)
, 5)  =
=  ∨
∨  , 6)
, 6)  =
=  ∧
∧  Доказательство свойств 8 – 11 очевидно; докажем свойство 12. Пусть a
Доказательство свойств 8 – 11 очевидно; докажем свойство 12. Пусть a  b, тогда
b, тогда  =
=  , так как a ∧ b = a; a
, так как a ∧ b = a; a  ∨
∨  =
=  потому, что
потому, что 
 b. Св-во 13 доказывается аналогично. Определение 3. Функция у = х ∧
b. Св-во 13 доказывается аналогично. Определение 3. Функция у = х ∧  называется противоречием, обозначается у =
называется противоречием, обозначается у =  . Из этого определения вытекают следующие св-ва:
. Из этого определения вытекают следующие св-ва:  =
=  15)
15)  Определение 4. Функция у = х ∨
Определение 4. Функция у = х ∨  называется тавтологией, обозначается у =
называется тавтологией, обозначается у =  . Из этого определения вытекает следующие св-ва:
. Из этого определения вытекает следующие св-ва:  =
=  17)
17) 
 Заметим, что в двузначной логике х ∧
Заметим, что в двузначной логике х ∧ 
 0, а х V
0, а х V 
 1, что не имеет места в нечеткой логике. Определение 5. Функция у = f(х) называется противоречивой, если f(х)
1, что не имеет места в нечеткой логике. Определение 5. Функция у = f(х) называется противоречивой, если f(х)  для всех х
для всех х  Примером противоречивой функции является у =
Примером противоречивой функции является у =  . Определение 6. Функция у = f (х) называется общезначимой, если f (х)
. Определение 6. Функция у = f (х) называется общезначимой, если f (х) 
 для всех х
для всех х  . В качестве примера общезначимой функции можно привести тавтологию у =
. В качестве примера общезначимой функции можно привести тавтологию у =  .
.
1.20. Дать определение нечеткой импликации и эквивалентности. Доказать в нечеткой логике, что a  b = (a ∧ b) V (
b = (a ∧ b) V (  ∧
∧  ). Определение 1. Нечеткая импликация определяется по формуле а
). Определение 1. Нечеткая импликация определяется по формуле а  b =
b =  V b. Из этого определения вытекают следующие свойства: 1) 0
V b. Из этого определения вытекают следующие свойства: 1) 0  a = 1, 2) a
a = 1, 2) a  1 = 1, 3) a
1 = 1, 3) a  a =
a =  ∨ a =
∨ a =  Определение 2. Нечеткую эквиваленцию можно определить по формуле а
Определение 2. Нечеткую эквиваленцию можно определить по формуле а  b = (a
b = (a  b) ∧ (
b) ∧ (
 a). Отметим следующие св-ва нечеткой эквиваленции: a
a). Отметим следующие св-ва нечеткой эквиваленции: a  b = (
b = ( ∨ b) ∧ (
∨ b) ∧ ( ∨ a), a
∨ a), a  a =
a =  V a =
V a =  , a
, a  b = (a ∧ b) ∨ (
b = (a ∧ b) ∨ ( ∧
∧  ). Докажем свойство 6. Для этого разберем два случая. 1) Пусть a
). Докажем свойство 6. Для этого разберем два случая. 1) Пусть a 
 , тогда
, тогда 
 b, из них выводится, что
b, из них выводится, что  ∧ b) ∧ (a ∨
∧ b) ∧ (a ∨  ) =
) =  ∧
∧  ⟹ a
⟹ a  b =
b =  ∧
∧  . С другой стороны,
. С другой стороны,  ∧
∧  ⟹ (a ∧ b) ∨ (
⟹ (a ∧ b) ∨ ( ∧
∧  ) =
) =  ∧
∧  , следовательно, a
, следовательно, a  = (a ∧ b) V (
= (a ∧ b) V ( ∧
∧  ). 2) Случай a
). 2) Случай a 
 разбирается аналогично. Замечание. Можно ввести в нечеткой логике и остальные логические операции по формулам х ⊕ у =
разбирается аналогично. Замечание. Можно ввести в нечеткой логике и остальные логические операции по формулам х ⊕ у =  – “ исключающие или “, х ⎡у =
– “ исключающие или “, х ⎡у =  ∨
∨  - штрих Шеффера, х ↓у =
- штрих Шеффера, х ↓у =  ∧
∧  - стрелка Пирса.
- стрелка Пирса.
1.21. Дать определение нечеткого множества и операций дополнения, пересечения, объединения, возведения в степень, умножения и сложения нечетких множеств. Доказать, что A  B ⊂ A + B.
B ⊂ A + B.
Нечеткое значение высказывания Р будем обозначать µ(Р). Определение 1. Множество А называется нечетким, если задана функция принадлежности, которая по любому его элементу х определяет число µА(х) = µ(х  [0;1], равное нечеткому значению предиката х
[0;1], равное нечеткому значению предиката х  U\ А, где U – универсум, считается по умолчанию, что µА(х) = 0. Пример 1. Зададим нечеткие множества А и В таким образом: А =
U\ А, где U – универсум, считается по умолчанию, что µА(х) = 0. Пример 1. Зададим нечеткие множества А и В таким образом: А =  /х1, 1/х2, 0.8/х3, 0/х4
/х1, 1/х2, 0.8/х3, 0/х4  , В =
, В =  ; из этой записи следует, что µА(х1) = 0.3, µА(х2) =1, µВ(х1) = 0 и т.д.. Определение 2. Для нечетких множеств можно определить отношения равенства и подмножества: А = В, если
; из этой записи следует, что µА(х1) = 0.3, µА(х2) =1, µВ(х1) = 0 и т.д.. Определение 2. Для нечетких множеств можно определить отношения равенства и подмножества: А = В, если  х(µА(х) = µВ(х)); А ⊂ В, если
х(µА(х) = µВ(х)); А ⊂ В, если  х(µА(х)
х(µА(х)  µВ(х)). Заметим, что, если
µВ(х)). Заметим, что, если  х(µА(х) = 0), то множество А считается пустым, А = ∅. Определение 3. Функции принадлежности для дополнения, пересечения и объединения нечетких множеств определяется так:
х(µА(х) = 0), то множество А считается пустым, А = ∅. Определение 3. Функции принадлежности для дополнения, пересечения и объединения нечетких множеств определяется так:  (х)=
(х)= 
 1-
1-  (х),
(х),  =
= 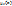 ∧
∧  = min (
= min ( ,
, 
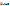 (x) =
(x) =  V
V  (x) = max (
(x) = max ( (x),
(x),  (x)). Из определений 2, 3 и свойств отрицания, коньюнкции и дизьюнкции следует, что на нечеткие множества переносятся обычные свойства операций дополнения, пересечения и объединения. Отметим некоторые из этих свойств. 1) А
(x)). Из определений 2, 3 и свойств отрицания, коньюнкции и дизьюнкции следует, что на нечеткие множества переносятся обычные свойства операций дополнения, пересечения и объединения. Отметим некоторые из этих свойств. 1) А  А = А. 1’) A
А = А. 1’) A  A = A. 2) А
A = A. 2) А  (В
(В  С) = (А
С) = (А  В)
В)  (А
(А  С). 2’) A
С). 2’) A  (B
(B  C) = (A
C) = (A  )
)  (A
(A  C). 3)
C). 3)  =
= 

 . 3’)
. 3’) 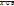 =
= 

 . Определение 4. Введем операции возведения в степень, умножения и сложения нечетких множеств, задавая их функции принадлежности таким образом:
. Определение 4. Введем операции возведения в степень, умножения и сложения нечетких множеств, задавая их функции принадлежности таким образом:  (x) =
(x) =  (x) при n
(x) при n  0,
0,  (x) =
(x) =  (x) ·
(x) ·  (x),
(x),  (x) =
(x) =  (x) +
(x) +  (x) -
(x) -  (x) ·
(x) ·  (x). Отметим некоторые свойства введенных операций. 1)
(x). Отметим некоторые свойства введенных операций. 1)  ⊂ A при n
⊂ A при n  1. 1’) A ⊂
1. 1’) A ⊂  при n
при n  1. 2)
1. 2)  ·B ⊂ A
·B ⊂ A  B. 2’) A
B. 2’) A  B ⊂ A + B. 3)
B ⊂ A + B. 3)  =
=  +
+  . 3’)
. 3’)  =
=  ·
·  . Пример 2. Если А и В – множества, данные в примере 1, то А
. Пример 2. Если А и В – множества, данные в примере 1, то А  В =
В =  А
А  В =
В =  ,
,  =
= 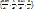 А· В =
А· В =  ,А+В =
,А+В =  Пример 3. Пусть нечеткие значения предикатов р = (х
Пример 3. Пусть нечеткие значения предикатов р = (х  А), q= (x
А), q= (x  B) и r = (x
B) и r = (x  C) следующие: р = 0,2, q = 0,4 и r = 0,7. Найти нечеткое значение предиката s = (x
C) следующие: р = 0,2, q = 0,4 и r = 0,7. Найти нечеткое значение предиката s = (x 
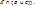 Решение. Поскольку s =
Решение. Поскольку s =  ∧ (q V r), то подставляя значения p,q,r, получаем, что s = 0,8 ∧ (0,4V0,7) = 0,8 ∧ 0,7 = 0,7. Ответ. Нечеткое значение предиката s равно 0,7.
∧ (q V r), то подставляя значения p,q,r, получаем, что s = 0,8 ∧ (0,4V0,7) = 0,8 ∧ 0,7 = 0,7. Ответ. Нечеткое значение предиката s равно 0,7.
Дата добавления: 2015-08-21; просмотров: 58 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Сформулировать и доказать теорему о полноте исчисления высказываний. | | | ЗАДАНИЕ 1 |