
Читайте также:
|
Теорема: Если  , то в исчислении высказываний
, то в исчислении высказываний 
 . Доказательство: Поскольку
. Доказательство: Поскольку  , то по лемме
, то по лемме  при любых значениях σ1,σ2,…,σn.Если σ1=1, то
при любых значениях σ1,σ2,…,σn.Если σ1=1, то  , а при σ1=0 мы имеем что
, а при σ1=0 мы имеем что  . Гипотеза
. Гипотеза  оказывается не существенной, и, удаляя её по теореме мы получаем, что
оказывается не существенной, и, удаляя её по теореме мы получаем, что  . Удаляя тем же образом по очереди все остальные гипотезы, видим что
. Удаляя тем же образом по очереди все остальные гипотезы, видим что 
 .
.
1.11. Правило резолюций. Метод резолюций в ИВ. В двузначной логике имеет место формула: (xvy)( vz)=(xvy)(
vz)=(xvy)( vz) (yvz)-резольвента. Th о методе резолюций в ИВ: Из F1,F2,…,Fn├F↔ F1,F2,…,Fn,
vz) (yvz)-резольвента. Th о методе резолюций в ИВ: Из F1,F2,…,Fn├F↔ F1,F2,…,Fn,  ≡0, F1,F2,…,Fn├F↔├F1→(F2→…(Fn→F)…)↔F1→(F2→…→(Fn→F)…)≡1↔
≡0, F1,F2,…,Fn├F↔├F1→(F2→…(Fn→F)…)↔F1→(F2→…→(Fn→F)…)≡1↔  v
v  v…v
v…v  vF≡1↔
vF≡1↔  ≡0↔F1,F2,…,Fn
≡0↔F1,F2,…,Fn  ≡0.
≡0.
1.12. Некаузальное правило резолюции. Th:Если дана A(x)  B(x)=A(x)
B(x)=A(x)  B(x)
B(x)  (A(0)
(A(0)  B(1)). Разбор случаев по x: x=0 LP=A(0)
B(1)). Разбор случаев по x: x=0 LP=A(0)  B(0). RP=A(0)
B(0). RP=A(0)  B(0)
B(0)  (A(0)
(A(0)  B(1))=A(0)
B(1))=A(0)  B(0)
B(0)  A(0)
A(0)  B(0)
B(0)  B(1)=A(0)
B(1)=A(0)  B(0)
B(0)
1.13. Исчисление предикатов: Опр: Для исчисления предикатов необходимо задать: 1) Алфавит: x1,x2…xn-предметные переменные,  –функциональная переменная, a1,a2…an-предметные постоянные, →,┐,(,),
–функциональная переменная, a1,a2…an-предметные постоянные, →,┐,(,),  -дополнительные символы. 2) Термы: xi,ai-термы. Если
-дополнительные символы. 2) Термы: xi,ai-термы. Если  -функц.переменная, то
-функц.переменная, то  (t1,t2…tn)-терм,где ti-термы. 3) Формулы: Если t1,…,tn термы, то
(t1,t2…tn)-терм,где ti-термы. 3) Формулы: Если t1,…,tn термы, то  (t1,t2…tn)-формула. Если F1 и F2 формулы, то
(t1,t2…tn)-формула. Если F1 и F2 формулы, то  1,
1,  2,F1→F2-ф-лы. Если F(x)-формула, то
2,F1→F2-ф-лы. Если F(x)-формула, то  x F(x),
x F(x),  x F(x) – формулы..
x F(x) – формулы..  предметная переменная x может входить в формулу свободно или связанно. В термах все входящие переменные являются свободными. В ф-ле
предметная переменная x может входить в формулу свободно или связанно. В термах все входящие переменные являются свободными. В ф-ле  (t1,…,tn) все переменные являются свободными. Пишем F(x) если x входит в F свободно. Кванторы связности переменных, т.е.
(t1,…,tn) все переменные являются свободными. Пишем F(x) если x входит в F свободно. Кванторы связности переменных, т.е.  xF(x) x-связ.
xF(x) x-связ.  xF(x)x-связ. 4) Аксиомы: A1,A2,A3 – аксиомы в ИВ, P1=
xF(x)x-связ. 4) Аксиомы: A1,A2,A3 – аксиомы в ИВ, P1=  xF(x)→F(t) где t-переменная, P2=F(t)→
xF(x)→F(t) где t-переменная, P2=F(t)→  xF(x). 5) Правило вывода MP:
xF(x). 5) Правило вывода MP:  где А и В – ф-лы.
где А и В – ф-лы.  - I
- I  , где G -
, где G -  формула не зависящая от x.
формула не зависящая от x.  - I
- I 
1.14. Теорема о подстановке терма и теорема о переименовании связанной переменной. Th1: В ИП  F(x)=>
F(x)=>  F(t), где t-терм. 1)
F(t), где t-терм. 1)  F(x) дано; 2) Let
F(x) дано; 2) Let  G не зависит от x; 3)
G не зависит от x; 3)  F(x)→(G→F(x)) акс A1; 4)
F(x)→(G→F(x)) акс A1; 4)  G→F(x) (MP к 1 и 3); 5)
G→F(x) (MP к 1 и 3); 5)  G→
G→  xF(x) правило введения квантора всеобщности; 6)
xF(x) правило введения квантора всеобщности; 6)  xF(x) (MP к 2 и 5); 7)
xF(x) (MP к 2 и 5); 7)  xF(x)→F(t) акс P1; 8)
xF(x)→F(t) акс P1; 8)  F(t) (MP к 6 и 7); Th2: О переименовании связ.переменных
F(t) (MP к 6 и 7); Th2: О переименовании связ.переменных  xF(x)=>
xF(x)=>  AyF(y); 1)
AyF(y); 1)  xF(x) – дано; 2)
xF(x) – дано; 2)  xF(x)→F(y) акс P1; 3)
xF(x)→F(y) акс P1; 3)  xF(x)→
xF(x)→  yF(y) I
yF(y) I  (2); 4)
(2); 4)  yF(y) (MP к 1 и 3).
yF(y) (MP к 1 и 3).
1.15. Интерпретация и непротиворечивость ИП. При интерпретации ИП задается некоторое множество M. При этом предметная постоянная ai  M, предметная переменная xi
M, предметная переменная xi  M; Ф-ии y=f(x1,…xn) рассмотрим на M xi,y
M; Ф-ии y=f(x1,…xn) рассмотрим на M xi,y  M; Предикатным символам P отвечают предикаты на M: y=P(xi,…xn) xi
M; Предикатным символам P отвечают предикаты на M: y=P(xi,…xn) xi  M, y
M, y  {0;1} =>
{0;1} =>  терм принимает значения в M.
терм принимает значения в M.  ф-ла ИП становится формулой 2-значной логики. Th: Если
ф-ла ИП становится формулой 2-значной логики. Th: Если  F в ИП, то ф-ла F≡1 при любой интерпретации, т.е. для
F в ИП, то ф-ла F≡1 при любой интерпретации, т.е. для  м-ва M.; Доказать А1-А3; P1=
м-ва M.; Доказать А1-А3; P1=  xF(x)→F(t); 1)
xF(x)→F(t); 1)  xF(x)=1=>F(x)≡1 x
xF(x)=1=>F(x)≡1 x  M => F(t)=1 в частности
M => F(t)=1 в частности  xF(x)→F(t)=1→1=1; 2)
xF(x)→F(t)=1→1=1; 2)  xF(x)=0; P1=0→F(t)=1 (из-за лжи следует всё, что угодно, за это она верна всегда); P2=F(t)→
xF(x)=0; P1=0→F(t)=1 (из-за лжи следует всё, что угодно, за это она верна всегда); P2=F(t)→  xF(x); 1)
xF(x); 1)  xF(x)=0=> F(x)≡M 0 => F(t)=0 т.к. t
xF(x)=0=> F(x)≡M 0 => F(t)=0 т.к. t  M; P2=0→0=1; 2)
M; P2=0→0=1; 2)  xF(x)=1 тогда акс P2=F(t)→1=F(t)
xF(x)=1 тогда акс P2=F(t)→1=F(t)  1≡1; Правила вывода: I
1≡1; Правила вывода: I  :Let G→F(x)≡1. Требуется доказать, что G→
:Let G→F(x)≡1. Требуется доказать, что G→  xF(x)=1; 1)Пусть G=0, тогда G→
xF(x)=1; 1)Пусть G=0, тогда G→  xF(x)=0→
xF(x)=0→  xF(x)=1; 2)G=1, по условию G→F(x)≡1; 1→F(x)≡1; 0
xF(x)=1; 2)G=1, по условию G→F(x)≡1; 1→F(x)≡1; 0  F(x)≡1=>F(x)≡1 =>
F(x)≡1=>F(x)≡1 =>  xF(x)=1 => G→
xF(x)=1 => G→  xF(x)=1→1=1; I
xF(x)=1→1=1; I  :
:  ; I
; I  :Let F(x)→G≡1. Требуется доказать, что
:Let F(x)→G≡1. Требуется доказать, что  xF(x)→G=1; 1) G=0 F(x)→0≡1
xF(x)→G=1; 1) G=0 F(x)→0≡1  => F(x)≡0 =>
=> F(x)≡0 =>  xF(x)=0 тогда
xF(x)=0 тогда  xF(x)→G=0→0=1; 2) G=1. Тогда
xF(x)→G=0→0=1; 2) G=1. Тогда  xF(x)→C=
xF(x)→C=  ; Доказать MP.;
; Доказать MP.;
1.15. Интерпретация и непротиворечивость. Th о непротиворечивости ИП: Нет такой формулы F, чтобы  . От противного: Если бы
. От противного: Если бы  F
F  => Th об интерпретации =>
=> Th об интерпретации => 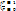
 ; Th о полноте ИП. Если при
; Th о полноте ИП. Если при  интерпретации M F≡1 в интервале M, то
интерпретации M F≡1 в интервале M, то  F в ИП.
F в ИП.
1.16. Метод резолюции в ИП. Эрбранова область. Th дедукции для ИП: Г  А→В => Г,А
А→В => Г,А  В аналогично в ИВ. Th о методе резолюций: F1
В аналогично в ИВ. Th о методе резолюций: F1  F2
F2  …
…  Fn
Fn  ≡0 Это для
≡0 Это для  M => F1,F2,…Fn
M => F1,F2,…Fn  в ИП аналогично в ИВ. Оказывается, достаточно доказать, что G=F1
в ИП аналогично в ИВ. Оказывается, достаточно доказать, что G=F1  F2
F2  …
…  Fn
Fn  ≡0 для множества H – эрбранова обл. H строится так: 1) Правило G к сколемовской форме: G=
≡0 для множества H – эрбранова обл. H строится так: 1) Правило G к сколемовской форме: G=  x1
x1  x2…
x2…  xk P(x1,x2…xk); 2) Если в ф-ле G имеется const Ci то Ci
xk P(x1,x2…xk); 2) Если в ф-ле G имеется const Ci то Ci  H; Если в ф-ле G нет const, то заводим константу С
H; Если в ф-ле G нет const, то заводим константу С  H; Если в ф-ле G учавствует ф-ия f, то для
H; Если в ф-ле G учавствует ф-ия f, то для  h1,…hn
h1,…hn  H => y=f(h1,…hn)
H => y=f(h1,…hn)  H.
H.
1.17. Дать определение исчисления с равенством. Сформулировать и доказать три свойства равенства. Конкретные аксиоматические теории получаются из исчисления предикатов добавлением собственных аксиом, предметных констант, предикатных и функциональных символов. Пример: рассмотрим аксиоматическую теорию с равенством (EQ). К исчислению предикатов добавим конкретный предикат Р(х,у), который обозначим через х=у и две новые аксиомы: Еq1  х (х=х), Еq2 (х=у)
х (х=х), Еq2 (х=у)  (F(х)
(F(х)  F(x//у)), где частичная подстановка F(х//у)) означает правильную замену в формуле некоторых вхождений переменой х на переменную у. Свойство 1. В теории с равенством
F(x//у)), где частичная подстановка F(х//у)) означает правильную замену в формуле некоторых вхождений переменой х на переменную у. Свойство 1. В теории с равенством  t= t, где t – терм. Доказательство состоит из следующих утверждений: ⊢
t= t, где t – терм. Доказательство состоит из следующих утверждений: ⊢  х(х = х) – аксиома Eq1; ⊢
х(х = х) – аксиома Eq1; ⊢  х(х = х)
х(х = х)  (t = t) – аксиома Р1 исчисления предикатов; ⊢ (t = t) – из 1) и 2) по правилу modus ponens. Свойство 2. В теории EQ имеет место симметричность равенства, т.е. х = у ⊢ у = х. Доказательство состоит из следующих утверждений: 1) ⊢(х = у)
(t = t) – аксиома Р1 исчисления предикатов; ⊢ (t = t) – из 1) и 2) по правилу modus ponens. Свойство 2. В теории EQ имеет место симметричность равенства, т.е. х = у ⊢ у = х. Доказательство состоит из следующих утверждений: 1) ⊢(х = у)  ((х = х)
((х = х)  (у = х)) – аксиома Eq2, в которой в качестве F(x) взяли формулу х = х; 2) х = у ⊢ (х = х)
(у = х)) – аксиома Eq2, в которой в качестве F(x) взяли формулу х = х; 2) х = у ⊢ (х = х)  (у = х) – из 1) по теореме деукции; 3) х = у, х = х⊢ у = х – из 2) по тоеореме дедукции; 4) ⊢ х = х – по свойству 1; 5) х = у⊢ у = х – из 3) удалением выводим гипотезы х = х. Свойство 3. В теории EQ имеет место транзитивность равенства, т.е. х = у, у = z ⊢x = z. Доказательство состоит из следующих утверждений: 1) ⊢ (у = х)
(у = х) – из 1) по теореме деукции; 3) х = у, х = х⊢ у = х – из 2) по тоеореме дедукции; 4) ⊢ х = х – по свойству 1; 5) х = у⊢ у = х – из 3) удалением выводим гипотезы х = х. Свойство 3. В теории EQ имеет место транзитивность равенства, т.е. х = у, у = z ⊢x = z. Доказательство состоит из следующих утверждений: 1) ⊢ (у = х)  ((у = z)
((у = z)  (х = z)) – аксиома Еq2, в которой в качестве F(у) взяли формулу у = z; 2) у = х⊢ (у = z) – из 1) по теореме дедукции; 3) х = у ⊢ у = х – по свойству 2; 4) х = у ⊢ (у = z)
(х = z)) – аксиома Еq2, в которой в качестве F(у) взяли формулу у = z; 2) у = х⊢ (у = z) – из 1) по теореме дедукции; 3) х = у ⊢ у = х – по свойству 2; 4) х = у ⊢ (у = z)  (х = z) – из 3) и 2) по транзитивности вывода; 5) х = у, у = z ⊢ х = z – из 4) по теореме дедукции.
(х = z) – из 3) и 2) по транзитивности вывода; 5) х = у, у = z ⊢ х = z – из 4) по теореме дедукции.
Дата добавления: 2015-08-21; просмотров: 84 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Діти в школі | | | Дать определение формальной арифметики. Сформулировать теорему Геделя о неполноте. |