ПРИМЕР 7

Электронная компания определила спрос на ТХ512 полупроводники в объеме 8000 в год. Фирма в течение года работает 200 рабочих дней. В среднем доставка занимает три рабочих дня. Рассчитываем точку перезаказа:

d = (Дневной спрос) = (D / Число рабочих дней) = (8000 / 200) = 40,

ROP = (Точка перезаказа) = dL = (40 ед. / день) 3 дня = 120 ед.

Отсюда, когда хранящийся запас упадет до 120 единиц, должен быть размещен заказ. Заказ прибудет три дня спустя, как раз когда запас истощится.

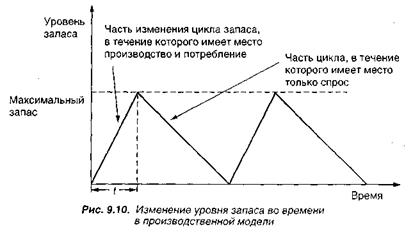
Модель производственного (по количеству) заказа. В пре­дыдущей модели управления запасом мы предполагали, что все количество единиц заказа поступало одновременно. Однако встречаются случаи, когда фирма может пополнять ее запасы в течение определенного периода времени. Такие случаи требуют использования иной модели, которая исключает предположение об одновременности получения заказа. Эта модель используется, когда запасы непрерывно поступают и восстанавливаются через определенное время, т. е. когда изделия производятся и продаются одновременно. В таких условиях мы должны принять во внима­ние дневную производительность (или скорость притока запаса) и скорость дневного расхода запаса. Рис. 9.10 показывает уровень запасов как функцию времени.

Поскольку эта модель, главным образом, подходит для исполь­зования в производственной ситуации, она часто называется мо­делью производственного заказа. Она хорошо себя проявляет, когда запасы наращиваются в течение времени, и традиционный пока­затель экономичного уровня заказа уже предположительно уста­новлен. Мы получим эту модель, полагая затраты на заказ или переналадку, равными затратам на хранение, рассчитанным для Q*. Используя следующие обозначения, мы можем определить выражения для годовых затрат хранения запасов в модели дейст­вующего производства:

Q – количество единиц на заказ;

Н – затраты хранения единицы в год;

р – дневная производительность (скорость производства);

d – ежедневный спрос (скорость потребления);

t – продолжительность производственного процесса в днях.

1. (Годовые затраты хранения запаса) =

= (Средний уровень запаса) (Затраты хранения единицы в год) =

= (Средний уровень запаса) Н.

2. (Средний уровень запаса) =

= (Максимальный уровень запаса) / 2.

3. (Максимальный уровень запаса) =

= (Общий результат производства за период производства) –

– (Общий результат потребления за период производства) = pt – dt.

Но Q – общий результат производства = pt и t = Q/p. Поэтому максимальный уровень запаса = р (Q / p) – d (Q / p) = Q – (d / p) Q = Q(1 – d / p).

4. (Годовые затраты хранения запаса или просто затраты хране­ния) =

= (Максимальный уровень запаса) (Н) / 2 = QH (1 – d / p) / 2.

Используя выражение для затрат хранения и выражения для затрат переналадки, полученные на основе EOQ – модели, мы по­лучим систему уравнений для определения оптимального числа единиц на заказ:

(Затраты переналадки) = (D/Q)S;

(Затраты хранения) = HQ (1 – d/p)/2.

Чтобы определить Q*, необходимо приравнять затраты заказа к затратам хранения по определению, данному выше.

DS/Q = HQ (1 – d/p)/2, Q^2 = 2DS/(H (1 – d/p)), Q* = sqr (2DS/(H(1 – d/p))).

(9.7)

Мы можем использовать полученное выражение, чтобы опре­делить оптимальный заказ или производственный задел, кото­рый расходуется одновременно в процессе производства и потреб­ления.

Дата добавления: 2015-08-21