Основные обозначения, расчетные формулы и определения

Индуктивные катушки называются связанными, если изменение тока в одной вызывает появление ЭДС в остальных. Наблюдаемое явление называется взаимоиндукцией, а наведенная ЭДС – ЭДС взаимоиндукции.

Магнитный поток, пронизывающий катушку и вызванный протекающим по ней током, носит название магнитного потока самоиндукции (Ф₁₁). Его можно представить в виде двух составляющих: первая пронизывает витки связанной с первой второй катушки и называется потоком взаимоиндукции (Ф₂₁), вторая -магнитный поток рассеяния первой катушки (Ф_S1) – не пронизывает витки второй катушки. Таким образом, Ф₁₁ = Ф₂₁ + Ф_S1. Аналогичные соотношения справедливы и для магнитного потока второй катушки. При этом полный магнитный поток, пронизывающий первую катушку, изменяется на величину, обусловленную влиянием второй: Ф₁ = Ф₁₁ ± Ф₁₂. Знак плюс здесь соответствует совпадающим по направлению магнитным потокам самоиндукции и взаимоиндукции (согласное включение), а минус – противоположным (встречное включение).

Потокосцепление и ЭДС, наводимая в первой катушке индуктивности, также имеют две составляющие

, . (3.1)

Преобразуя выражение для и введя понятия индуктивности катушки и взаимной индуктивности двух катушек , напряжение на первой катушке запишем в виде

. (3.2)

При гармоническом внешнем воздействии это напряжение можно представить в виде

. (3.3)

Количественно степень связи между катушками характеризует коэффициент индуктивной связи :

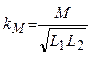. (3.4)

Одним из наиболее важных применений явления взаимоиндукции является использование его в трансформаторах – устройствах для передачи энергии из одной части электрической цепи в другую. При этом, обмотка, подключенная к источнику энергии, носит название первичной, а обмотки подключенные к нагрузке называются вторичными. Трансформатор с ферромагнитным сердечником является нелинейным устройством (процессы в нем описываются нелинейными дифференциальными уравнениями), трансформатор без сердечника (исследуется в лабораторной работе) – линейный (рис. 3.1).

Основной задачей, которая решается при анализе трансформатора, является установление связи между напряжениями и токами на его зажимах.

Рис. 3.1 Эквивалентная схема трансформатора

Наиболее простые соотношения при этом получаются для совершенного трансформатора – трансформатора у которого отсутствуют потери: R_L1 = R_L2 = 0 и коэффициент индуктивной связи между обмотками . Если же в совершенном трансформаторе ток намагничивания , то получаем идеальный трансформатор, в котором

,

. (3.5)

Здесь - коэффициент трансформации.

Из выражений (3.5) следует, что мощности, потребляемые идеальным трансформатором, равны мощностям, отдаваемым им в нагрузку P₁ = P₂. Из выражений (3.5) следует также то, что входное сопротивление нагруженного трансформатора

. (3.6)

Свойство трансформатора преобразовывать модуль сопротивления используется для согласования сопротивлений источника и нагрузки.

Дата добавления: 2015-08-21