Постановка задачи. Для разработки общей методики решения краевых задач в среде программы MS Excel

Для разработки общей методики решения краевых задач в среде программы MS Excel рассматривается решение конкретного случая краевой задачи, определяемой уравнением (1), и коэффициентами

(13)

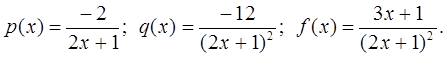
при граничных условиях

(14)

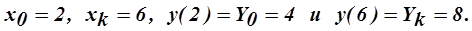
Запишем рассматриваемый пример при n равном 5. Таким образом, число узлов сетки равно 6, а формат системы соответствует (11).

Решение системы (12) ищется в виде

(15)

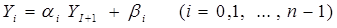
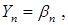
где a_i, β_i - неизвестные прогоночные коэффициенты [4].

Значения коэффициентов a_i и β_i, как показано в [ 4 ], вычисляются по формулам прямого хода метода прогонки. Запишем уравнение (15) для i = 0:

(16)

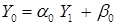
Приведём первое уравнение системы (12)

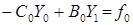
к виду (16). Для этого перенесем член B₀Y₁ в правую часть и разделим уравнение на –С ₀ .

(17)

Сравнивая (16) и (17) получаем значения прогоночных коэффициентов α₀ и β₀.

(18)

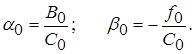
Рассматривая остальные уравнения системы (12) получим общие рекуррентные формулы для коэффициентов α_i и β_i.

(19)

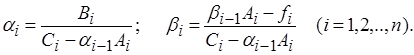
Запишем систему уравнений, состоящую из уравнения (16) для i = n-1 и последнего уравнения системы (12):

(20)

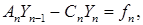
Решая систему (20) и используя формулу (15) при i = n, находим выражение для Y _n и соответствующий ему коэффициент прогонки β_n :

(21)

(22)

Определив значение β_n, по формулам (15) находим в обратном порядке решение системы (12):

.

Как уже отмечено выше, в рассматриваемом нами случае системы (11), если следовать традиционной записи, использованной в (12), значение А₀ = 0, С₀ =-1, а значение В₀ =0. Аналогично для последнего уравнения имеем значение А_n = 0 и С_n =-1, В_n =0.

Рассмотрим последовательность шагов решения на примере уравнения (1) с учетом (13), (14), приведенных выше.

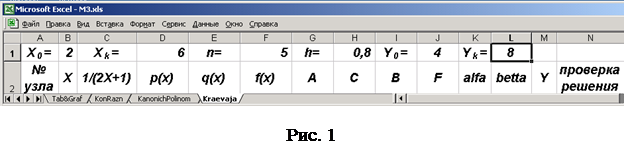
Для того чтобы обеспечить в дальнейшем наглядность и понятность вычислений, заполним таблицу значениями функций p(x), q(x) и f(x), вычисленными в узловых точках при n=5. Для определения значения h выполним на листе Excel следующие операции (рис.1):

▬ в ячейки А1, С1, Е1 и G1 введём комментарии: 'Х₀=', 'Х_k=', 'n=' и 'h=',

▬ в ячейку В1 введем значение аргумента Х₀ равное 2,

▬ в ячейку D1 введем значение аргумента Х_k равное 6,

▬ в ячейку F1 введем значение аргумента n равное 5,

▬ в ячейку H1 введем формулу "=(D1-B1)/F1" [1], определяющую значение шага между узлами формируемой сетки как

.

	Рис. 1

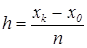▬ В ячейках второй строки таблицы оформим заголовок таблицы так, как это показано на рис. 1.

Определив основные параметры таблицы, заполним столбцы значениями в соответствии с заголовком таблицы, показанным на рис. 1. Для этого выполним следующие действия:

1. В ячейки А3:А8 введём индексы строк. Для этого в ячейку А3 введём цифру 0 – индекс первого узла. Переводим УМ [2]⁾ в правый нижний угол ячейки А3, ФЛКМ и, зафиксировав клавишу Ctrl, протянем УМ от ячейки А3 до ячейки А8.

2. В ячейку B3 вводим ссылку на ячейку с начальным значением аргумента Х₀: "=В1". Значение ссылки формируется, если подвести УМ к ячейке, накоторую делается ссылка и сделать ЩЛК.

3. Заполняем ячейки столбца В, выполняя вычисление значений аргумента х в соответствии с формулой

Для этого в ячейку B4 вводим формулу "=В3+$H$1", которую протягиваем до ячейки B8, в которой достигается значение равное значению x_n = Х_k. (Для формирования абсолютной ссылки на ячейку Н1 после ЩЛК по ячейке Н1 следует нажать функциональную клавишу F4).

4. В ячейках от C3 до C8 вычисляем значения вспомогательной функции 1/(2 х_i + 1), входящей взнаменатели функций p(x), q(x) и f(x). Вводим в C3 формулу "=1/(2*B3+1)" и протягиваем эту формулу до ячейки C8;

5.

В ячейки D3, E3 и F3 записываем формулы, соответствующие (13), для вычисления значений функций p(x), q(x) и f(x). Запись этих формул при вводе их в ячейки таблицы имеет следующий вид: "=-2*C3", "= ‑12*C3*C3" и "=(3*B3+1)*C3*C3" соответственно. При протягивании этих формул по столбцам D, Е и F до восьмой строки таблица заполняется так, как показано на рис. 2.

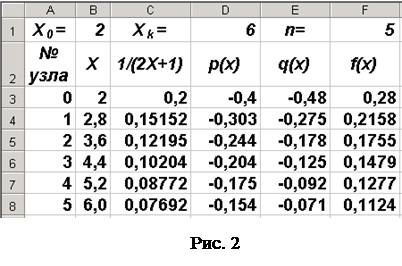6. Далее начинаем заполнение столбцов G, H, I и J значениями коэффициентов A_i, C_i, B_i и F_i в соответствии с форматом системы уравнений (11). В ячейки G3, H3, I3 записываем значения, определяемые форматом первого уравнения системы (11): A₀=0, C₀=-1, В₀=0. В ячейку J3 записываем ссылку на ячейку J1, в которой записано начальное значение F₀=Y₀: "=J1".

7. В ячейки G8, H8, I8 записываем значения, определяемые конечными условиями A₅=0, C₅=-1, В₅=0. В ячейку J8 записываем ссылку на ячейку L1, в которой записано начальное значение F_k= F₅ = Y_k:"=L1".

8.

Далее заполняем столбцы G, H, I и J значениями коэффициентов A_i, C_i, B_i и F_i. В ячейку G4 вводим формулу "=1-D4*$H$1/2", соответствующую формуле

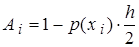для вычисления коэффициента A₁. После чего протягиваем эту формулу до ячейки G7.

9.

Аналогично в ячейку Н4 вводим формулу для вычисления коэффициента С₁: "2-Е4*$H$1*$H$1", а в ячейку I4 вводим формулу для вычисления коэффициента B₁: "1+D4*$H$1/2", реализуя соответствующие формулы

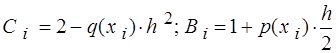Протягиваем эти формулы до ячеек Н7 и I7.

10.
В ячейках столбца J формируем вектор правых частей системы уравнений (11). В ячейку J4 вводим формулу “=F4*$H$1*$H$1”, соответствующую формуле F_i = f_ih². Протягиваем эту формулу до ячейки J7. В результате получаем таблицу, показанную на рис. 3. Следует отметить, что в столбцах G, H, I и J этой таблицы записаны элементы матрицы, решаемой системы уравнений (11).

Рис. 3

11. Используя вычисленные значения коэффициентов A_i, C_i, B_i и F_i, находим в соответствии с формулами (18) и (19) значения коэффициентов a_i и b_i. В ячейку K3 запишем формулу для вычисления a ₀: "=I3/H3", а в ячейку L3 формулу для вычисления b₀.: "=-J3/H3". И далее в ячейки K4 и L4 вводим формулы, соответствующие (19), для вычисления коэффициентов

a ₁ :"=I4/(H4-K3*G4)", и b₁: "=(G4*L3‑J4)/(H4‑K3*G4)".

Протягиваем эти формулы до ячеек K8 и L8 соответственно. Результаты вычисления показаны на рис. 4.

12.
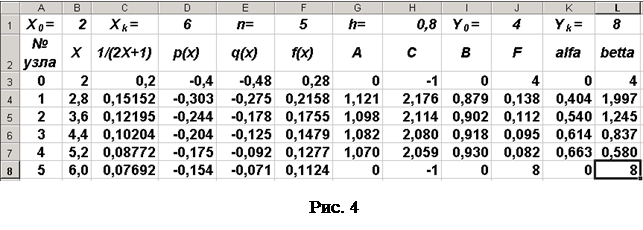
Дальнейшие вычисления выполняются в столбце М по формулам обратного хода (21) и (22). В ячейку М8 введем формулу "=L8", представляющую ссылку на значение b _n. В ячейку М7 введем формулу "=L7+K7*M8", соответствующую и протянем ее до ячейки М3. Результаты вычислений показаны на рис. 5.

13. Построим график функции Y(X), используя возможности мастера диаграмм программы MS Excel. Для этого выделим ячейки столбца значений функции Y(X) от ячейки М3 до М8 ивыполним процедуру создания диаграммы, используя средства "мастера диаграмм" программы MS Excel. Окончательный результат показан на рис. 5.

Дата добавления: 2015-08-21