Применение метода прогонки для решения систем линейных алгебраических уравнений с трёхдиагональными ленточными матрицами

Решение краевой задачи методом конечных разностей

Методические указания по выполнению лабораторной работы в курсе “Информатика” для студентов очной и заочной форм обучения всех специальностей

Санкт-Петербург

УДК 681.3

Решение краевой задачи методом конечных разностей: Методические указания по выполнению лабораторной работы в курсе “Информатика” для студентов очной и заочной форм обучения всех специальностей/ СПбГАСУ; Сост.: Любимов Е.Б., Любимов Б.Е., Мовсесова Л. В. СПб., 2005. 16 c.

В этой работе рассматриваются основные вопросы и примеры решения задач, приводящихся к формату краевой задачи и рассматриваемых при изучении раздела "Вычислительная математика" в курсе "Информатика". Пособие предназначено для студентов всех специальностей дневной и заочной форм обучения.

Табл. 4. Ил. 5. Библиогр. 4 назв.

Рецензент д-р физ.-мат. наук, профессор Б. Г. Вагер (СПбГАСУ)

Решение краевой задачи методом конечных разностей

Составители: Любимов Евгений Борисович,

Любимов Борис Евгеньевич,

Мовсесова Лия Витальевна

Редактор

Корректор

Компьютерная верстка И.А. Яблоковой

Решение краевой задачи методом конечных разностей

Основные понятия, используемые в постановках краевых задач

В практике строительных расчетов многие математические модели, используемые для расчета конструкций, приводятся к линейным дифференциальным уравнениям второго порядка, имеющим следующий вид:

(1)

,

где x - параметр, определяющий некоторую координату исследуемого объекта, p(x), q(x), f(x) – заданные функции.

К примерам задач, приводящих к уравнениям вида (1), можно отнести задачи расчетов различных балочных конструкций.

Для решения задачи, определяемой (1), необходимо задать дополнительные условия, определяющие состояние исследуемого объекта при некоторых заданных значениях координатной переменной x. Условия, определяющие состояние объекта в заданных точках x, называются граничными [1, 2, 4].

Таким образом, для нахождения решения уравнения (1) необходимо определить граничные условия. Например, следующим образом:

(2)

где Y₀, Y_k –фиксированные числовые значения Y₀ и Y_k, определяющие значения исследуемой координаты.

На конкретном примере рассмотрим алгоритм решения стационарной краевой задачи для объектов, определяемых математическими моделями представленными линейными дифференциальными уравнениями второго порядка вида (1), (2).

Одним из численных методов, применяемых для решения таких уравнений, является метод конечных разностей, называемый также методом сеток. Основой этого метода является замена непрерывной области пространства изменения аргумента х на дискретное множество – "сетку" точек х_i, в которых определяются значения функции y(x_i ) [4].

При использовании метода конечных разностей решение задачи осуществляется в результате последовательной реализации четырех этапов:

1) дискретизация области изменения аргумента х;

2) переход от непрерывной дифференциальной математической модели к конечно-разностной модели исследуемого объекта;

3) оформление разностного аналога краевых условий задачи;

4) решение полученной в результате выполнения первых трех шагов математической системы линейных алгебраических уравнений.

Рассмотрим последовательно выполнение этих этапов для разработки алгоритма решения конкретной краевой задачи.

Во-первых, для дискретизации области изменения аргумента х интервал изменения х разделим на n равных частей. При этом формируется сетка с (n+1) равноотстоящими узлами. Расстояние между узлами (шаг сетки) равен
h = (x_k ‑ x₀ )/n, а значения х_i вузлах сетки легко вычисляются по формуле х_i = х₀ + i · h (i=0,1,2,...,n).

Второй этап перехода от непрерывного дифференциального уравнения (1) к конечно-разностной модели реализуется на базе классического определения производной как предела:

(3)

,

Из (3), получим выражения для аппроксимации первой производной y_i', учитывающие значения функции в двух симметричных относительно х_i узлах:

(4)

)

.

Для вывода разностной формулы второй производной воспользуемся тем, что y'' = (y')', а в записи первой производной используем оба варианта представления производной в формулах (4).

(5)

Подставив выражения (4) и (5) в формулу (1), получим:

Очевидно, что формула (6) будет верна только для внутренних узлов х_i (i=1,2,…,n-1). Умножим (6) на h² и приведем подобные члены. В итоге получим

(7)

Введем дополнительные обозначения:

(8)

,

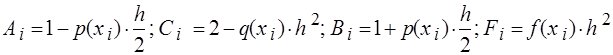и запишем (7), используя обозначения (8). Отметим, что при этом необходимо изменить знак перед коэффициентом C _i.

(9)

Таким образом, мы получили систему уравнений (9), содержащую (n-1) линейное алгебраическое уравнение относительно (n+1) неизвестных y _i (i =0, 1, 2, …,n).

(10)

Окончательное оформление системы уравнений выполняется при записи разностного аналога краевых условий задачи. Недостающие уравнения мы получаем из краевых условий:

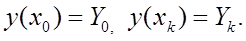Запишем эту систему для случая n = 5.

(11)

Полученная система линейных алгебраических уравнений имеет трехдиагональную матрицу. В первом уравнении этой системы коэффициенты А₀ = 0, С₀ = -1, а В₀ = 0. В пятом уравнении А₅ = 0, С₅ = -1, а В₅ = 0.Одним из эффективных методов решения систем уравнений такого типа является метод прогонки.

Применение метода прогонки для решения систем линейных алгебраических уравнений с трёхдиагональными ленточными матрицами

Полученная нами система уравнений ( 11 ) является частным случаем систем уравнений с трехдиагональными ленточными матрицами.Ниже приведена общая форма записи таких систем:

Дата добавления: 2015-08-21