Проверка правильности полученного решения

Для проверки правильности полученного в столбце М решения Y(X) выполняется подстановкой полученного решения в уравнения исходной системы. В ячейки столбца N последовательно вводим формулы, реализующие вычислительный алгоритм, определяемый системой уравнений (11). В N3 введём формулу "=M3". Затемв N4 введём формулу "=G4*M3‑H4*M4+I4*M5", реализующую левую часть уравнения (9). Эту формулу протягиваем до N8, получаясоответственно – "=G5*M4‑H5*M5+I5*M6" в N5, "=G6*M5-H6*M6+I6*M7" в N6, "=G7*M6‑H7*M7+I7*M8" в N7 и "=G8*M7-H8*M8+I8*M9" в N8. Полученные в столбце N значения совпадают со значениями в столбце J, что позволяет судить о правильности полученного решения.

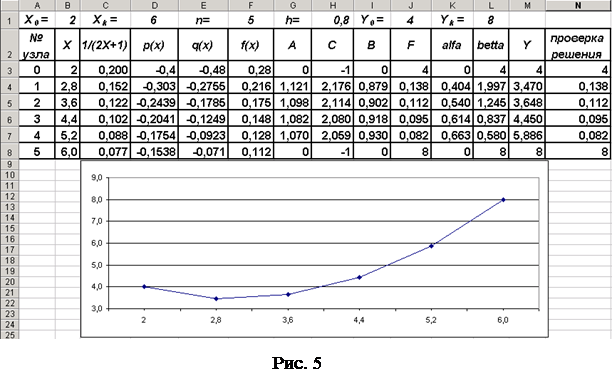Варианты заданий для выполнения самостоятельной работы

Методом конечных разностей найти решение краевой задачи на сетке из 6 узлов.

Вариант 1

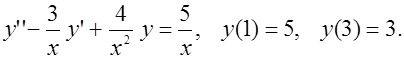
Вариант 2

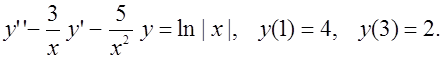
Вариант 3

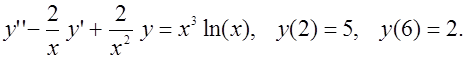
Вариант 4

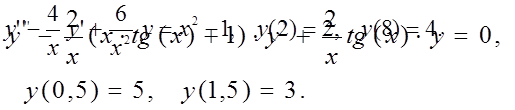
Вариант 5

Вариант 6

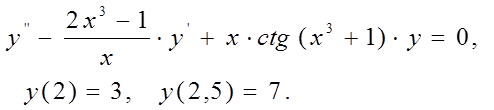
Вариант 7

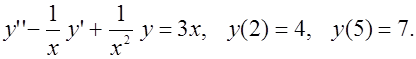
Вариант 8

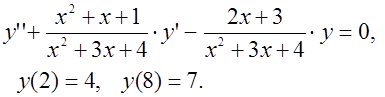
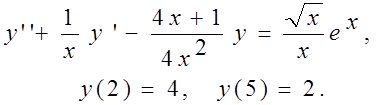
Вариант 9

Вариант 10

Вариант 11

Вариант 12

Вариант 13

Вариант 14

Вариант 15

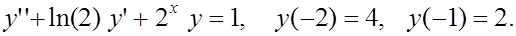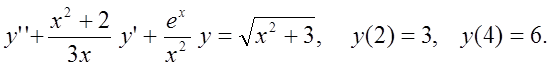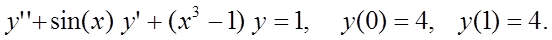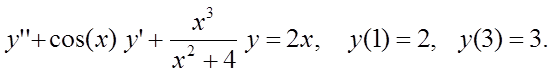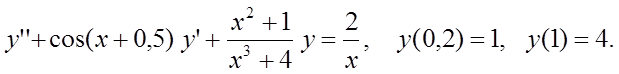Литература

1. Пискунов Н.С. Дифференциальное и интегральное исчисления. М.:Физматгиз, 1963. – 856 с.

2. Карпов В.В., Коробейников А.В. Математические модели задач строительного профиля и численные методы их исследования: Учеб. пособие. – СПб., СПбГАСУ, 1996. – 134 с.

3. Бахвалов Н.С. Численные методы. – М.:Наука, 1973. – 632 с.

4. Вагер Б.Г. Численные методы решения дифференциальных уравнений: Учеб. пособие – СПбГАСУ. – СПб. 2003. 114 с.

5. Любимов Е.Б. и др. Решение систем линейных алгебраических уравнений средствами программы Microsoft Excel: Метод. указ. – СПб., СПбГАСУ, 2005. – 22 c.

СОДЕРЖАНИЕ

Основные понятия, используемые в постановках краевых задач. 3

Применение метода прогонки для решения систем линейных алгебраических уравнений с трёхдиагональными ленточными матрицами. 6

Реализация метода прогонки в среде программы MS Excel 6

Постановка задачи. 6

Проверка правильности полученного решения. 12

Варианты заданий для выполнения самостоятельной работы.. 13

Литература. 16

[1]) Формулы вводятся в ячейки таблиц, начиная с символа “=” (равно). Двойные кавычки использованы в тексте для выделения формулы. Вводить их в ячейки таблицы не нужно.

[2]) Терминология и сокращения, используемые в тексте методических указаний, приведены в начальном разделе методических указаний к первой лабораторной работе:[5].

Дата добавления: 2015-08-21