Факторы, определяющие направление протекания химиче­ских реакций.

В предыдущих параграфах мы рассмотрели не­сколько примеров, показывающих, что при определенных условиях каждая химическая реакция самопроизвольно протекает в опреде­ленном направлении. Так, при низких температурах экзотермиче­ская реакция образования парообразной воды

2Н₂ + О₂ = 2Н₂О+ 483,6 кДж

практически нацело протекает в прямом направлении. В отсутствие катализатора скорость этой реакции при обычных условиях крайне мала. Однако, при наличии катализатора (например, платинированного асбеста) процесс образования воды протекает с большой скоростью.

Но при высоких температурах эта реакция начинает идти в обратном на­правлении: водяной пар разлагается на водород и кислород. Во всех случаях в результате реакции может быть достигнуто состоя­ние устойчивого химического равновесия, но само положение рав­новесия при разных условиях оказывается различным.

Возникает вопрос: в чем причина определенной направленности химических процессов, какие факторы обусловливают то или иное состояние химического равновесия?

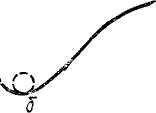
Известно, что в механических системах устойчивое равновесие соответствует минимуму потенциальной энергии системы. Так, ша­рик самопроизвольно скатывается из положения а на наклонной поверхности (рис. 69), причем его потенциальная энергия перехо­дит сначала в кинетическую энергию движения шарика как целого, а затем в энергию теплового движения молекул. В положении б шарик находится в равновесии.

Естественно предположить, что и химические процессы должны самопроизвольно протекать в направлении уменьшения внутрен­ней энергии системы, т. е. в направлении, отвечающем положи­тельному тепловому эффекту реакции. Действительно, опыт пока­зывает, что при обычных условиях самопроизвольно протекают преимущественно экзотермические реакции.

Однако попытка объяснить направленность химических процес­сов только стремлением к минимуму внутренней энергии приводит к противоречиям с фактами. Так, уже при обычных температурах самопроизвольно протекают эндотермические процессы растворе­ния многих солей и некоторые эндотермические химические реак­ции.

Рис. 69. Шарик самопроизвольно скатывается из положения а в положение б.

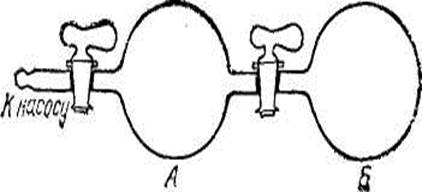
Рис. 70. Сосуд, состоящий из дзух частей: в части А находится разреженный газ, в части Б — вакуум.    

С повышением температуры все большее число реакций начи­нает самопроизвольно протекать в направлении эндотермического процесса; примерами таких реакций могут служить упомянутое выше разложение воды или протекающий при высоких температу­рах синтез оксида азота(II):

0,5 N₂ + 0,5 O₂ = NO - 90,4 кДж

Более того, принцип стремления к минимуму внутренней энер­гии требует, чтобы все экзотермические реакции доходили до конца, т. е. исключает возможность обратимых реакций; однако та­кие реакции реально существуют.

Вспомним теперь, что среди механических систем имеются та­кие, поведение которых тоже нельзя описать только направлен­ностью процессов к достижению минимума потенциальной энергии. Это системы, состоящие из очень большого числа частиц. Напри­мер, молекулы, входящие в состав воздуха, распределяются вокруг Земли в виде атмосферы многокилометровой толщины, но не па­дают на Землю, хотя минимуму потенциальной энергии каждой молекулы соответствует наиболее низкое ее положение.

Из громадного числа частиц состоят и химические системы. Поэтому неудивительно, что и здесь тенденция к достижению ми­нимума внутренней энергии не является единственным фактором, определяющим их поведение.

Для того чтобы составить представление о втором факторе, влияющем на направление реакций, рассмотрим какой-либо само­произвольно протекающий процесс, не сопровождающийся тепло­вым эффектом. Примером такого процесса может служить расши­рение разреженного газа.

Пусть в части А сосуда, разделенного на две части (рис. 70), находится разреженный газ. В таком газе среднее расстояние между молекулами велико; при этом условии внутренняя энергия газа не зависит от степени его разрежения. Вторая половина со­суда (Б) газа не содержит. Если открыть кран, соединяющий обе части сосуда, то газ самопроизвольно распространится по всему сосуду. Внутренняя энергия газа при этом не изменится; тем не менее, самопроизвольно произойдет именно процесс расширения газа, а обратный процесс — самопроизвольное сжатие газа — не происходит.

Причины такой направленности процесса можно понять, если сначала рассмотреть систему, содержащую небольшое число моле­кул. Пусть в сосуде находятся всего две молекулы, которые обо­значим 1 и 2. Равномерное распределение газа между обеими частями сосуда, соответствующее определенному макросостоянию газа (Макросостояние — состояние вещества, характеризующееся опреде­ленными значениями его макроскопических свойств (температура, давление, объем и т. д.); микросостояние — состояние вещества, характеризующееся определенным состоянием каждой частицы (молекулы, атомы). Одно и то же макросостояние соответствует большому числу различных микросостояний) может осуществиться двумя м икросостояниями:

А	Б

Макросостояние, при котором весь газ сосредоточен в одной из частей сосуда (например, в части А), осуществляется единствен­ным микросостоянием:

А	Б
1,2	-

Очевидно, что то или иное макросостояние системы тем более вероятно,

чем большим числом микросостояний оно может осу­ществиться.

В рассматриваемом случае (две молекулы) равномер­ное распределение

газа по сосуду вдвое вероятнее, чем переход всего газа в часть сосуда А.

Пусть теперь в сосуде находится четыре молекулы, которые мы вновь

пронумеруем. Переходу всего газа в часть сосуда А по-прежнему

соответствует единственное микросостояние:

А	Б
1,2,3,4	-

Между тем, равномерное распределение газа между обеими частями сосуда может теперь осуществляться шестью различными микросостояниями:

А	Б	А	Б	А	Б
1,2   1,3	3,4 2,4	1,4 2,3	2,3 1,4	2,4 3,4	1,3 1,2

Теперь, следовательно, вероятность равномерного распределения молекул газа по всему объему сосуда оказывается заметно более высокой, чем вероятность их перехода в одну из его частей. Естественно, что равномерное распределение газа будет наблю­даться гораздо чаще, чем полное его сосредоточение в части сосуда.

Если в сосуде находится шесть молекул, то переходу нх в одну из частей сосуда (т. е. самопроизвольному сжатию газа до половины занимаемого им первоначального объема), как и раньше, соответствует только одно микросо­стояние. Но равномерному распределению газа между обеими частями сосуда отвечает уже 20 возможных комбинаций молекул, т. е. 20 различных микро­состояний:

А	Б	Л	Б	А	Б	А	Б
1,2,3	4,5,6	1,3,5	2,4,6	2,3,4	1,5,6	2,5,6	1,3,4
1,2,4	3,5,6	1,3,6	2,4,5	2,3,5	1,4,6	3,4,5	1,2,6
1,2,5	3,4,6	1,4,5	2,3,6	2,3,6	1,4,5	3,4,6	1,2,5
1,2,6	3,4,5	1,4,6	2,3,5	2,4,5	1,3,6	3,5,6	1,2,4
1,3,4	2,5,6	1,5,6	2,3,4	2,4,6	1,3,5	4,5,6	1,2,3

Теперь явление самопроизвольного сжатия газа, т е. сосредоточения всех его молекул в одной из частей сосуда, будет наблюдаться еще реже; равномер­ное же распределение газа по всему сосуду становится еще более вероятным.

Таким образом, с ростом числа молекул вероятность беспоря­дочного, равномерного распределения газа в сосуде очень быстро возрастает, а самопроизвольное сжатие газа становится все менее вероятным процессом. Если мы вспомним теперь, что макроскопи­ческие количества газа содержат огромное число молекул, то ста­нет ясно, что в реальном опыте самопроизвольное сжатие газа представляет собой процесс практически невозможный, и что само­произвольно будет протекать обратный процесс расширения газа, приводящий к равномерному, беспорядочному распределению его молекул по всему объему сосуда.

Рассмотренное нами явление расширения газа представляет собой пример проявления принципа направленности процессов к наиболее вероятному состоянию, т. е. к состоянию, которому со­ответствует максимальная беспорядочность распределения частиц. Направление самопроизвольного протекания химических реакций и определяется совокупным действием двух факторов: тенденцией к переходу системы в состояние с наименьшей внутренней энергией и тенденцией к достижению наиболее вероятного состояния.

Так, в приведенном примере с воздухом тенденция к минимуму потенциальной энергии заставляет молекулы, входящие в состав воздуха, падать на Землю, а тенденция к максимальной вероятно­сти заставляет их беспорядочно распределяться в пространстве. В результате создается некоторое равновесное распределение молекул, характеризующееся более высокой их концентрацией у поверхности Земли и все большим разрежением по мере удале­ния от Земли.

В системах соль — вода минимум внутренней энергии в боль­шинстве случаев соответствует кристаллическому состоянию соли. Однако наиболее вероятное состояние системы достигается при беспорядочном распределении соли в жидкой воде. В результате совместного действия этих двух факторов устанавливается равно­весие, соответствующее определенной концентрации насыщенного раствора соли.

При химических реакциях в силу принципа направленности процессов к минимуму внутренней энергии атомы соединяются в такие молекулы, при образовании которых выделяется наиболь­шее количество энергии. В силу же принципа направленности про­цессов к наиболее вероятному состоянию протекают такие реак­ции, в ходе которых возрастает число частиц (например, реакции разложения молекул на атомы) или чисто возможных состояний атомов.

Так, в случае реакции

N₂ + 3H₂ = 2NH₃+ 92,4 кДж

минимальной внутренней энергии системы соответствует аммиак, образующийся при протекании реакции до конца вправо. Однако наиболее вероятному состоянию системы отвечает азото-водород-ная смесь, образующаяся при полном разложении аммиака, ибо при этом в 2 раза возрастает число молекул газов. Вследствие действия обоих фактором в системе устанавливается равновесие, отвечающее определенному при данной температуре соотношению концентраций всех веществ. В случае реакции

N₂ + O₂ = 2NO - 180,8 кДж

минимальной внутренней энергии отвечает азото-кислородиая смесь, образующаяся при полном разложении оксида азота. По­скольку в ходе этой реакции число частиц не изменяется, то про­текание реакции до конца как в прямом, так и в обратном на­правлении не увеличивает вероятности состояния системы. Не изменяется при этом и число возможных состояний атомов: в ис­ходных веществах каждый атом и азота, и кислорода связан с атомом того же элемента (молекулы N₂ и О₂), а в продукте реак­ции каждый атом связан с атомом другого элемента (молекула N0). Иначе обстоит дело при частичном протекании процесса в прямом или в обратном направлении. В результате частичного прохождения реакции, т. е. при сосуществовании исходных веществ и продуктов реакции, атомы азота и кислорода находятся в двух состояниях: часть их связана в молекулы N₂ и О₂, а часть — в молекулы N0, Таким образом, число возможных микросостояний рассматриваемой системы, а следовательно, и вероятность соот­ветствующего ее макросостояния возрастают при частичном про­текании реакции. Итак, тенденция к уменьшению внутренней энергии способствует протеканию данной реакции до конца в обратном направлении, а тенденция к увеличению вероятности со­стояния вызывает ее частичное протекание в прямом направлении. Вследствие одновременного действия обоих факторов часть азото-кислородной смеси при нагревании превращается в N0 и устанав­ливается равновесие между исходными веществами и продуктом реакции.

Тенденция к переходу в состояние с наименьшей внутренней энергией проявляется при всех температурах в одинаковой сте­пени. Тенденция же к достижению наиболее вероятного состояния проявляется тем сильнее, чем выше температура. Поэтому при низких температурах в большинстве случаев практически сказы­вается только влияние первой из этих тенденций, в результате чего самопроизвольно протекают экзотермические процессы. По мере возрастания температуры равновесие в химических системах все больше и больше сдвигается в сторону реакций разложения или увеличения числа состояний атомов. При этом каждой температуре отвечает состояние равновесия, характеризующееся определенным соотношением концентраций реагирующих веществ и продуктов реакции.

Оба рассмотренных фактора, а также результат их совместного действия можно выразить количественно. Величины, с помощью которых это делается, изучаются в разделе физики — термоди­намике и называются термодинамическими величи­нами. К ним относятся, в частности, внутренняя энергия, энталь­пия, энтропия и энергия Гиббса.

Термодинамические величины. Внутренняя энергия и энталь­пия.

Внутренняя энергия U вещества (или системы) — это полная энергия частиц, составляющих данное вещество. Она слагается из кинетической и потенциальной энергий частиц. Кинетическая энергия — это энергия поступательного, ко­лебательного и вращательного движения частиц; потенциальная энергия обусловлена силами притяжения и отталкивания, дей­ствующими между частицами.

Внутренняя энергия зависит от состояния вещества. Изменение внутренней энергии системы Δ U при том или ином процессе можно определять. Пусть в результате какого-нибудь процесса система переходит из начального состояния 1 в конечное состояние 2, со­вершая при этом работу А и поглощая из внешней среды тепло­ту Q. В термохимических уравнениях положительной принято счи­тать теплоту, выделенную системой. В уравнениях термодинамики принято обратное условие: положительной считается теплота, поглощенная системой.

Внутренняя энергия системы уменьшится на величину А, возрастет на величину Q и в конечном состоянии бу­дет равна

U₂=U_l + Q - А

где U₁ и U₂— внутренняя энергия системы в начальном (1) и в ко­нечном (2) состояниях. Если обозначить разность U₂ — U₁через Δ U, то уравнение можно представить в виде:

Δ U = Q - A

Это уравнение выражает закон сохранения энергии, согласно которому изменение внутренней энергии не зависит от способа проведения процесса, а определяется только начальным и конечным состояниями системы. Однако какая часть энергии пой­дет на совершение работы, а какая превратится в теплоту — зави­сит от способа проведения процесса: соотношение между работой и теплотой может быть различным.

В частности, если в ходе про­цесса не производится никакой работы, в том числе работы рас­ширения против внешнего давления, т. е., если объем системы не изменяется, то

Δ U = Q_v

где Q_v — теплота, поглощенная системой в условиях постоянного объема.

Последнее уравнение дает возможность определять изменение внутренней энергии при различных процессах. Например, в случае нагревания вещества при постоянном объеме изменение внутрен­ней энергии определяется по теплоемкости этого вещества:

Δ U = Q_v = nCv ΔT

Здесь C_v — молярная теплоемкость вещества при постоянном объеме; п — количество вещества; ΔT —разность между конечной и начальной температурами.

В случае химической реакции, протекающей без изменения объема системы, изменение внутренней энергии равно взятому с обратным знаком тепловому эффекту этой реакции.

Энтальпия.

Однако чаще в химии приходится иметь дело с процессами, протекающими при постоянном давлении. При этом удобно пользоваться величиной энтальпии Н, определяемой соотношением:

Н = U + PV

При постоянном давлении и при условии, что в ходе процесса совершается только работа расширения (А = PΔV). Работа (А)против силы внешнего давления равна

величине этой силы (F), умноженной на путь (Δ l), т. е. А = F Δl. Но сила равна давлению (P), (умноженному на ту площадь (S), на которую оно действует: F = PS, откуда А = PS Δ l или А = PΔV)

ΔН = ΔU + P ΔVили

ΔU = ΔН — Р ΔV

Сравнивая последнее уравнение с уравнением внутренней энер­гии

Δ U = Q - A

видим, что при указанных условиях ΔН = Q_р, где где Q_р— теплота, поглощенная системой при постоянном дав­лении.

Последнее уравнение дает возможность определять изменение энтальпии при различных процессах. Такие определения анало­гичны определениям внутренней энергии, с той разницей, что все измерения должны проводиться в условиях постоянного давления. Так, при нагревании вещества изменение его энтальпии опреде­ляется по теплоемкости этого вещества при постоянном давлении

ΔН = Q_P = пС_р ΔT

где п — количество вещества; С_р — молярная теплоемкость веще­ства при постоянном давлении.

При изменениях агрегатного состояния вещества и при алло­тропных переходах изменение энтальпии равно по величине, но обратно по знаку теплоте соответствующего превращения (плавле­ние, кипение, превращение из одной модификации в другую). На­конец, в случае химической реакции изменение энтальпии равно взятому с обратным знаком тепловому эффекту реакции, проведенной при постоянной температуре и постоянном давлении.

Энтальпия, как и внутренняя энергия, характеризует энергетическое состоя­ние вещества, но включает энергию, затрачиваемую на преодоление внешнего
давления, т. е. на работу расширения. Подобно внутренней энергии, энтальпия определяется состоянием системы и не зависит от того, каким путем это состояние достигнуто. В случае газов различие между Δ U и ΔНв ходе того или
иного процесса может быть значительным. В случае систем, несодержащих газов, изменения внутренней энергии (Δ U) и энтальпии (ΔН), сопровождающие процесс, близки друг к другу. Это объясняется тем, что изменения объема ( Δ V) при
процессах,претерпеваемых веществами в конденсированных (т.е. в твердом или в жидком) состояниях, обычно очень невелики, и величина РΔV мала в сравнении с АН.

Термодинамические величины. Энтропия и энергия Гиббса.

Как уже говорилось, макросостояние системы тем более вероятно, чем большим числом микросостояний оно может осуще­ствиться. Обычно число микросостояний, отвечающих тому или иному макросостоянию системы, очень велико. Это связано с тем, что в макроскопических количествах вещества число частиц колос­сально велико, а их положения и скорости при обычных темпера­турах чрезвычайно разнообразны.

Характеризовать в этом смысле состояние системы оказалось удобнее не самой вероятностью осуществления данного макросос­тояния, а величиной, пропорциональной ее логарифму. Эта вели­чина называется энтропией. Энтропия (S) связана с числом (W) равновероятных микроскопических состояний, которыми можно реализовать данное макроскопическое состояние системы, уравнением

S = k lg W, где k — коэффициент пропорциональности

Наименьшую энтропию имеют идеально правильно построенные кристаллы при абсолютном нуле. Энтропия кристалла, в струк­туре которого имеются какие-либо неправильности, уже при абсо­лютном нуле несколько больше, так как нарушения идеальности могут реализоваться не единственным способом. С повышением температуры энтропия всегда возрастает, так как возрастает ин­тенсивность движения частиц, а следовательно, растет число спо­собов их расположения. Возрастает она также при превращении вещества из кристаллического состояния в жидкое и, в особенно­сти, при переходе из жидкого состояния в газообразное. Изме­няется энтропия и при протекании химических процессов. Эти изменения обычно особенно велики в случае реакций, приводящих к изменению числа молекул газов: увеличение числа газовых мо­лекул приводит к возрастанию энтропии, уменьшение — к ее по­нижению.

Подобно внутренней энергии и энтальпии, энтропия зависит только от состояния системы. Но, в отличие от этих двух функций, связь изменения энтропии с теплотой зависит от способа проведе­ния процесса — от его скорости.

Как уже говорилось, в ходе того или иного процесса соотноше­ние между теплотой и производимой работой может быть различ­ным. Только разность этих величин, равная изменению внутрен­ней энергии системы, не зависит от способа осуществления про­цесса. При быстром его проведении работа бывает малой, а при медленном она возрастает. При бесконечно медленном осуществле­нии процесса — при проведении его бесконечно малыми шагами от одного состояния равновесия к следующему, бесконечно близкому к предыдущему, — работа принимает максимально возможное значение. Такое проведение процесса называется термодина­мически обратимым, или просто обратимым (Термодинамическую обратимость как способ проведения процесса не сле­дует путать с химической обратимостью - способностью реакции протекать и в прямом, и в обратном направлении).

В ряде случаев к обратимому проведению процесса можно приблизиться в экспериментальных условиях с высокой точностью. В лаборатории можно практически обратимо проводить окисли­тельно-восстановительные реакции в гальванических элементах (см. § 98), плавление твердого тела, испарение жидкости. Если процесс проводится обратимо и при постоянной темпера­туре (изотермически), то изменение энтропии связано с поглощаемой теплотой уравнением

ΔS = Q_o6р/Т,

где Q_o6p — количество теплоты, поглощенной системой в изотерми­ческом обратимом процессе; Т— абсолютная температура.

С помощью этого уравнения можно определить, например, из­менение энтропии при плавлении и кипении веществ.

Последнее уравнение показывает, что при поглощении некоторого количе­ства теплоты энтропия системы возрастает тем сильнее, чем ниже температура, при которой поглощается теплота. Это можно пояснить следующим образом. Подведем одно и то же количество теплоты к двум одинаковым порциям данного вещества. При этом пусть одна из порции находится при низкой темпера­туре, например 1 К, а другая — при высокой температуре, например 1000 К. Ясно, что относительное возрастание скорости движения частиц и увеличение степени их неупорядоченности, а следовательно, и возрастание энтропии в пер­вом случае будет больше, чем во втором.

Энтропия имеет размерность энергии, деленной на температу­ру; выражают ее обычно в Дж/К.

Как показывается в термодинамике, можно ввести такие функ­ции, которые отражают влияние на направление протекания про­цесса как тенденции к уменьшению внутренней энергии, так и тен­денции к достижению наиболее вероятного состояния системы. Знак изменения подобной функции при той или иной реакции может служить критерием возможности самопроизвольного проте­кания реакции. Для изотермических реакций, протекающих при постоянном давлении, такой функцией является энергия Гибб­с G, называемая также изобарно-изотермическим потенциалом, изобарным потенциалом или сво­бодной энергией при постоянном давлении. Джозайя Уиллард Гиббс (1839—1903)—выдающийся американский физик, один из основателей химической термодинамики и статистической

физики.

Энергия Гиббса связана с энтальпией, энтропией и температу­рой соотношением:

G = H -TS

Если реакция осуществляется при постоянных давлении и тем­пературе (такой процесс называется изобарно-изотермическим), то изменение энергии Гиббса при реакции будет равно:

ΔG = ΔН - TΔS

При обратимом и изотермическом проведении процесса AG равно по абсолютной величине, но обратно по знаку максималь­ной полезной работе, которую система производит в данном про­цессе:

ΔG = - А_макс

Полезной работой называется вся производимая в ходе про­цесса работа за вычетом работы расширения PΔV.

Можно показать, что в условиях постоянства температуры и давления реакции протекают самопроизвольно в сторону умень­шения энергии Гиббса. Поскольку ΔG равно по величине, но об­ратно по знаку максимальной полезной работе процесса, то сказанное можно сформулировать иначе: самопроизвольно могут протекать только те реакции, за счет энергии которых можно со­вершать полезную работу.

Для грубой оценки того, в каком направлении может протекать та или иная реакция при низких и при высоких температурах, можно воспользоваться приближенными уравнениями для измене­ния энергии Гиббса. При низких температурах множитель Т мал и абсолютное значение произведения TΔS тоже мало. В этом случае для реакций, имеющих значительный тепловой эффект, |ΔН|>>|TΔS|. Тогда в выражении

ΔG = ΔН - TΔS

вторым членом можно пренебречь. При этом получим

ΔG ≈ ΔН

При достаточно высоких температурах (множитель Т велик) имеем обратное соотношение:

|ΔН| << |TΔS|

Пренебрегая теперь первым членом в выражении энергии Гибб­са, получим

ΔG = - TΔS

Эти приближенные равенства показывают, что при низких тем­пературах критерием направления самопроизвольного протекания реакции в первом приближении может служить знак теплового эффекта реакции, а при высоких — знак изменения энтропии. Это означает, что при низких температурах самопроизвольно протекать могут экзотермические реакции, а при высоких — реакции, сопро­вождающиеся увеличением энтропии.

К сказанному необходимо добавить, что отрицательное значе­ние ΔGтой или иной реакции указывает именно только на возмож­ность ее протекания. В действительности реакция может при этом и не наблюдаться. Дело в том, что скорость ее может быть малой; тогда, несмотря на соблюдение условия ΔG< 0, реакция практи­чески не будет протекать. В этих случаях для увеличения скорости реакции необходимо подобрать катализатор. Такое положение осо­бенно часто наблюдается при низких температурах.

---

Дата добавления: 2015-08-21