Висновки. Отримавши дві незалежні вибірки записів раєстраторів

Отримавши дві незалежні вибірки записів раєстраторів, що записують відхилення в часі вихідного параметру системи від заданого значення, ми проаналізували їх за допомогою методів математичної статистики.

Спочатку ми наочно зобразили статистичний розподіл обох вибірок за допомогою гістограми. Для того, щоб гістограма не була громіздкою, ми згрупували ряд по частковим інтервалам. Далі були знайдені точкові оцінки математичних сподівань і дисперсій генеральних сукупностей за допомогою метода найбільшої правдоподібності. Обчислення велися методом добутків. Знайдені значення дисперсії є мірою відхилення значень випадкової величини від середнього, а моменти - числова характеристика розподілу даних виборок. Інтервальні оцінки, що визначаються двома кінцями інтервалу даних вибірки, були представлені в роботі знаходженням невідомого математичного спордівання за допомогою довірчого інтервалу із вказаною надійністю. Після цього була перевірена гіпотеза про рівність дисперсій двох генеральних сукупностей. В результаті дослідження, було з’ясовано, що нульова гіпотеза справедлива, тобто генеральні дисперсії однакові, відмінність „виправлених” дисперсій незначуща, і може бути пояснена випадковими причинами.

Були визначені емпіричні і вирівнюючі частоти виборки, і за допомогою них побудовані нормальні криві і полігони частот. Для порівняння обидві криві кожної множини були розміщені на одному графіку, який показав, що побудована теоретична крива задовільно відображає результати спостережень.

Для перевірки гіпотези про нормальний розподіл сукупностей був знайдений критерій узгодженості Пірсона. За результатами розрахунків було вияснено,що для множини Х є підстави відхилити нульову гіпотезу, а для множини Y немає підстав відхилити нульову гіпотезу, тобто розходження емпіричних та теоретичних частот несуттєве для множини Y.

Перевірка гіпотез про рівність нулю генеральних середніх нормальних генеральних сукупностей дала позитивний результат. Обчислення показали, що немає підстав відхилити нульову гіпотезу, тобто вибіркове середнє незначуще відрізняється від гіпотетичної генеральної середньої.

Для оцінки відхилення емпіричного розподілу від нормального були знайдені такі характеристики, як асиметрія і ексцес. В обох виборках полігон варіаційного ряду асиметричний, причому коефіцієнт асиметрії від’ємний, тобто плавніший „спуск” полігону частот спостерігається зліва. Знайдені значення ексцесу для обох виборок виявилися додатними, що вказує на те, що полігони мають загострену вершину порівнянно із нормальною кривою.

Тепер маючи всі значення можемо побудувати математичну модель за формулою 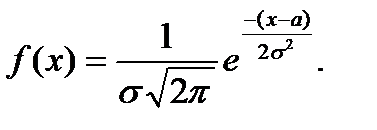Криву Гауса будую за допомогою MS Excel.

Математична модель для вибірки X зображена на рис. 5:

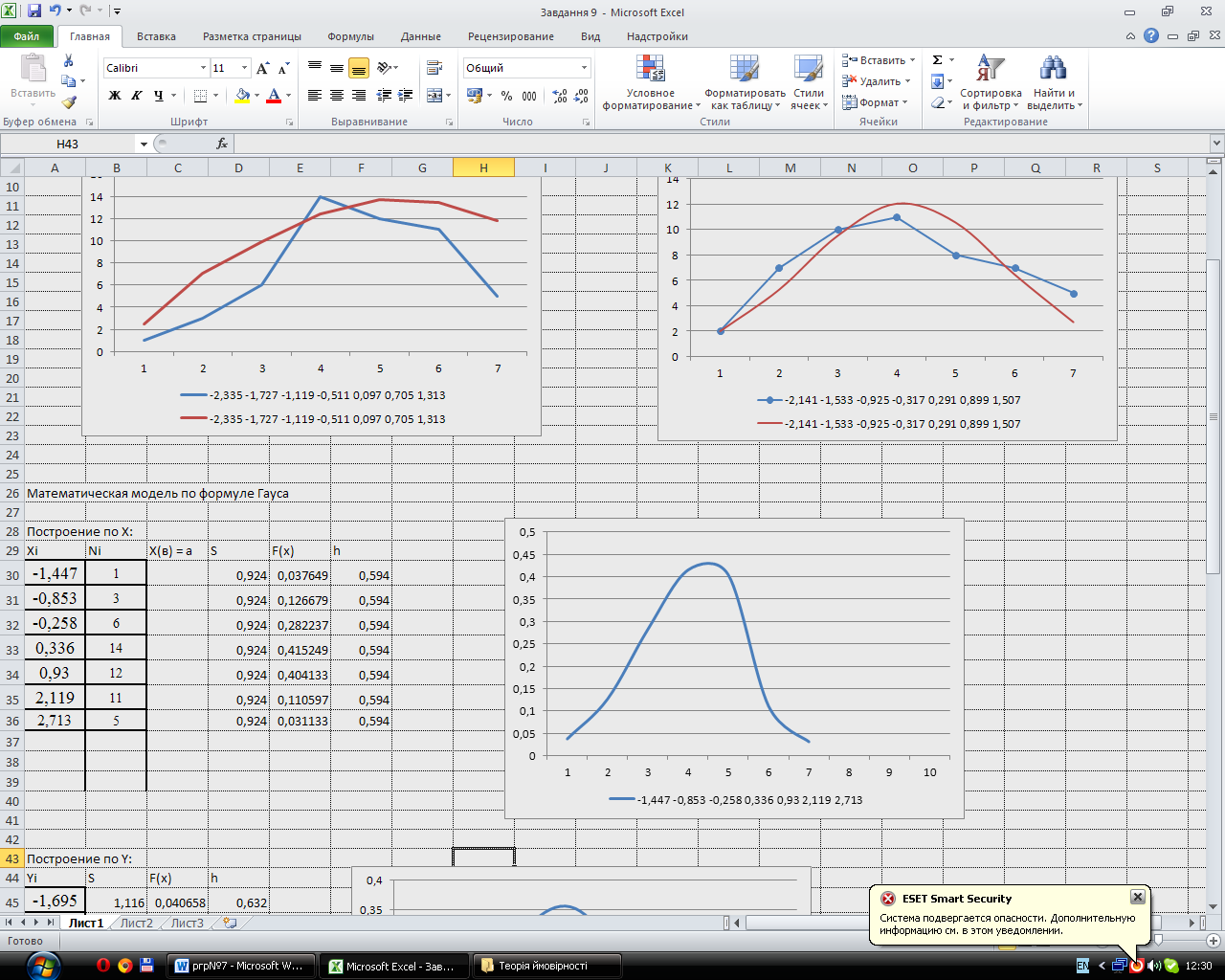
Рис. 5 Математична модель для вибірки Х

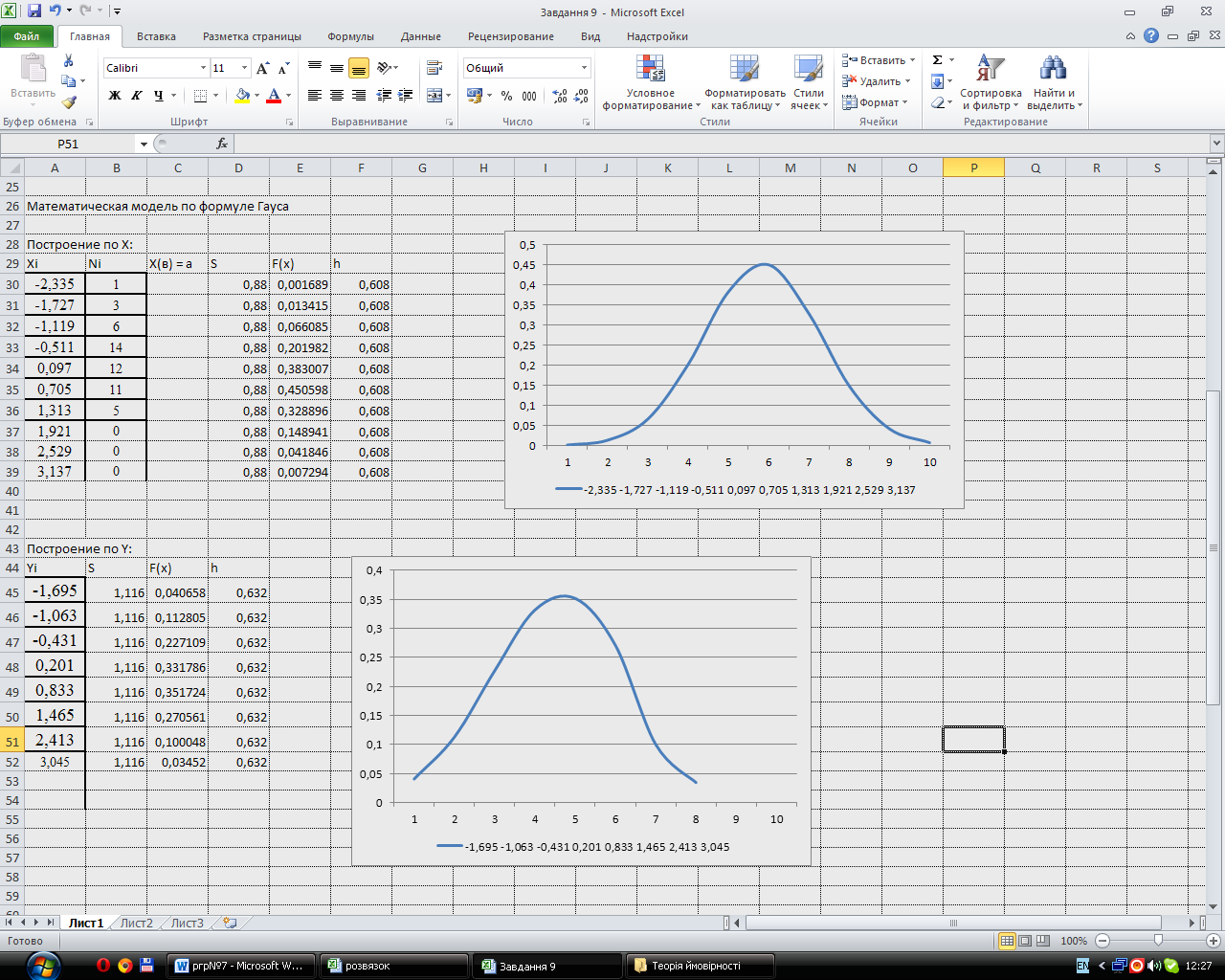Математична модель для вибірки Y зображена на рис. 6:

Рис. 6 Математична модель для вибірки Y

Дата завершення роботи - 30.11.2011р.

Дата добавления: 2015-08-21