Потужність у колі змінного струму

Миттєве значення потужності дістанемо, перемноживши миттєві значення ЕРС і сили струму:

Одержане значення потужності в певні моменти часу перетворюється на нуль. Нас цікавить середнє значення потужності за період

Значення другого члена у рівнянні за період буває як додатним, так і від'ємним, тому середнє значення за період цього члена дорівнює нулю. Перший член не залежить від часу, тому його середнє значення за період дорівнює йому самому.

Отже, середнє значення потужності змінного струму за період:

Якщо розглядати поняття про ефективні значення ЕРС, сили струму, напруги:

Якщо зсув фаз ф = 0 (наприклад, у разі дії лише активного опору), то

Отже, ефективні значення ЕРС, сили струму (і напруги) відіграють таку саму роль, що й ЕРС та сила струму за постійного струму.

Знайдемо кількість теплоти, що виділяється в колі змінного струму:

Тут ще раз впевнюємося в тому, що індуктивний опір у процесі виділення тепла в колі змінного струму (як і ємнісний) безпосередньої участі не бере. Тому індуктивний і ємнісний опори й дістали назву реактивних опорів.

Ефективні значення електрорушійної сили, сили струму і напруги в колах змінного струму відіграють таку саму роль, як і відповідні величини в колах постійного струму

Індуктивний і ємнісний опори у процесі виділення тепла участі не беруть, тому й називаються реактивними

За наявності зсуву фаз між ЕРС і силою струму корисно споживана потужність залежить від , тому величину ще називають коефіцієнтом потужності. Щоб ефективність використання енергії в лініях була високою, потрібно збільшувати coscp. Цього можна досягти у двох випадках: маючи лише активні навантаження, що не завжди можливо, або ж якимось способом компенсуючи дію реактивних опорів, які лише збільшують силу струму в лініях (а отже, і втрати енергії в них). Розглянемо спільну дію індуктивного та ємнісного опорів у колі змінного струму, що дасть змогу знайти шляхи підвищення ефективності використання електричної енергії.

Найпростішими електричними ланцюгами, у яких може постати резонанс, є послідовне і паралельне сполуки резистора, індуктивності і ємності. Відповідно схемою сполуки, ці ланцюга називаються послідовним і паралельним резонансним контуром. Наявністьрезистивного опору в резонансному контурі з визначення перестав бути обов'язковим і може відсутні як елемент (резистор). Проте за аналізірезистивним опором треба враховувати по крайнього заходу опору провідників.

53.

Колива́льний ко́нтур або коливний контур — електричне коло, складене з резистора, ємності та індуктивності, в якому можливі коливання напруги й струму. Коливальні контури широко застосовуються в радіотехніці та електроніці, зокрема в генераторах електричних коливань, в частотних фільтрах. Вони використовуються практично в кожному електротехнічному пристрої.

Послідовний RLC-коливальний контур:

v - джерело напруги

i - сила струму через контур

R - резистор в

L - індуктивність

C – ємність

Коливальний контур, що складається із послідовно з'єднаних індуктивності , ємності та активного резистора 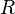називається RLC-контуром.

В загальному випадку активний опір 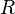включає не тільки активні опори провідників, а й опір, зв'язаний з витратами на випромінювання, що виникає внаслідок відкритості конденсатора та індуктивності.

У випадку, коли активний опір малий, і ним можна знехтувати, коливальний контур називаю LC-контуром.

В ланку коливального контура можна добавити перемикач для аналізу процесу накопичення зарядів на ємності.

Коливальний контур, що складається із послідовно з'єднаних індуктивності L \, ємності C \ та активного резистора R \ називається RLC-контуром.

В загальному випадку активний опір R включає не тільки активні опори провідників, а й опір, зв'язаний з витратами на випромінювання, що виникає внаслідок відкритості конденсатора та індуктивності.

У випадку, коли активний опір малий, і ним можна знехтувати, коливальний контур називаю LC-контуром.

В ланку коливального контура можна добавити перемикач для аналізу процесу накопичення зарядів на ємності.

Формула Томсона названа в честь английского физика Уильяма Томсона, который вывел её в 1853 году, и связывает период собственных электрических колебаний в контуре с его ёмкостью и индуктивностью.^[1]

Формула Томсона выглядит следующим образом^[2]:

.

Вимушеними називаються коливання, що відбуваються під дією періодичної зовнішньої сили. Щоб у реальній коливальній системі отримати незатухаючі коливання, треба компенсувати втрати енергії. Така компенсація можлива за допомогою якого-небудь періодичного чинника х(t), який змінюється за гармонійним законом:

• ,

де — частота.

Для вимушених коливань характерне явище резонансу — значне збільшення амплітуди коливань тоді, коли частота збурення збігається із одною з власних частот коливної системи.

Затухаючі коливання - коливання, енергія яких зменшується з часом. Нескінченно що триває процес виду в природі неможливий. Вільні коливання будь-якого осцилятора рано чи пізно загасають і припиняються. Тому на практиці звичайно мають справу з затухаючими коливаннями. Вони характеризуються тим, що амплітуда коливань A є спадною функцією. Зазвичай загасання відбувається під дією сил опору середовища, найбільш часто висловлюються лінійною залежністю від швидкості коливань або її квадрата.

54. Резона́нс — явище сильного зростання амплітуди вимушеного коливання у разі, коли частота зовнішньої сили збігається з власною частотою коливань.

Резонанс характеризують інтенсивністю, напівшириною спектральної лінії та добротністю. Здебільшого резонанс наближено описують кривою Лоренца

,

де ω — частота зовнішньої сили, ω₀ — частота власного коливання, Γ — стала затухання, яку називають також шириною лінії. Часто приводиться також γ= Γ/2 — півширина лінії.

Явище резонансу широко використовується в науці й техніці. На ньому ґрунтується робота багатьох радіотехнічних схем та пристроїв, таких як коливні контури. Використовуючи явище резонансу ми вибираємо із багатого різноманіття електромагнітних хвиль в просторі навколо нас саме ті, які відповідають нашій улюбленій радіостанції, вибираємо телевізійний канал тощо.

Проте не завжди резонанс корисний. Відомі випадки, коли навісні мости ламалися при проходжені по ним солдат "в ногу". Це відбувалося через те, що частота власних коливань полотна моста збігалася з частотою ходи людей.

Перейти до: навігація, пошук

Декремент затухання - величина, яка визначає швидкість зменшення амплітуди гармонічних коливань з часом при затуханні.

Коли гармонічні коливання затухають, значення змінної u, що їх описує, в момент часу t задається формулою

.

Тут - коефіцієнт затухання, - амплітуда в початковий момомент часу, - частота коливань.

Коефіцієнт затухання має розмірність оберненого часу. Безрозмірна величина , де - період коливань називається логарифмічним декрементом затухання або просто декрементом затухання.

Величина декремента затухання для реальної коливної системи визначається властивими їй процесами дисипації енергії.

Добротність коливальної системи – величина, яка показує у скільки разів амплітуда вимушених коливань системи при резонансі перевищує амплітуду коливань при його відсутності.

Добротність котушки індуктивності - Добротність коливального контура визначається головним чином добротністю котушки індуктивності:

Q = wL_k/r_k,

яка залежить від багатьох причин.

Частина енергії магнітного поля котушки індуктивності витрачається на нагрівання провідника, тому більшу добротність мають котушки, намотані спеціальним багатожильним проводом - літцендратом. Деяка частина магнітного потоку розсіюється, не замикаючись на витки котушки. Застосовуючи магнітні сердечники, цього можна уникнути і зменшити кількість витків, отже, підвищити її добротність. на добротність котушки впливає також матеріал каркасу. Найменші втрати енергії дають каркаси, виготовлені з матеріалу, що характеризується високими діелектричними властивостями, наприклад з високочастотної кераміки (радіофарфор, радіостеатит), високомолекулярних матеріалів (полістирол, преспорошки). Нижчу добротність мають котушки, намотані на дерев"яних каркасах, каркасах з гетинаксу, картону або текстоліту.

55.58.Дифракціяхвиль — це явище огинання хвилями країв неоднорідностей на шляху хвиль. Для світлових хвиль дифракція — це потрапляння світла в ділянки геометричної тіні.

Дифракція чітко виявляється у випадку, коли розміри неоднорідності (наприклад, отвору) сумірні з довжиною хвилі (а). Якщо ж розміри завеликі, вона спостерігається лише на великих відстанях від неоднорідності (б).
Дифракційна ґратка (пристрій для вивчення закономірностей дифракції, дослідження спектрів і вимірювання довжин світлових хвиль) являє собою сукупність великого числа вузьких щілин однакової ширини, відокремлених непрозорими проміжками теж однакової ширини. (Принцип виготовлення сучасних ґраток такий: на загальному непрозорому фоні скла, вкритого тонким шаром алюмінію, мікрорізцем прорізують вузькі «вікна».)
Різні за якістю дифракційні ґратки мають від 300 до 1200 штрихів на міліметр (скла чи алюмінієвого покриття). Сума ширини прозорої ділянки ґратки і ширини непрозорої ділянки — це стала дифракційної ґратки d.
Формула дифракційної ґратки , де — ціле число.

Світлова картина, яка утворилась би при використанні однієї щілини, була б суто дифракційною, а при використанні ґратки утворюється інтерференційна картина як наслідок накладання променів від різних щілин. Отже, даний вираз відповідає умові, якій має задовольняти різниця ходу інтерферуючих променів для утворення інтерференційного максимуму. 

56. Принцип Гюйгенса — Френеля является развитием принципа, который ввёл Христиан Гюйгенс в 1678 году: каждая точка поверхности, достигнутая световой волной, является вторичным источником световых волн. Огибающая вторичных волн становится фронтом волны в следующий момент времени. Принцип Гюйгенса объясняет распространение волн, согласующееся с законами геометрической оптики, но не может объяснить явлений дифракции. Огюстен Жан Френель в 1815 году дополнил принцип Гюйгенса, введя представления о когерентности и интерференции элементарных волн, что позволило рассматривать на основе принципа Гюйгенса — Френеля и дифракционные явления.

Принцип Гюйгенса — Френеля формулируется следующим образом:

Каждый элемент волнового фронта можно рассматривать, как центр вторичного возмущения, порождающего вторичные сферические волны, а результирующее световое поле в каждой точке пространства будет определяться интерференцией этих волн.

Густав Кирхгоф придал принципу Гюйгенса — Френеля строгий математический вид, показав, что его можно считать приближенной формой теоремы, называемой интегральной теоремой Кирхгофа (см. метод Кирхгофа).

Фронтом волны точечного источника в однородном изотропном пространстве является сфера. Амплитуда возмущения во всех точках сферического фронта волны, распространяющейся от точечного источника, одинакова.

Дальнейшим обобщением и развитием принципа Гюйгенса — Френеля является формулировка через интегралы по траекториям, служащая основой современной квантовой механики.

Зони Френеля, ділянки, на які можна розбити поверхню світлової (або звуковий) хвилі для обчислення результатів дифракція світла (або звуку). Вперше цей метод застосував О. Френель в 1815—19. Суть методу така. Хай від точки Q (мал.), що світиться, поширюється сферична хвиля і потрібно визначити характеристики хвилевого процесу, викликаного нею в точці Р. Розділимо поверхню хвилі S на кільцеві зони; для цього проведемо з точки Р сфери радіусами PO, Ра = PO + ^l / ₂ ; Pb = Ра + ^l / ₂ , Pc = Pb + ^l / ₂ (Про — точка пересічення поверхні хвилі з лінією PQ; l — довжина світлової хвилі). Кільцеподібні ділянки поверхні хвилі, що «вирізуються» з неї цими сферами, і називається З. Ф. Волнової процес в точці Р можна розглядати як результат складання коливань, що викликаються в цій точці кожної З. Ф. окремо. Амплітуда таких коливань повільно убуває із зростанням номера зони (відлічуваного від крапки Про), а фази коливань, що викликаються в Р суміжними зонами, протилежні. Тому хвилі, що приходять в Р від двох суміжних зон гасять один одного, а дія зон, наступних через одну, складається. Якщо хвиля поширюється, не зустрічаючи перешкод, то, як показує розрахунок, її дія (сума дій всіх З. Ф.) еквівалентна дії половини першої зони. Якщо ж за допомогою екрану з прозорими концентричними ділянками виділити частини хвилі, відповідні, наприклад, N непарним зонам Френеля, та дія всіх виділених зон складеться і амплітуда коливань U _{непарне число} в точці Р зросте в 2n раз, а інтенсивність світла в 4 N ² разів, причому освітленість в крапках, що оточують Р, зменшиться. То ж вийде при виділенні лише парних зон, але фаза сумарної хвилі U _пар матиме протилежний знак. Такі зонні екрани (т.з. лінзи Френеля) знаходять вживання не лише в оптиці, але і в акустиці і радіотехніці — в області досить малих довжин хвиль, коли розміри лінз виходять не дуже великими (сантиметрові радіохвилі, ультразвукові хвилі). Метод З. Ф. дозволяє швидко і наочно складати якісне, а інколи і досить точне кількісне уявлення про результат дифракції хвиль за різних складних умов їх поширення. Він застосовується тому не лише в оптиці, але і при вивченні поширення радіо- і звукових хвиль для визначення ефективної траси «світивши», що йде від передавача до приймача; для з'ясування того, чи за даних умов гратимуть роль дифракційні явища; для орієнтування в питаннях про спрямованість випромінювання, фокусування хвиль і т.п.

57. 1. Дифракция на круглом отверстии. Сферическая волна, распространяющаяся из точечного источника S, встречает на своем пути экран с круглым отверстием. Дифракционную картину наблюдаем на экране Э в точке В, лежащей на линии, соединяющей S с центром отверстия (рис. 259). Экран параллелен плоскости отверстия и находится от него на расстоянии b. Разобьем открытую часть волновой поверхности Ф на зоны Френеля. Вид дифракционной картины зависит от числа зон Френеля, открываемых отверстием. Амплитуда результирующего колебания, возбуждаемого в точке В всеми зонами (см. (177.1) и (177.6)),

где знак плюс соответствует нечетным m и минус — четным т.

Когда отверстие открывает нечетное число зон Френеля, то амплитуда (интенсив­ность) в точке В будет больше, чем при свободном распространении волны; если четное, то амплитуда (интенсивность) будет равна нулю. Если отверстие открывает одну зону Френеля, то в точке В амплитуда А=А ₁, т. е. вдвое больше, чем в отсутствие непрозрачного экрана с отверстием. Интенсивность света больше соответственно в четыре раза. Если отверстие открывает две зоны Френеля, то их действия в точке В практически уничтожат друг друга из-за интерференции. Таким образом, дифракционная картина от круглого отверстия вблизи точки В будет иметь вид чередующихся темных и светлых колец с центрами в точке В (если т четное, то в центре будет темное кольцо, если m нечетное — то светлое кольцо), причем интенсивность в максимумах убывает с расстоянием от центра картины.

Расчет амплитуды результирующего колебания на внеосевых участках экрана более сложен, так как соответствующие им зоны Френеля частично перекрываются непроз­рачным экраном. Если отверстие освещается не монохроматическим, а белым светом, то кольца окрашены.

Число зон Френеля, открываемых отверстием, зависит от его диаметра. Если он большой, то А_m << A ₁ и результирующая амплитуда A=A ₁ / 2, т. е. такая же,как и при полностью открытом волновом фронте. Никакой дифракционной картины не наблю­дается, свет распространяется,как и в отсутствие круглого отверстия, прямолинейно.

2. Дифракция на диске. Сферическая волна, распространяющаяся от точечного источника S, встречает на своем пути диск. Дифракционную картину наблюдаем на экране Э в точке В, лежащей на линии, соединяющей S с центром диска (рис. 260). В данном случае закрытый диском участок волнового фронта надо исключить из рассмотрения и зоны Френеля строить начиная с краев диска. Пусть диск закрывает m первых зон Френеля. Тогда амплитуда результирующего колебания в точке В равна

или

так как выражения, стоящие в скобках, равны нулю. Следовательно, в точке В всегда наблюдается интерференционный максимум (светлое пятно), соответствующий поло­вине действия первой открытой зоны Френеля. Центральный максимум окружен концентрическими с ним темными и светлыми кольцами, а интенсивность в максимумах убывает с расстоянием от центра картины.

С увеличением радиуса диска первая открытая зона Френеля удаляется от точки В и увеличивается угол j_т (см. рис. 258) между нормалью к поверхности этой зоны и направлением на точку В. В результате интенсивность центрального максимума с увеличением размеров диска уменьшается. При больших размерах диска за ним наблюдается тень, вблизи границ которой имеет место весьма слабая дифракционная картина. В данном случае дифракцией света можно пренебречь и считать свет распространяющимся прямолинейно.

Отметим, что дифракция на круглом отверстии и дифракция на диске впервые рассмотрены Френелем.

Дата добавления: 2015-08-21