Другий закон

Другий закон Кірхгофа (Закон напруг Кірхгофа, ЗНК) говорить, що алгебраїчна сума падінь напружень по будь-якому замкнутому контуру кола дорівнює алгебраїчній сумі ЕРС, що діють уздовж цього ж контура. Якщо в контурі немає ЕРС, то сумарне падіння напруги дорівнює нулю:

для постійних напруг

для змінних напруг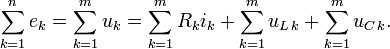

Іншими словами, при обході ланцюга по контуру, потенціал, змінюючись, повертається до початкового значення. Якщо ланцюг містить гілок, з яких містять джерела струму гілки в кількості , То вона описується рівняннями напруг. Окремим випадком другого правила для ланцюга, що з одного контуру, є закон Ома для цього ланцюга.

Закони Кірхгофа справедливі для лінійних і нелінійних ланцюгів при будь-якому характері зміни в часі струмів і напруг.

Приклад

На цьому малюнку для кожного провідника позначений протікає по ньому струм (буквою "I") і напруга між сполучаються їм вузлами (буквою "U")

Наприклад, для наведеної на малюнку ланцюга, відповідно до першого закону виконуються наступні співвідношення:

Зверніть увагу, що для кожного вузла має бути вибрано позитивний напрямок, наприклад тут, струми, що впадає у вузол, вважаються позитивними, а випливають - негативними.

Згідно з другим законом, справедливі співвідношення:

Закон випромінювання Кирхгофа - відношення випромінювальної здатності будь-якого тіла до його поглинальної здатності однакове для всіх тіл при даній температурі для даної частоти для рівноважного випромінювання і не залежить від їх форми, хімічного складу та ін.

Закон Стефана-Больцмана дає залежність енергії випромінювання з одиниці площі поверхні в одиницю часу від ефективної температури тіла, що випромінює.

Загальна енергія теплового випромінювання визначається як:

,

де — потужність на одиницю площі поверхні випромінювання, а

Вт/(м²·К⁴) — стала Стефана—Больцмана.

Закон зміщення Віна дає залежність довжини хвилі, на якій потік випромінювання енергії чорного тіла сягає свого максимуму, від температури чорного тіла.

Дата добавления: 2015-08-21