Доведення закону

Для доведення можна використати вираз закону випромінювання Планка для абсолютно чорного тіла, записаного для довжин хвиль:

Щоб знайти екстремуми цієї функції в залежності від довжини хвилі, її слід продиференціювати по й прирівняти диференціал до нуля:

З цієї формули відразу можна визначити, що похідна наближається до нуля коли 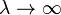чи коли , що справджується при 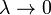. Проте, обидва ці випадки дають мінімум функції Планка 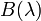, яка для зазначених довжин хвиль сягає свого нуля (див. малюнок угорі). Тому аналіз слід продовжити лише з третім можливим випадком коли

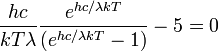
Використовуючи заміну змінних , дане рівняння можна перетворити на

Чисельний розв'язок цього рівняння дає ^[1]:

Таким чином, враховуючи заміну змінних та значення сталих Планка, Больцмана та швидкості світла, довжина хвилі, на якій інтенсивність випромінювання абсолютно чорного тіла сягає свого максимуму, визначається як

,

де температура задана в кельвінах, а — у метрах.

радіодіапазону.

68. Фото́н (грец. Φωτόνιο)— квант електромагнітного поля, елементарна частинка, що є носієм електромагнітної взаємодії.

Дата добавления: 2015-08-21