Обобщение структур, заданных в виде жизненных циклов

Потоки данных в крупных информационных системах огромны и часто содержат в себе больше знаний, чем это видно на первый взгляд. Анализ и поиск закономерностей в больших объемах информации - задача актуальная и сложная. Качество программного продукта в этом случае во многом зависит от опыта человека, разрабатывающего программу. Одной из задач, стоящих перед таким специалистом, является обобщение структур, составляющих предметную область. Предметную область можно представить как дискретное пространство координат D. Каждая координата xi является характерным признаком исследуемой области, где i=1,n. Вдоль оси хi отложены значения хi ={хij}, где j=1,ki, ki - число значений по координате хi. Объекты в пространстве D представлены векторами X=, где ai - значение по координате хi. В пространстве D определяют два набора векторов примеров: T - положительные, F - отрицательные. По выборке примеров T, F строят функцию выбора

Y(X)= 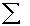xij*Cij+Co,

где хij - j-е значение i-й координаты, Cij - весовой коэффициент при j-ом значении i-й координаты, C0 - порог функции выбора (ФВ).

Значения Cij определяют из условия y(X)>=0 при X є T и y(X)<0 при X є F для всей обучающей выборки. Цикл обучения замыкается процессом выдвижения гипотез, которые эксперт должен оценить на качественном уровне. Гипотезы экспертная система выбирает среди вариантов, расположенных на границе разделения y[u](X)=0, где u - номер цикла обучения. Гипотезы, определенные человеком как положительные примеры, дополняют множество T до обучающей выборки, а отрицательные дополняют множество F.

В случае с созданием структуры бизнес-плана ее можно представить в виде ряда схем.

2.1 Структурная модель

2.2 Модель пространства

Расстояние между характерними точками рассчитывается по формуле:

где кх=1, ку=1 - весовые коэффициенты х и у.

Исходя из формулы условие существования пространственной связи (между характерними точками) d1<=1.

2.2.1 Модель пространства уровня простой заявки

Пространственные связи

среда.Хт1 <а fo.Хт3

среда.Хт2 Я> Поку.Хт4

2.2.2 Модель пространства уровня расширенной заявки

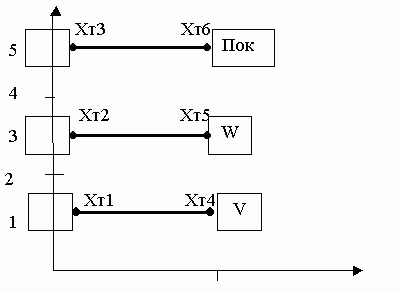
Пространственные связи:

среда.Хт1 Я> V.Хт4

среда.Хт2 Я> W.Хт5

среда.Хт3 Я> Пок.Хт6

2.2.3 Модель пространства уровня бизнес-плана

Пространственные связи

среда.Хт1 Я> Пок.Хт6

среда.Хт2 Я> W.Хт7

среда.Хт3 Я> V.Хт8

среда.Хт4 Я> SD.Хт9

среда.Хт8 Я> K.Хт10

SD.Хт11 Я> K.Хт12

SD.Хт13 Я> CV.Хт15

K.Хт14 Я> CV.Хт16

2.3 Декомпозиция характерных точек на свойства

2.4 Декомпозиция блока Wу в пространстве и времени

Уровень расширенной заявки: Wу = Rt*Vt

Уровень бизнес-плана:

У блоков разные координаты, например у блока Wу координаты (1;3). После декомпозиции блока я ввела дополнительную ось времени (t). Например координаты подблока Wt=3 будут равны (1;3;3).

Поскольку проделана декомпозиция блока на подблоки, возникает необходимость различать подблоки 2-го уровня в пространстве. Я ввела дополнительную ось Z. И, например подблок 2-го уровня подблока Wt=3 получил координати (1;3;2;3). Альтернативное решение данной структури: возможно вводить разные значения лет и других показателей. Таким образом, строится множество жижизненных циклов (прототипов) как история поведения объектов во времени. Для любого подблока можнр получить обобщенную таблицу возможных комбинаций его свойств во времени и определить ее как функцию. Далее процесс моделирования складывается:

- в задании начальных условий для моделирования.

- в сужении при помощи функций начальних условий на все стороны.

Аналог роботы с недоопределенными вычислительными моделями описан у Нариньяни А. С. Особенностью роботы является введение нечисленного набора сложных примеров. Для автоматизации процесса описания сложных решений применяется аппарат изобретений, который, комбинируя подмножества структур разных прототипов может породить новое решение и предложить пользователю для проверки его достоверности.

3 Роль И/ИЛИ- дерева как аппарата представления базы знаний

Базой знаний в системе является:

- И/ИЛИ- дерево, т.е. упорядоченная множество синтермов по И и по ИЛИ, причем все синтермы имеют адрес в И/ИЛИ- дереве;

- Множество семантических двунаправленных зависимостей между ИЛИ- синтермами, что описывают их совместимость между собой, т.е. правил вывода или продукций.

Представление данных в виде И/ИЛИ дерева необходимо для выполнения теоретико-множественных операций над базой знаний системы в процессе обучения и вывода. Поиск решений в системе ведется по И/ИЛИ дереву, которое состоит из единиц информации поданных некоторой структурой. Под И/ИЛИ деревом понимается некоторый граф не содержащий циклов и имеющий ветвистую иерархическую многоуровневую структуру. Вершинами этого дерева или узлами некоторых поддеревьев являются термы и синтермы. Термом называется элементарный символ множества. Термы соединяются между собой только при помощи операции "И" (&). Синтермом называется имя множества, которое может разлагаться на составные части. Элементами разложения могут быть как термы, так и синтермы, соединенные при помощи операции "И" (&) или "ИЛИ" (V). Очевидно, что термы будут быть только письмами дерева, что, не могут иметь "сыновей" в данном дереве.

1. Особенности переходов между уровнями знаний

При переходах между уровнями возникает проблема переноса знаний с верхнего на нижний уровень. Другими словами, всякое свойство, принадлежащее некоторому уровню l, должно иметь соответствие на нижележащем уровне l'. Из этого ограничения можно вывести следующие следствия:

1. Недопустимым является замена одного из базовых свойств уровня знаний l некоторым новым свойством на уровне знаний l'.

2. Недопустимо удаление любого базового свойства уровня l при переходе на уровень l'.

3. Допустимой формой изменения состава базовых свойств уровня l относительно уровня l' является только декомпозиция свойств или значений.

Исходя из первого следствия, можно утверждать, что на стыке двух смежных уровней представления знаний всегда выполняется равенство, количество базовых свойств нижнего и верхнего уровня соотносятся одинаково. Рассмотрим возможные формы перехода набора базовых элементов первого уровня в набор элементов первого уровня неполноты информации для нижележащего уровня представления знаний. Формы перехода классифицируем следующим образом:

1. По набору свойств:

1.1. Определение структуры для базового элемента - "прочие не определенные свойства" уровня представления знаний l, то есть введение новых свойств на уровне l посредством декомпозиции.

1.2. Перенос базового, но неопределенного (то есть не имеющего определенного списка значений) свойства в разряд не базовых свойств, то есть не имеющих определенной структуры с последующим заданием новых свойств при декомпозиции.

2. По значениям свойств:

2.1. Определение значений для базовых неопределенных свойств, то есть декомпозиция значения "не доопределенное значение" для некоторого свойства.

2.2. Доопределение множества значений для базовых определенных свойств, то есть декомпозиция значения "не доопределенное значение" для некоторого свойства.

Дата добавления: 2015-08-21