Завдання. Математичний факультет

Математичний факультет

Кафедра прикладної математики

Дисципліна: методи оптимізації

З В І Т

з лабораторної роботи № 10-11

Тема: “ Методи штрафних функцій для задач умовної оптимізації”

студента 3-го курсу спеціальності «Прикладна математика»

Берліна Олексія Григоровича

________________

(Підпис студента)

Оцінка __________________

Перевірено ______________

(Дата)

Викладач ________________ /________________/

(Підпис) (Прізвище та ініціали)

Черкаси – 2013 р.

Завдання

1. Для задач одновимірної мінімізації записати бар’єрні функції 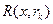виду

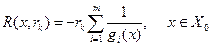
і відповідні їм функції при

1) ;

2) ;

3) ;

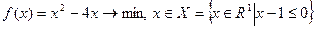4) ;

5) .

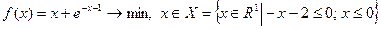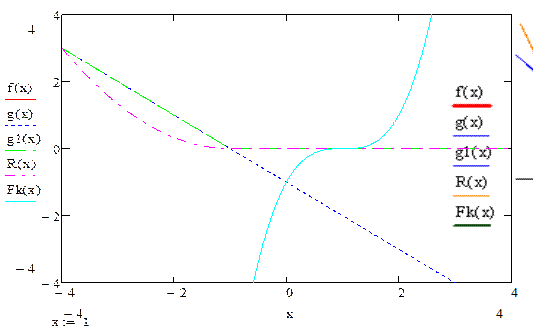
За допомогою програмних засобів типу Advanced Grapher, Derive, GRAN1, Mathcad, Matlab, Maple, Mathematica чи інших побудувати графіки функцій 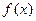, , 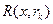, , і знайти розв’язки поставлених задач (див. приклад 1).

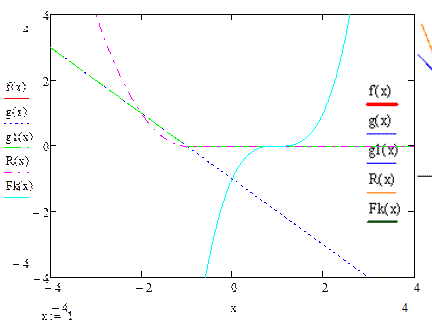
1) ;

Бар’єрна функція 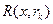(1)

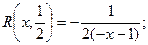
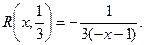
Бар’єрна функція (2)

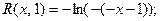
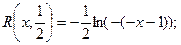
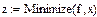
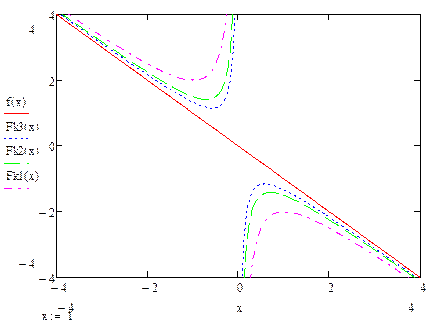
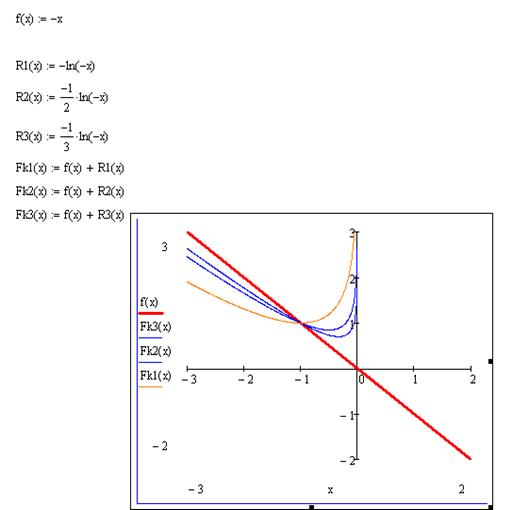
2) ;

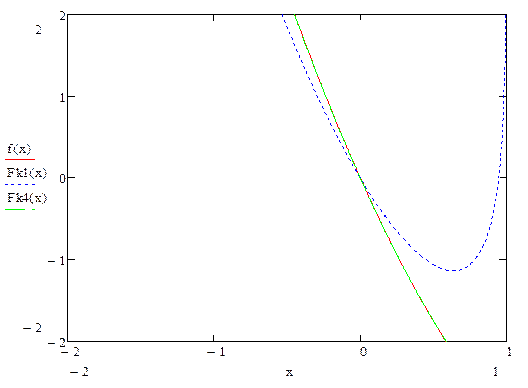
3)

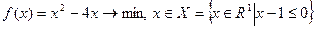
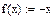
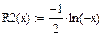
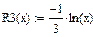
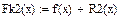
3)

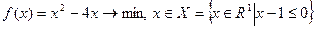
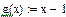
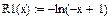
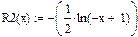
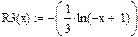
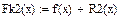
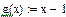
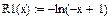
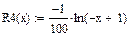
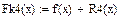
4)

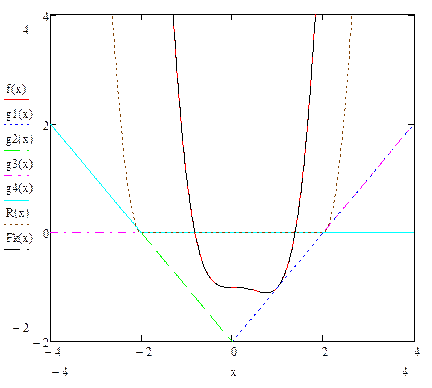
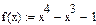
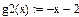
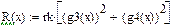
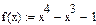
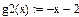
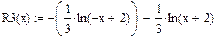
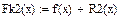
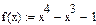
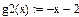
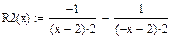
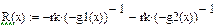
5)

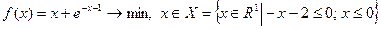
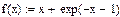
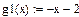
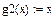
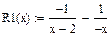
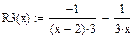
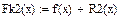
2)За методом бар’єрних функцій знайти розв’язки задач, використовуючи функції

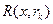1. виду (21), (22) при (див. приклад 2):

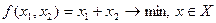, де ;

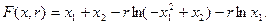
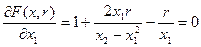
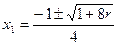
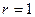
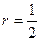
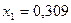
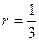
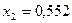
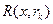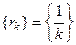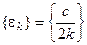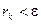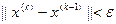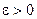3) Однією з мов програмування описати алгоритм роботи за методом бар’єрних функцій (29)-(31) з бар’єрними функціями виду (25)-(28), поклавши, наприклад, , , де . Ітераційний процес завершувати при виконанні однієї з умов або , – парне число, де – параметр точності обчислень.

Розвязок:

Метод внутрішніх штрафних функцій:

function barrier_shtraf_func1(f,g,x0,e)

[m,n]=size(g);

G='';

p=g(1,:);

%G=['1/(',p,')'];

G=['log(-(',p,'))'];

for i=2:m

p=g(i,:);

%G=[G,'+1/(',p,')'];

G=[G,'+log(-(',p,'))'];

end;

G=['(',G,')'];

flag=0;

k=0;

x_old=[0 0];

f_old=0;

F='';

while flag==0

k=k+1;

r=1/k;

F=[f,'-',num2str(r),'*',G];

%[xk]=fminsearch(F,x0);

[xk]=fminunc(F,x0);

x=xk;

fmin=eval(f);

if k~=1

norma=((x_old(1)-xk(1))^2+(x_old(2)-xk(2))^2)^(1/2);

%norma=abs(x_old-xk);

if r<e

flag=1;

end;

if norma<e

flag=1;

end;

if abs(f_old-fmin)<e

flag=1;

end;

end;

x_old=xk

f_old=fmin

k

end;

xk

fmin

k

Метод зовнішніх штрафних функцій:

function zovn_shtraf_func1(f,g,x0,p1,e)

[m,n]=size(g);

G='';

p=g(1,:);

G=['(max(0,',p,'))^',num2str(p1)];

for i=2:m

p=g(i,:);

G=[G,'+(max(0,',p,'))^',num2str(p1)];

end;

G=['(',G,')'];

flag=0;

k=0;

x_old=[0 0];

f_old=0;

F='';

while flag==0

k=k+1;

r=k^2;

F=[f,'+',num2str(r),'*',G];

[xk]=fminsearch(F,x0);

x=xk;

fmin=eval(f);

if k~=1

norma=((x_old(1)-xk(1))^2+(x_old(2)-xk(2))^2)^(1/2);

if norma<e

flag=1;

end;

if abs(f_old-fmin)<e

flag=1;

end;

end;

x_old=xk;

f_old=fmin;

end;

xk

fmin

k

Індивідуальне завдання:

1.Використовуючи розроблену програму (див. завдання 4), за методом бар’єрних функцій розв’язати наступні задачі математичного програмування з точністю до , починаючи з точки :

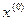2) ,

де ;

Результати:

Для е = 10^-4

x_old =

5.0065

4.0129

f_old =

-37.9998

k =

xk =

5.0065

4.0129

fmin =

-37.9998

Для е = 10^-8

x_old =

5.0004

4.0008

f_old =

-38.0000

k =

xk =

5.0004

4.0008

fmin =

-38.0000

Перевірка результатів за допомогою пакету Mathcad:

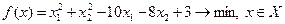
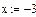
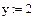
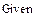
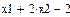
Дата добавления: 2015-08-21