
|
Читайте также: |
Альтернативные эвристические методы решения задач
Ниже раскрыто существо ряда математических методов, с помощью которых удается успешно решать плановые задачи в случае обнаружения в модели абсолютно доминирующего критерия оптимальности.
Иначе говоря, в тех исключительных случаях, когда не представляется возможным получить решение плановой или экономической задачи на основе непосредственно многокритериального подхода, предлагается использовать ряд достаточно эффективных эвристических (т.е. полученных в результате обобщения накопленного практического опыта) методов. Среди них наиболее перспективными и обеспечивающими получение в большинстве случаев вполне приемлемых с практической точки зрения (приближенно оптимальных) планов являются:
- метод «наибольшего подобия» [103];
- метод, базирующийся на использование в расчетах формулы линейного коэффициента корреляции [104];
- метод, получивший условное название косинуса многомерного пространства [105].
Общим для этих методов является то, что с помощью оригинальной системы расчетов в каждом из них, ищется степень сходства между структурой трудоемкостей участвующих в расчетах изделий (заготовок, деталей, сборочных единиц) и структурой подлежащих использованию в данном плановом периоде фондов времени основных групп рабочих мест (ОГРМ) или иных видов ресурсов. Приведем краткую характеристику перечисленным выше эвристическим методам и сопроводим их практическими иллюстрациями, отражающими существо необходимых расчетов.
Метод «наибольшего подобия». Сущность его состоит в том, что в план формируемого на данной стадии расчетов периода (например, месяца) в первую очередь включается такое изделие, структура трудоемкости которого имеет наибольшее сходство со структурой остающихся к использованию фондов времени основных групп рабочих мест.
Для четкого понимания существа данного метода приведем краткую постановку, экономико-математическую модель задачи распределения квартального плана и последовательность укрупненного вычислительного процесса.
Постановка задачи. Пусть необходимо распределить заданную на квартал номенклатуру (программу) изделий по месяцам с учетом обеспечения требования необходимой равномерности и полноты (сбалансированности) использования имеющихся фондов времени по основным группам рабочих мест. Под сбалансированностью загрузки основных групп рабочих мест подразумевается обеспечение такой их занятости работой, кото рая находится в пределах от 90 до 120% от величины первоначального подлежащего использованию фонда времени  .
.
Экономико-математическая модель задачи распределения
квартального плана по месяцам
 (
( (6.21)
(6.21)
 N
N 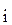 (
(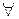 i) (6.22)
i) (6.22)
f(X) =  (
(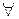 jk) (6.23)
jk) (6.23)
где
i - код изделия (i = 1,..., n);
j - код основной группы рабочих мест (j = 1,..., m);
N 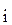 - программа выпуска i-го изделия на квартал, шт.;
- программа выпуска i-го изделия на квартал, шт.;
k - номер месяца квартала (k = 1,...,3);
х 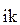 - количество изделий (партия изделий) i-го наименования,
- количество изделий (партия изделий) i-го наименования,
включенных в план k-го месяца данного квартала, шт.; 
t  - трудоемкость i-го изделия на j-ой ОГРМ, ч;
- трудоемкость i-го изделия на j-ой ОГРМ, ч;
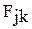 - подлежащий использованию фонд времени по j-ой ОГРМ в
- подлежащий использованию фонд времени по j-ой ОГРМ в
k - ом месяце квартала, ч; 
В выражении экономико-математической модели (6.21) сформулировано требование, предусматривающее обеспечение необходимой сбалансированности загрузки каждой ОГРМ в любом месяце квартала.
Уравнение (6.22) предусматривает безусловный выпуск всех участвующих в расчетах изделий на протяжении трех месяцев квартала.
Целевая функция (формализованная форма изображения критерия оптимальности) задачи (6.23) заключается в обеспечении необходимого уровня сбалансированности посредством минимизации относительного отклонения от равномерности загрузки каждой ОГРМ в любом месяце квартала.
Укрупненный алгоритм решения задачи распределения квартального плана по месяцам согласно методу «наибольшего подобия» включает следующие основные процедуры.
1. Формируется номер месяца, по которому предстоит формирование плана:
k:= 0; k:= k + 1, k = 1,…,3.
2. Определяются соотношения столбцов матрицы исходного числового материала. Для этого значения трудоемкости изделий по j - ой ОГРМ, включая подлежащие использованию фонды времени данного 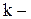 го месяца, делим на соответствующие значения трудоемкостей первого столбца (j = 1).
го месяца, делим на соответствующие значения трудоемкостей первого столбца (j = 1).
3. Вычисляется отклонение структуры трудоемкости каждого изделия от структуры остающихся к загрузке фондов времени в k - ом месяце (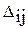 ). Это осуществляется путем вычитания из данных, полученных в
). Это осуществляется путем вычитания из данных, полученных в  ом столбце, соответствующих значений соотношения фондов времени различных ОГРМ.
ом столбце, соответствующих значений соотношения фондов времени различных ОГРМ.
4. Полученные отклонения (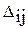 ) по
) по  ой ОГРМ суммируются по абсолютной величине для
ой ОГРМ суммируются по абсолютной величине для  -го изделия:
-го изделия:

где 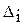 - суммарное отклонение i- го изделия от соотношения остающихся к использованию фондов времени в
- суммарное отклонение i- го изделия от соотношения остающихся к использованию фондов времени в 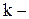 ом месяце.
ом месяце.
5. Выбирается изделие, у которого суммарное отклонение является наименьшим (min 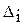 ). Это изделие имеет наибольший приоритет. Поэтому оно включается в план формируемого месяца.
). Это изделие имеет наибольший приоритет. Поэтому оно включается в план формируемого месяца.
6. Определяется коэффициент загрузки по каждой ОГРМ как отношение суммарной трудоемкости включенных в план формируемого k - го месяца изделий на данной стадии расчетов к первоначальной величине используемого фонда времени по данному месяцу (К 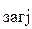 ).
).
Если 0,9  К
К  1,2, то рассматриваемое изделие включается в план формируемого месяца. Из дальнейших расчетов оно исключается. При этом корректируются остающиеся к использованию фонды времени по каждой ОГРМ на величину трудоемкости изделия:
1,2, то рассматриваемое изделие включается в план формируемого месяца. Из дальнейших расчетов оно исключается. При этом корректируются остающиеся к использованию фонды времени по каждой ОГРМ на величину трудоемкости изделия:
 ,
, 
где
х  - количество изделий i-го наименования, включенных в план
- количество изделий i-го наименования, включенных в план
формируемого 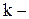 го месяца.
го месяца.
В противном случае, если изделие не обеспечивает соблюдение условия допустимой величины равномерности и полноты загрузки ОГРМ  , то оно помещается на временное хранение в нерабочее множество.
, то оно помещается на временное хранение в нерабочее множество.
Если окажется невозможно включить в план формируемого месяца ни одного из оставшихся изделий претендентов, то следует переход к п. 1. Иначе говоря, приступают к формированию плана следующего по порядку месяца. Далее процесс вычислений повторяется в том же порядке до тех пор, пока не наступит очередь формирования плана третьего месяца.
7. План третьего месяца определяется как разность между всей квартальной номенклатурой изделий и составом изделий, включенных в планы первого и второго месяцев.
Проиллюстрируем порядок расчетов по приведенному алгоритму на условном числовом примере. Пусть известны исходные данные, приведенные в табл. 16.
Таблица 16
Матрица числового материала по задаче распределение квартального
плана по месяцам
| Код Изделия (i) | Программа выпуска изделий на квартал, шт.
(N 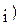
| Затраты необходимого времени на изготовление i-го изделия на j-ой ОГРМ, ч (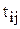 ) )
| ||
| j=1 | j=2 | j=3 | ||

| k=1 | |||
| k=2 | ||||
| k=3 |
Практический пример расчетов.
1. Формируется номер месяца, по которому предстоит формирование плана выпуска изделий: k:= 0 + 1 = 1.
2. Определяются соотношения столбцов матрицы исходного числового материала. Результаты расчетов приведены в табл. 17.
Таблица 17
Соотношения столбцов матрицы числового материала
| Код Изделия | Соотношения столбцов | ||
| 21:21=1 | 42:21=2,0 | 65:21=3,1 | |
| 73:73=1 | 52:73=0,71 | 208:73=2,85 | |
| 30:30=1 | 64:30=2,13 | 93:30=3,1 | |
| 147:147=1 | 115:147=0,78 | 365:147=2,48 | |
| 68:68=1 | 41:68=0,6 | 160:68=2,35 | |
| 121:121=1 | 93:121=0,77 | 309:121=2,55 | |

| 49:49=1 | 101:49=2,06 | 152:49=3,1 |
3. Вычисляется отклонение структуры трудоемкости изделия от структуры остающихся к загрузке фондов времени по ОГРМ в k-ом месяце (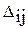 ). Результаты расчетов приведены ниже.
). Результаты расчетов приведены ниже.
| Код изделия | Результаты расчетов(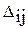 ) )
| (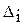 ) )
| ||
| 1-1= 0 |  2-2,06 2-2,06  = 0,06 = 0,06
| 3,1-3,1 = 0 | 0,06 | |
| 1-1= 0 |  0,71-2,06 0,71-2,06  = 1,35 = 1,35
|  2,85-3,1 2,85-3,1  = 0,25 = 0,25
| 1,6 | |
| 1-1= 0 | 2,13-2,06 = 0,07 | 3,1-3,1 = 0 | 0,07 | |
| 1-1= 0 |  0,78-2,06 0,78-2,06  = 1,28 = 1,28
|  2,48-3,1 2,48-3,1  = 0,62 = 0,62
| 1,9 | |
| 1-1= 0 |  0,6-2,06 0,6-2,06  = 1,46 = 1,46
|  2,35-3,1 2,35-3,1  = 0,75 = 0,75
| 2,21 | |
| 1-1= 0 |  0,77-2,06 0,77-2,06  = 1,29 = 1,29
|  2,55-3,1 2,55-3,1  = 0,55 = 0,55
| 1,84 |
Из приведенных выше расчетов видно, что по первому изделию имеет место наибольшее сходство структуры трудоемкости со структурой подлежащих использования фондов времени ОГРМ. Следовательно, оно и должно быть включено в план формируемого первого месяца. В дальнейших расчетах первое изделие не участвует.
4. Корректирование остающихся к использованию фондов времени по ОГРМ в результате включения первого изделия в план первого месяца:
| Код основных групп рабочих мест | ||
| Остающиеся к использованию фонды времени | ||
| 49 - 21 = 28 | 101 - 42 = 59 | 152 - 65 = 87 |
5. Матрица исходного числового материала принимает новый вид:
| Код Изделия (i) | Программа выпуска изделий на квартал, шт.
(N 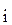 ) )
| Затраты необходимого времени на изготовление i-го изделия на j-ой ОГРМ, ч (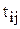 ) )
| ||
| j=1 | j=2 | j=3 | ||
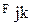
|  =1 =1
|
6. Вновь определяются соотношения столбцов матрицы исходного числового материала. Результаты расчетов приведены в табл. 18.
Таблица 18
Соотношения столбцов матрицы числового материала
| Код Изделия | Соотношения столбцов | ||
| 73:73 = 1 | 52:73 = 0,71 | 208:73 = 2,85 | |
| 30:30 = 1 | 64:30 = 2,13 | 93:30 = 3,1 | |
| 147:147 = 1 | 115:147 = 0,78 | 365:147 = 2,48 | |
| 68:68 = 1 | 41:68 = 0,6 | 160:68 = 2,35 | |
| 121:121 = 1 | 93:121 = 0,77 | 309:121 = 2,55 | |

| 28:28 = 1 | 59:28 = 2,11 | 87:28 = 3,11 |
7. Повторяется вычисление абсолютных отклонений структуры трудоемкости изделия от структуры остающихся к загрузке фондов времени ОГРМ в к-ом месяце (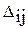 ). Результаты расчетов представлены в табл. 19.
). Результаты расчетов представлены в табл. 19.
Таблица 19
Результаты расчетов абсолютных отклонений структуры
трудоемкости изделий от структуры фондов времени
| Код Изделия | Результаты расчетов(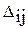 ) )
| (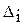 ) )
| ||
| 1-1= 0 |  0,71-2,11 0,71-2,11  = 1,4 = 1,4
|  2,85-3,11 2,85-3,11  = 0,26 = 0,26
| 1,66 | |
| 1-1= 0 | 2,13-2,11 = 0,02 | 3,1-3,11 = 0,01 | 0,03 | |
| 1-1= 0 |  0,78-2,11 0,78-2,11  = 1,33 = 1,33
|  2,48-3,11 2,48-3,11  = 0,63 = 0,63
| 1,96 | |
| 1-1= 0 |  0,6-2,11 0,6-2,11  = 1,51 = 1,51
|  2,35-3,11 2,35-3,11  = 0,76 = 0,76
| 2,27 | |
| 1-1= 0 |  0,77-2,11 0,77-2,11  = 1,34 = 1,34
|  2,55-3,11 2,55-3,11  = 0,56 = 0,56
| 1,9 |
8. Из приведенных в табл. 19 расчетов видно, что по третьему изделию имеет место наибольшее сходство структуры трудоемкости со структурой подлежащих использования ОГРМ. Следовательно, оно и должно быть включено в план формируемого первого месяца. В дальнейших расчетах третье изделие не участвует.
9. Корректирование остающихся к использованию фондов времени по ОГРМ в результате включения третьего изделия в план первого месяца:
| Код основных групп рабочих мест | ||
| Остающиеся к использованию фонды времени ОГРМ | ||
| 28 - 30 = -2 | 59 - 64 = -5 | 87 - 93 = -6 |
Как видим, фонды времени по всем ОГРМ исчерпаны.
10. Рассчитаем коэффициенты загрузки по каждой ОГРМ:
| Код основных групп рабочих мест | ||
| Коэффициенты загрузки по ОГРМ | ||
| (21+30): 49 = 1,04 | (42+64): 101 = 1,055 | (65+93): 152 = 1,04 |
Полученные коэффициенты загрузки ОГРМ по плану первого месяца находятся в пределах допустимых значений (не меньше 90% и не больше 120%). Переходим к формированию плана второго месяца квартала.
11. Самостоятельно сформировать план второго и третьего месяца.
Результаты окончательных расчетов по методу «наибольшего подобия» поместить в табл. 23.
Таблица 23
План распределения изделий квартальной программы по месяцам, полученный при использовании «метода наибольшего подобия»
| Первый месяц | Второй месяц | Третий месяц | ||||||
| Включенные в план коды изделий | ||||||||
| 1 и 3 | ||||||||
| Коэффициенты загрузки ОГРМ | ||||||||
j=1 
| j=2 | j=3 |  j=1 j=1
| j=2 | j=3 | j=1 | j=2 | j=3 |
| 1,04 | 1,05 | 1,04 |
Дата добавления: 2015-08-21; просмотров: 42 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| коэффициента корреляции | | | Завдання |