коэффициента корреляции

Для определения степени сходства между структурой трудоемкости участвующих в расчетах изделий и структурой подлежащих использованию фондов времени ОГРМ предлагается линейный коэффициент корреляции (r(t_ij; F_jk)):

r(

При этом последовательность вычислительного процесса остается примерно такой же, что и при использовании метода «наибольшего подобия».

Выполнение расчетов по данному методу записать на лист 2 Microsoft Excel.

Система расчетом в этом случае включает следующие основные этапы.

1. Формируется номер месяца, по которому необходимо сформировать план выпуска изделий. Начинают построение плана с первого месяца.

2. Рассчитываются по изделиям линейные коэффициенты корреляции, которые отражают степень сходства между структурой их трудоемкости и подлежащими использованию фондами времени по ОГРМ. Применительно к первому изделию коэффициент корреляции после подстановки в него соответствующих цифровых данных будет иметь такой вид:

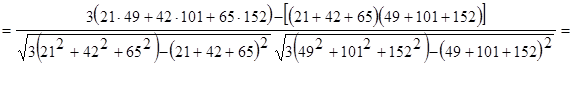
= 0,9996

Результаты расчетов численных значений линейных коэффициентов корреляции по всем изделиям сведены в табл. 2.1.

Таблица 2.1

Численные значения линейных коэффициентов корреляции

Код изделия	Коэффициент корреляции
	0,9996

На основании полученных данных табл.1 определить изделие которое имеет наибольшее сходство между структурой трудоемкости и подлежащими загрузке ОГРМ в первом месяце квартала (изделие у которого коэффициент корреляции МАКСИМАЛЕН).Оно и подлежит первоочередному включению в план формируемого месяца.

3. Корректирование остающихся к использованию фондов времени по ОГРМ в результате включения этого изделия в план первого месяца (табл. 2.2).

Таблица 2.2

Результаты корректировки фондов времени по ОГРМ

Код основных групп рабочих мест
Остающиеся к использованию фонды времени, ч
49 - =	101 - =	152 - =

Из дальнейших расчетов первое изделие выбывает.

4. Для изменившихся условий повторяется процедура, связанная с определением численных значений линейных коэффициентов корреляции. Результаты этих вычислений приведены в табл. 2.3.

Таблица 2.3

Численные значения линейных коэффициентов корреляции

Код изделия	Коэффициент корреляции

По результатам проведенных вычислений включаем в план первого месяца изделие с МАКСИМАЛЬНЫМ коэффициентом корреляции.

5. Корректирование остающихся к использованию фондов времени по ОГРМ в результате включения i-го изделия в план 1-го месяца (табл. 2.4).

Таблица 2.4

Результаты корректировки фондов времени по ОГРМ

Код основных групп рабочих мест
Остающиеся к использованию фонды времени

6. Рассчитаем коэффициенты загрузки по каждой ОГРМ для сформированного плана первого месяца (табл. 2.5).

Таблица 2.5

Результаты расчетов коэффициентов загрузки ОГРМ

Код основных групп рабочих мест
Коэффициенты загрузки по ОГРМ
(+): 49 =	(+): 101 =	(+): 152 =

Проверяем находятся ли полученные коэффициенты загрузки ОГРМ по плану первого месяца находятся в пределах допустимых значений. Если да, то переходим к формированию плана второго месяца квартала.

7. Формируем план второго и третьего месяца.

Сводим результаты расчетов по методу, основу которого составляет формула линейного коэффициента корреляции, в табл.2.1.1.

Таблица 2.1.1

План распределения изделий квартальной программы по месяцам, полученный на основе применения линейного коэффициента корреляции

Первый месяц	Второй месяц	Третий месяц
Включенные в план коды изделий
Коэффициенты загрузки ОГРМ
j=1	j=2	j=3	j=1	j=2	j=3	j=1	j=2	j=3

Метод, называемый косинусом многомерного пространства. Ниже описан метод, который хотя и не приводит к оптимальному плану, но все же позволяет получать вполне практически приемлемые для руководящих менеджеров решения. Этот метод условно был назван методом косинуса многомерного пространства.

Формула для m групп рабочих мест (для m -мерного пространства) имеет вид:

cos .

Все расчеты по данному методу необходимо поместить в Excel на лист 3.

Для иллюстрации решения задачи распределения квартального плана по месяцам воспользуемся теми же исходными данными, которые были приведены на листе 1 Microsoft Excel в табл. 1. 1.

Последовательность расчетов остается прежней.

1. Формируется номер месяца, по которому необходимо сформировать план выпуска изделий. Начинают построение плана с первого месяца.

2. Рассчитываются числовые значения Cos²j по всем изделиям. Для иллюстрации приведем расчет по первому изделию:

Cos²j =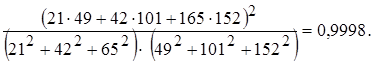

Численные значения Cos²j по всем конкурирующим изделиям сведены в табл. 3.1.

Таблица 3.1

Численные значения Cos²j по изделиям, претендующим к включению в план первого месяца

Код изделия	Cos^2j
	0,9998

Включаем в первую очередь в план 1-го месяца изделие с наибольшим значением Cos²j.

3. Корректирование остающихся к использованию фондов времени по ОГРМ в результате включения i-го изделия в план первого месяца (см. табл. 15). Из дальнейших расчетов i-е изделие выбывает.

4. Для изменившихся условий повторяется процедура, связанная с определением численных значений Cos²j. Результаты этих вычислений приведены в табл. 3.2.

Таблица 3.2

Численные значения Cos²j по оставшимся нераспределенным

изделиям

Код изделия	Cos^2j

Включаем в план 1-го месяца изделие с наибольшим значением Cos²j.

5. Корректирование остающихся к использованию фондов времени по ОГРМ (табл. 3.3).

Таблица 3.3

Результаты корректировки фондов времени по ОГРМ

Код основных групп рабочих мест
Остающиеся к использованию фонды времени

6. Рассчитаем коэффициенты загрузки по каждой ОГРМ.

Если полученные коэффициенты загрузки ОГРМ по плану первого месяца находятся в пределах допустимых значений, то переходим к формированию плана второго месяца квартала.

7. Формируем план 2 и 3 месяца.

В сводном виде результаты решения задачи распределения выпуска изделий по месяцам квартала приводятся в табл. 3.1.1.

Таблица 3.1.1

Результаты распределения квартального плана по месяцам по методу, основывающемуся на применении Cos²j

Номер месяца	Коды включенных изделий	Коэффициенты загрузки ОГРМ
j=1	j=2	j=3

Для определения наиболее предпочтительного из трех рассмотренных выше методов приведем для сравнения значения целевых функций, соответствующих полученным результатам решения задачи распределения квартального плана по месяцам на одном и том же числовом материале (табл. 4.1).

Таблица 4.1

Значения целевых функций, соответствующих вариантам решения

задачи с помощью трех различных методов

Но-мер ме-сяца	Альтернативные методы
«наибольшего подо- бия»	с использованием коэффициента корреляции	с использованием косинуса многомер- ного пространства
числовые значения целевой функции, представляющих собой относительные отклонения от равномерности загрузки ОГРМ
j=1	j=2	j=3	j=1	j=2	j=3	j=1	j=2	j=3
k=1
k=2
k=3

Из приведенной в табл.4.1 расчетной информации можно сделать следующие выводы.

1. Варианты решения задачи распределения квартального плана по месяцам, полученные с помощью методов «наибольшего подобия» и линейного коэффициента корреляции, удовлетворяют всем требованиям экономико-математической модели. Следовательно, они могут быть признаны оптимальными. Решение, полученное на основании применения метода, условно названного косинусом многомерного пространства, не удовлетворяет требованию равномерности загрузки ОГРМ. Поэтому его нельзя признать приемлемым.

Параметрическая оценка качества полученных вариантов планов предлагается осуществлять с помощью следующих показателей.

1. Суммарное абсолютное отклонение от равномерности загрузки ОГРМ по плановому периоду

D = ,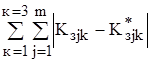

где

K - коэффициент загрузки j-ой ОГРМ в k-м месяце квартала

(k=1,…,3);

К - так называемый эталонный коэффициент загрузки ОГРМ по

j-ой ОГРМ в k-ом месяце, равный 1.

2. Среднеквадратическое отклонение от равномерности загрузки ОГРМ.

s = .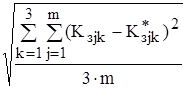

3. Вариационный размах:

R (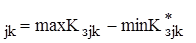

Результаты расчетов перечисленных выше показателей по трем вариантам распределения квартального план по месяцам с помощью трех альтернативных методов cпоместить в табл. 4.2.

Таблица 4.2

Численные оценки значений показателей, используемых для оценки

уровня качества полученных трех различных вариантов планов

распределения квартального плана по месяцам

Показатель	Вариант распределения квартального плана по месяцам, полученный с помощью
метода «наибольшего подобия»	линейного коэффициента корреляции	Косинуса многомерного пространства
Суммарное абсолютное отклонение от равномерности загрузки
Среднеквадратическое отклонение
Вариационный размах

На основании табл. 4.2 определяем наилучший вариант плана (тот у которого полученные показатели МИНИМАЛЬНЫ).

По результатам выполнения лабораторной работы сформировать отчет, показывающий последовательность проведенных вычислений по каждому методу.

Дата добавления: 2015-08-21