Алгоритм метода ветвей и границ

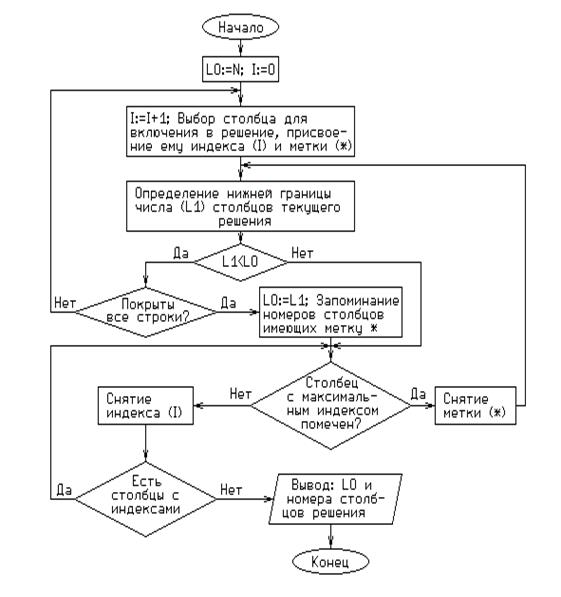
Исходными данными для применения алгоритма является матрица, представляющая собой приближенное решение задачи о наименьшем покрытии с вычеркнутыми столбцами, включенными в оптимальное решение, и строками, которые они покрывают.

Обозначения:

N-число столбцов;

L0-число столбцов для включения в решение задачи о покрытии;

L1-нижняя граница (наименьшее число покрывающих столбцов).

Мощность столбца – число единиц в нем, расположенных в непокрытых строках.

Определение величины L1.

Оценка нижней границы количества покрывающих столбцов рассчитывается по формуле

L1=СТ^*+СТ, где СТ^*-число столбцов со звездочкой;

СТ-минимальное число покрывающих столбцов, не имеющих индекса, суммарная мощность которых больше или равна числу непокрытых строк.

Если суммарная мощность меньше числа непокрытых строк, то L1=N.

В табл.1 представлена исходная матрица покрытий.

Таблица 1

Для нахождения приближенного решения столбец с наибольшей мощностью (j=4) помечаем знаком (*), а соответствующие покрываемые строки – знаком (+). Для покрытия непокрытых строк необходим еще один столбец (j=3), его также помечаем знаком (*), а покрываемые им строки – знаком (+). Так как все строки перекрыты, следовательно, приближенное решение найдено. Приближенным решением являются столбцы (J=3, J=4).

Рассмотрим теперь нахождение оптимального решения по приведенному выше алгоритму.

2) Так как размер матрицы равен 8,то L0=N=8, I=0;

3) i=1; столбец (j=4)с максимальной мощностью помечаем знаком * и ”1”, а покрываемые им строки – знаком (+);

4) Так как звездочкой помечен один столбец, а для покрытия всех элементов нужен еще один столбец, то L1=1+1=2;

5) L1<8, да;

6) покрыты не все строки;

3) I=2, столбец (j=3) помечаем знаком (*) и ”2”, а перекрываемые им строки – знаком (+);

4) Так как звездочкой помечено два столбца, все элементы покрыты, то L1=2+0=2;

5) L1<8, да;

6) покрыты все строки;

7) L0=2 {j=3; j=4};

8) столбец (j=3) с максимальным индексом помечен знаком (*);

9) снимаем знаки (*) и (+) со столбца j=3;

4) Так как звездочкой помечен один столбец, для покрытия всех элементов нужен один столбец, то L1=1+1=2;

5) 2<2, нет;

8) столбец с максимальным индексом не помечен знаком (*);

10) снимаем индекс ”2”;

11) есть столбцы с индексами;

8) столбец с максимальным индексом (j=4) помечен знаком (*);

9) снимаем метки (*) и (+) со столбца №4;

4) Так как ни один столбец не помечен звездочкой, для покрытия всех строк требуется два столбца, поэтому L1=0+2=2;

5) 2<2, нет;

8) столбец с максимальным индексом (j=4) не помечен знаком (*);

10) снимаем индекс ”1”;

11) столбцов с индексами нет;

12) Вывод: L0=2, j=3, j=4 – решения.

Дата добавления: 2015-08-21