Решение задачи о кратчайшем пути в графе на основе ЛП

Модель ЛП для задачи о кратчайшем пути строится следующим образом: пусть Х_ij – наличие пути из i-ой вершины в j–ю. Если Х_ij=1, то путь есть, если Х_ij=0, то пути нет. D_ij-стоимость перемещения из i-ой вершины в j–ю (расстояние). Тогда движение по всем путям должно быть минимально, т.е.

N N

Z= ∑ ∑ d_ijX_ij→min.

I=1 j=1

Из исходного пункта в любой другой везем продукт 1, а сумма всех входящих поездок равна сумме всех выходящих. Для конечной вершины из всех вершин должна придти 1.

Исходный граф имеет следующий вид

Х₂ Система ограничений

Х₁ - Х₂=0

Х₁ d=7 Х₂ + Х₃=1

К Х₄ – Х₃=0

D=5 Х₁ + Х₄=1

Х₃

Н d=3 Целевая функция

F=5Х₁+7Х₂+3Х₃+10Х₄

Х₄ d=10 Х_j≥0, Х_i-целочис-

ленные

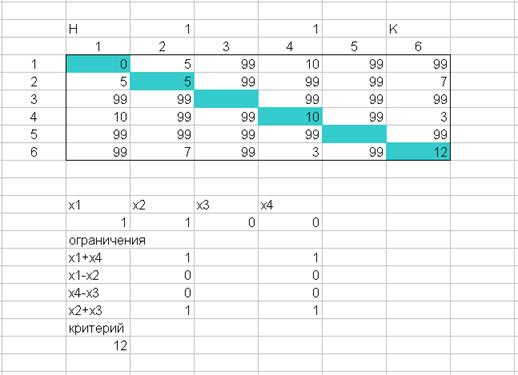
Тогда в программе Excel получим следующее решение данной задачи, которое полностью совпадает с решением задачи методом Форда. Критерием будет являться целевая функция.

Дата добавления: 2015-08-21