Получение уравнения гиперплоскости, проходящей через n заданных точек.

y

А

• Надо найти уравнение АВ.

В

(0;-1) 0 х

Рисунок 4.

В общем виде:

ay+bx+c=0

a*1+b*0+c=0 (A)

a*0+b*(-1)+c=0 (B)

Имеем 2 уравнения с 3 неизвестными.

Пусть а=1

у+ bх+с=0

х=const-нельзя провести.

Пусть b=1

ау+х+с=0

у=const-нельзя провести.

Пусть с=1

ау+bх+1=0

у=кх-нельзя провести.

Вводятся дополнительные координаты и дополнительные точки.

у

А (1,0,0)

В

(0,-1,0) х

•

С(-1,0,1)

z

Значение одной из координат дополнительной точки (в данном случае у, не считая координаты по введенной оси z) меньше минимального значения или больше максимального значения соответствующей координаты множества граничных точек. Проводим плоскость через эти точки.

у

А (1,0,0)

В

(0,-1,0) х

•

С(-1,0,1)

z

Уравнение плоскости имеет вид:

ау+bх+γz+с=0

В этом уравнении составим координаты 1-й,2-й и 3-й точек.

а*1+b*0+γ*0+с=0

а*0+b*(-1)+γ*0+с=0

а*(-1)+b*0+γ*1+с=0

Получили 3 уравнения с 4 неизвестными, но в этой системе уравнений можно задаваться γ, равной постоянной величине 1 и решить данную систему уравнений.

Пусть γ=1, тогда

1)а=-с

2)b=с

3)2с+1=0 с=-0,5

0,5у-0,5х-0,5=0.

Упорядоченное множество -множество, у которого каждый элемент занимает определенное место.

ПРИМЕР: дано множество {a,I,j,k,l,m}

Индексы

a-оценка

i-номер предмета

j-номер преподавателя

k-время

l-номер группы

m-номер студента

Многомерная матрица - упорядоченная совокупность многоиндексных элементов.

i⁺-столбцовый индекс

i^--строчный индекс

A(p,q)-обозначение матрицы в общем виде.

p-число столбцовых индексов.

q -число строчных индексов.

ПРИМЕР:

А(1;0)={ }=

i=1	a1
i=2	a2

Общее индексное

представление представле-

матрицы ние матрицы
табличное

Правило помечивания для индексного представления матрицы A(p,q).

A(p,q)={a_i,j,k,..}, число индексов равно p+q. Крайний справа индекс всегда строчный, если таковой имеется. Далее индексы справа налево чередуются по типу до тех пор, пока не кончаются индексы одного типа. Далее индексы идут без чередования. Индекс слева старше, чем индекс справа. Индекс слева дает более крупный блок.

ПРИМЕР:

	j=1	j=2
i=1	a11	a12
i=2	a21	a22

A(1,1)={ }=

	i=1	i=2
K=1	K=2	K=1	K=2
j=1	a111	a112	a211	a212
j=2	a121	a122	a221	a222

A(1,2)={ }=

	n=1	n=2
l=1	m=1	b111	b112
m=2	b121	b122
l=2	m=1	b211	b212
m=2	b221	b222

B(2,1)={ }=

Операции над многомерными матрицами.

1. Умножение многомерной матрицы на скаляр.

2. Сложение многомерных матриц.

A(p,q)+B(p,q)=C(p,q)

Складывать можно матрицы только одинаковой структуры.

3. Транспонирование многомерных матриц.

Индексы строчных переводятся в столбцовые, а столбцовые в строчные. Далее индексы расставляются по правилу помечивания. Полученная матрица определяет структуру матрицы, а значения ее элементов определяются по исходной матрице при одноименных значениях индексов.

	j=1	j=2
i=1	a11	a12
i=2	a21	a22

A(1,1)={ }=

	i=1	i=2
j=1	a^T11	a^T12
j=2	a^T21	a^T22

(A(1,1))^Т={ }=

	i=1	i=2
j=1	a11	a12
j=2	a21	a22

=

4. Свернутое произведение многомерных матриц.

А(1,2)*В(2,1)

Свертка -суммирование произведения элементов по определенным индексам. Свертываться могут строчные индексы первого сомножителя со столбцовыми индексами второго сомножителя. Свертка проходит в естественном порядке: 1-й строчный слева с 1-м столбцовым слева; 2-й строчный со 2-м столбцовым. Несвернутые строчные индексы 1-го сомножителя ставятся всей группой после строчных индексов 2-го сомножителя. Свернутые индексы исчезают из результата. Полученная матрица определяет структуру матрицы, а значения ее элементов определяются сверткой по соответствующим индексам.

А(1,2)*В(2,1)= здесь индексы l и m приравниваются к индексам i и k.

	n=1	n=2
j=1	c11	c12
j=2	c21	c22

ПРИМЕР:

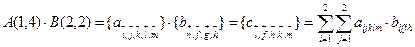
5. Кронекеровское произведение матриц

А В

Табличное представление

А(0,1)={1,2,3}

B(0,1)={4,5,6}

На место каждого элемента 1-го сомножителя ставиться произведение этого элемента на весь 2-й сомножитель.

C(0,2)={4,5,6,8,10,12,12,15,18}

Индексное представление

1)индексы не свертываются.

2)индексы 1-го сомножителя предшествуют индексам 2-го сомножителя.

Далее индексы рассматриваются по правилу помечивания. Полученная матрица определяет структуру, а значение ее элементов при одноименных значениях индексов.

А(0,1)={ }

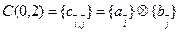
i=1	i=2	i=3
j=1	j=2	j=3	j=1	j=2	j=3	j=1	j=2	j=3
C11	C12	C13	C21	C22	C23	C31	C32	C33

{C_ij}=
C₂₁=a₂*b₁=8

ПРИМЕР:

6. Векторизация матриц.

A(p,q) 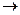A⁺(p+q,0)

A(p,q)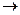

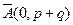
Представляется либо в виде одной строки, либо в виде одного столбца.

а) столбцовая векторизация

Строчные индексы переводятся в столбцовые и всей группой ставятся после непереведенных столбцовых индексов. Полученная матрица определяет структуру, а значение ее элементов определяется по исходной матрице при одноименных значениях индексов.

	j=1	j=2
i=1	a11	a12
i=2	a21	a22

A(1,1)={ }=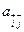

i=1	j=1	a^+11
j=2	a^+12
i=2	j=1	a^+21
j=2	a^+22

A⁺(2,0)={ }=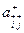
()

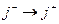i=1	j=1	a11
j=2	a12
i=2	j=1	a21
j=2	a22

=

б) строчная векторизация

А(1,1)={ }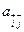

При строчной векторизации столбцовые индексы переводятся в строчные и всей группой ставятся после непереведенных строчных индексов. Полученная матрица определяет структуру матрицы, а значение ее элементов определяется по исходной матрице.

j=1	j=2
i=1	i=2	i=1	i=2

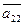
Получим значения матрицы

j=1	j=2
i=1	i=2	i=1	i=2
a11	a21	a12	a22

(i⁺ i^-)

7. Девекторизация

а) столбцовая Д-векторизация

При столбцовой Д-векторизации индексы столбцовые, ранее переведенные из строчных в столбцовые вновь переводятся в строчные и всей группой ставятся впереди (с левой стороны) от непереведенных столбцовых индексов. Далее индексы расставляются по правилу помечивания.

Имеем: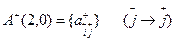

i=1	j=1	a11
j=2	a12
i=2	j=1	a21
j=2	a22

A(2,0)=
Переводим индекс столбцовый в строчный

	j=1	j=2
i=1	a11	a12
i=2	a21	a22

А(1,1)={ }=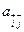

б) строчная Д-векторизация

При строчной Д-векторизации строчные индексы, ранее переведенные из столбцовых в строчные вновь переводится в столбцовые и ставятся впереди (слева) непереведенных строчных индексов. Далее расставляются по правилу помечивания.

	j=1	j=2
i=1	a11	a12
i=2	a21	a22

A(1,1)={ }=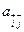

8. Обращение многомерной матрицы

Обратная матрица строится на основе обращения ее табличного представления. Имеем многомерную матрицу и в ней убираем все перегородки и оставляем только строки и столбцы.

Д-определитель матрицы

B_ij-определитель матрицы, полученный из исходной матрицы А путем вычеркивания j-й строки и i-го столбца.

	j=1	j=2
i=1
i=2

Д=3-8=-5

Структура обратной матрицы определяется также, как и при транспонировании многомерной матрицы.

	i=1	i=2
j=1	-3/5	2/5
j=2	4/5	-1/5

	i=1	i=2
	к=1	к=2	к=3	к=1	к=2	к=3
j=1
j=2
j=3
j=4
j=5
j=6

1/2
	1/2
		1/2

	j=1	j=2	j=3	j=4	j=5	j=6
i=1	k=1	1/2
k=2		1/2
k=3			1/2
i=2	k=1
k=2
k=3

A(1,2)*A^-1(2,1)=E аналогично A^-1(2,1)* A(1,2)=Е.

Это свойство используется при решении линейных алгебраических уравнений.

Дата добавления: 2015-08-21