Динаміка конкурентоспроможності

До цих пір величини, що входять у наведені вище формули, вважалися постійними, проте на практиці вони не є такими. У першу чергу, змінними є L₀, L. Їх змінність обумовлена як технічними, так і економічними причинами, в першу чергу - інфляцією, під впливом якої наведені витрати зростають.

Припустимо, що вплив інфляції враховується таким чином

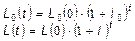, (18)

де: L₀(0) – витрати на ЖЦ «базового виробу» в «нульовий» рік, тобто в рік виконання розрахунку; I₀ – коефіцієнт (норма) річної інфляції для базового виробу (передбачається, що базовий виріб – іноземного виробництва); L(0), I - ті ж величини для виробу, стосовно якого розраховується КС.

Тоді

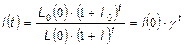(19)

Якщо припустити, що q = q(0)=const, l = l(t), то підставляючи (19) в (11), отримаємо

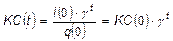, (20)

де .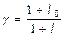

Якщо в «нульовий» рік величина КС(0) >1, то з (20) можна знайти тривалість періоду часу, в перебігу якого виріб залишатиметься конкурентоспроможним стосовно до базового. Очевидно, що гранична умова конкурентоспроможності

КС(t) = 1.

Тоді, підставляючи в ліву частину рівняння (20) значення КС(t)=1 і, логарифмуючи отримаємо:

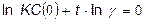
. (21)

Приклад 1.

Нехай КС(0) = 2, інфляція в «базовій» країні становить 2 % за рік, а в Україні – 10 % за рік. Тоді:

; ;

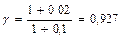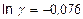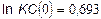
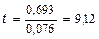років.

Відмітимо далі, що показник конкурентоспроможності може знижуватися у міру вдосконалення (підвищення показників якості) базового виробу. Якщо припустити, що зміна показника якості q відбувається аналогічно зміні l, то формулу (20) можна подати у вигляді

, (22)

де d>1 – коефіцієнт, який визначає відносне підвищення якості базового виробу.

Вважаючи, як і вище, що в (22) КС(t) = 1, і логарифмуючи можна отримати вираз для оцінки тривалості періоду збереження конкурентоспроможності, що враховує зміну обох чинників:

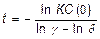(23)

Приклад 2.

Нехай виконуються умови прикладу 1. Величину d визначимо, припускаючи, що рівень якості наукоємкої продукції подвоюється кожні 8 - 10 років. Тоді 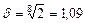або .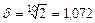

Величина t буде дорівнювати

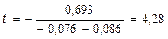або

роки.

Таким чином, в умовах діючої інфляції і з урахуванням темпів науково - технічного прогресу виріб, що має у момент початку проектування достатньо високу оцінку КС(0) =2, перестане бути конкурентоспроможним на світовому ринку всього через 4-5 років. Звідси випливає, що час виведення такого виробу на ринок повинен бути не більше 2-2,5 років з моменту початку проектування. Якщо в такий термін укластися неможливо, то в проект, що розробляється, треба закладати істотно великі значення КС(0). Так, при КС(0) =3 отримаємо

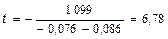або

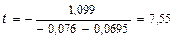роки.

На рис. 2 залежність t від КС(0) показана графічно. При необхідності за цим графіком можна визначити величину KC(0), відповідну заданому значенню t. Так, при t=10 років КС(0) =4,6 (штрихові стрілки).

Аналітичний вираз для КС(0) можна отримати з (23)

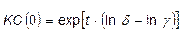(24)

Дата добавления: 2015-09-03