Вычисление стандартного отклонения

Обычно помимо среднего значения оценок мы хотим знать еще кое-что, а именно, какова несистематическая вариация оценок от пробы к пробе. Наиболее распрост­раненный способ измерения несистематической вариа­ции состоит в вычислении стандартного отклонения.

Для этого, вы определяете, насколько каждая оцен­ка (т. е. X) больше или меньше среднего (М_х). Затем вы возводите в квадрат каждую разность (X-М_х) и складываете их. Вслед за этим вы делите эту сумму на N число проб. Наконец, вы извлекаете квадратный корень из этого среднего.

Это вычисление представлено формулой с исполь­зование символа σ_х для обозначения стандартного отклонения:

(2.1)

90Эту формулу можно сократить, введя маленькое х для обозначения (X-М_х). Тогда формула выглядит так:

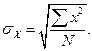(2.1A)

Давайте выпишем данные по условию А из приложения к главе I и одновременно произведем по ним вычисле­ния, указываемые формулой для σ_х

Проба	X	Мх	X - МX	x^2
или х
			+38	+1444
			—1	+1
			+24	+576
			—2	+4
			—5	+25
			—17	+289
			+30	+900
			—13	+169
			+15	+225
			+6	+36
			+12	+144
			+3	+9
			—11	+121
			—9	+81
			-30	+900
			—20	+400
			—22	+484
			Σ x^2	+5808

Поскольку

то

мс.

Дата добавления: 2015-09-03