Теоретическая часть

ВВЕДЕНИЕ

Повышение эффективности урока – важнейшая проблема, волнующая всех учителей. Снижение уровня знаний в значительной степени объясняется качеством урока: надежным стандартом, шаблоном, однообразием, формализмом, скукой. Педагоги ищут разные способы «оживления» урока, разнообразия форм объяснения и обратной связи, привлечения учащихся к активной работе.

Какие бы новации ни вводились, только на уроке, как сотни и тысячи лет назад, встречаются участники образовательного процесса: учитель и ученик. От того, какой будет эта встреча, зависит многое.

Современный урок – это урок, в результате которого открывается и создается что-то новое, собственный продукт творчества: открытие превращается в изобретение, изобретение – в проект, проект – в технологии реальной деятельности.

Целью работы является создание нестандартных игровых ситуаций на уроке, которые помогут активизировать познавательную деятельность учащихся, развить их творческую самостоятельность и тем самым повысить результативность урока.

Для реализации цели я поставила задачи:

· проанализировать психолого-педагогическую и методическую литературу по исследуемой проблеме;

· структурировать виды нестандартных игровых заданий, способствующих продуктивной деятельности учащихся;

· создать банк нестандартных игровых уроков по математике;

· развить у учащихся интерес к самообучению, творчеству, умение в нестандартной форме систематизировать материал, оригинально мыслить и самовыражаться.

В решении поставленных задач помогли статьи «Настаунiцкай газеты», научно-методического журнала «Матэматыка: праблемы выкладання», книги из серии «педагогическая мастерская» и другие предметные издания.

Теоретическая часть

Учиться играя.

Работа, связанная с личностно ориентированным обучением, стимулирует учителя к творчеству, поиску форм, методов, позволяющих развивать личность каждого учащегося.

Создать такие условия можно за счет наполнения предмета личностным содержанием, за счет гуманизации педагогических отношений. Вопрос в том, каким образом наполнить содержание личностным смыслом, является сложным вопросом, и существуют разные подходы к его реконструкции. Одним из таких подходов является привлечение дополнительной гуманитарной информации. Это позволяет выйти за традиционные рамки предмета в сферу человеческих отношений, нравственности, духовности, рассматривать учебный материал в контексте всей культуры и социальной практики человека. Выбирая форму организации урока, на котором будет рассматриваться дополнительный гуманитарный материал, учитель и ученик являются соавторами, собеседниками, совместно выбирают и ставят цели, темы урока. Кроме того каждый ученик имеет возможность выбрать вид деятельности на уроке – участие в исторических справках, демонстрация знаний и умений по теме, решение задач творческого характера. Тем самым востребуется личностная функция – рефлексия притязаний, самооценивание. И такая форма урока позволяет поставить в ситуацию успеха большинство учащихся. Итоговый результат – приобретение личностного опыта. Ведь личность может быть там, где нет принуждения, а есть требовательность, где успех достигается благодаря увлеченности, рожденной интересным преподаванием, и приложению усилий для преодоления трудностей. Использование дополнительного гуманитарного материала позволяет не только активизировать познавательную деятельность учащихся, но и сформировать у них свое отношение к истине, понимание относительности всякого знания, скромность в оценке собственных достижений. Игровая же деятельность на уроке позволяет создать условия для развития инициативы и творчества, для становления личностных функций – культуры нравственного выбора, рефлексивных механизмов поведения, реализации своего «я», для создания атмосферы сотрудничества.

Каждый учитель понимает, что нынешний урок очень сильно отличается от урока 10 лет назад. Ведь нынешний урок – это урок свободный, порожденный стремлением гуманизировать деятельность, признать человека как наивысшую ценность, предоставить ему максимум свободы для индивидуального развития, утвердить в повседневной реальности ценности достойной жизни; это урок свободный от страха. Ведь нынешний урок – это работа души, и тем усерднее эта работа, чем уважительнее отношение ребенка к самому себе, а также учителя к своей собственной личности. Гордый человек, беспокоящийся за собственное развитие и уровень образования, каждую учебную минуту посвятит работе.

Кроме этого, залогом урока является использование занимательности, наглядности, ТСО, личностно ориентированных ситуаций: выбора, успеха, неуспеха.

Использование игры в рамках учебно-воспитательного процесса – явление не новое. В игре воссоздается предметное и социальное содержание деятельности, моделирование систем отношений, адекватных условий формирования личности.

Игра не заменяет полностью традиционные формы и методы обучения; она рационально их дополняет, позволяя более эффективно достигать поставленной цели и задачи конкретного занятия и всего учебного процесса. В то же время игра повышает интерес обучающихся к учебным занятиям, стимулирует рост познавательной деятельности. Игра улучшает отношения между ее участниками и педагогами, так как игровые взаимодействия предусматривают неформальное общение и позволяют раскрыть и тем и другим свои личностные качества, лучшие стороны своего характера; она повышает самооценку участников игры, так как у них появляется возможность от слов перейти к конкретному делу и проверить свои способности. Игра изменяет отношение ее участников к окружающей действительности, снимает страх перед неизвестностью. Она одновременно ставит ученика в несколько позиций. Личность находится одновременно в двух планах – реальном и условном (игровом).

Поскольку игра представляет из себя «цепочку» проблемных ситуаций познавательного, практического, коммуникативного характера, она является психологическим эквивалентом творческой деятельности, а следовательно, формирует индивидуальный опыт такой деятельности. Существенно также то, что игра является средством развития умений и навыков коллективной мыследеятельности. Одновременно с этим она способствует развитию функций самоорганизации и самоуправления, снимает напряженность, позволяет проверить себя в различных ситуациях.

Классификация игр

1. По игровой методике: предметные, сюжетные, ролевые, деловые, имитационные, драматизация.

2. По характеру педагогического процесса: обучающие, познавательные, репродуктивные, коммуникативные, тренинговые, воспитательные, продуктивные, диагностические, контролирующие, развивающие, творческие, психотехнические, обобщающие.

3. По области деятельности: интеллектуальные, социальные, психологические, физические, трудовые.

4. По игровой среде: без предметов, с предметами, компьютерные, технические, настольные, телевизионные, со средствами передвижения, комнатные, ТСО, на местности.

Значение игровых форм и методов обучения

Ролевые, имитационные и другие игровые формы и методы обучения обеспечивают достижение ряда важнейших образовательных целей:

1. Стимулирование мотивации и интереса:

· в области предмета изучения;

· в общеобразовательном плане;

· в продолжении изучения темы;

2. Поддержание и усиление значения полученной ранее информации в другой форме, например:

· фактов, образа или системного понимания;

· расширенного осознания различных возможностей и проблем;

· последствий в осуществлении конкретных планов или возможностей;

3. Развитие навыков:

· критического мышления и анализа;

· принятия решений;

· взаимодействия, коммуникации;

· конкретных умений;

· готовности к специальной работе в будущем;

4. Изменение установок:

· социальных ценностей;

· восприятия интересов других участников, социальных ролей;

5. Саморазвитие или развитие благодаря другим участникам:

· оценка преподавателем тех же умений участника;

· осознание уровня собственной образованности, приобретение навыков, потребовавшихся в игре, лидерских качеств.

Структура организации игры

1. Выбор игры. На этом этапе происходит отбор содержания материала для игры на основе изучения программы, тематического плана, учебника, методической литературы. Отобрав игры, соответствующие программному материалу, я четко представляю себе, какие результаты я хочу получить, с тем чтобы в соответствии с этим выстроить замысел, игровые действия, формулировки правил игры и ее ход.

2. Подготовка игры:

- предварительная подготовка учащихся к игре, которая зачастую несет основную дидактическую нагрузку;

- подготовка непосредственно перед игрой, включающая создание эмоционального игрового настроения, планирование места проведения игры.

3. Введение в игру:

- объяснение правил игры, которые формулирую кратко и конкретно;

- выбор участников игры. Желательно в игре задействовать весь класс, так как на игровом уроке не должно быть пассивных зрителей. Я стараюсь организовывать командные или парные игры.

4. Ход игры:

- начало игры – этап уточнения нюансов игры, эмоциональный старт игры;

- развитие игрового действа и его кульминация;

- заключительный этап игры.

Учителю необходимо как барометру почувствовать спад настроения. Нужно научиться вовремя поставить точку, чтобы не только не пропало созданное игрой настроение, но и не расфокусировалось направленное на изучаемый учебный материал внимание.

5. Подведение итогов игры. Данный этап включает в себя как дидактический результат (что нового узнали, как справились с заданием, чему научились), так и собственно игровой (кто оказался лучшим, что помогло достичь победы).

6. Анализ игры проводится в разных формах: анкетирование учащихся, коллективное обсуждение, методика «Ваше настроение». Важно понимать, что проведение этого этапа – залог эффективности игровой деятельности на уроке и уровня методической подготовки учителя.

Игру я использую как средство обучения, воспитания и развития. Основное обучающее воздействие принадлежит дидактическому материалу, игровым действиям, которые как бы автоматически ведут учебный процесс, направляя активность учащихся в определенное русло.

Игровую форму занятий я использую на различных этапах урока. Целесообразность использования игры на различных этапах урока различна. Так, например, при усвоении новых знаний возможности игры значительно уступают более традиционным формам обучения. Поэтому игровые формы занятий чаще применяю при проверке результатов обучения, выработке навыков, формировании умений. В процессе игры у учащихся вырабатывается целеустремленность, организованность, положительное отношение к учебе.

Приведу пример использования игры «Математический поединок» в процессе усвоения формул сокращенного умножения.

В процессе игры происходит приобретение новых знаний, поэтому игру провожу на этапах урока по усвоению и закреплению знаний. Основой ее является соревнование между командами при ответах на вопросы и решении упражнений. Игровой замысел состоит в том, чтобы на основе созданной проблемной ситуации и соревнования команд активизировать мышление учащихся, превратить весь процесс обучения в процесс поисковой деятельности и самостоятельных открытий.

Для проведения игры класс делится на две команды. Выбираются капитаны команд и их ассистенты. Капитаны следят за порядком и дисциплиной в команде и сами участвуют в игре. Ассистенты при необходимости дают консультации. Разрешаются консультации также между учениками одной команды. Работа с ассистентами весьма эффективна, она позволяет организовать на уроке индивидуальный подход к учащимся; кроме того, ассистенты стремятся к тому, чтобы их работа в роли учителя и помощника капитана приносила успех команде. Ассистенты не освобождаются от общей работы класса и от ответов на вопросы.

При проведении урока должны соблюдаться следующие правила игры:

1. За правильный ответ команде начисляются очки; ошибка, допущенная в ответе, неправильный ответ, нарушение дисциплины приводят к штрафным очкам, то есть к снятию определенного количества очков со счета команды.

2. Каждый член команды может вновь отвечать только после того, как ответят все члены команды. Это исключает случаи, когда некоторые ученики за урок ни разу не опрашиваются.

3. Вопросы и задания дает учитель. Счет соревнования записывается на доске.

4. После постановки общего задания разрешаются консультации внутри команд.

5. Все необходимые записи по указанию учителя заносятся в тетрадь.

6. На определенном этапе работы сначала одна команда является «первопроходцем». Деятельность второй команды состоит в том, чтобы внимательно следить за правильностью ответов, выполнять по указанию учителя записи в тетрадях, а после завершения изучения некоторой части материала ответить на вопросы, предложенные учителем, и выполнить задания, аналогичные рассмотренным. Затем роли команд меняются.

7. За правильные аргументированные дополнения ответов учащихся из другой команды каждый может получить дополнительно 2 очка.

Игровые действия состоят в том, чтобы быстро и без ошибок отвечать на вопросы учителя, выполнять нужные записи и построения в тетрадях, следить за правильностью ответов своих товарищей из своей и другой команды, решать примеры и задачи у доски, во время объявленной консультации консультировать соседей по парте или при необходимости самому брать консультацию, не нарушать дисциплину, быть внимательным и активным.

Познавательное содержание состоит в том, чтобы учащиеся усвоили формулу сокращенного умножения 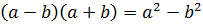и могли применять ее при умножении чисел и двучленов определенного вида.

Задания 1 команде.

· Выполнить устно умножение: .

· Найти значение числового выражения: .

· Объяснить используемы правила умножения.

Задания 2 команде аналогичны, меняются только упражнения.

Задания 2 команде.

· Выполнить устно умножение двучлена на одночлен: .

· Сформулировать распределительный закон умножения.

· Дать геометрическую интерпретацию распределительного закона.

Аналогичные задания предлагаются 1 команде.

Выполнение приведенных подготовительных упражнений детерминирует мысль учащихся, ставит вехи на пути к решению основной учебной проблемы.

Подводятся итоги первого этапа игры.

Учитель предлагает задание обеим командам одновременно: найти устно произведения 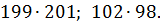Учащиеся не в состоянии выполнить вычисления. К удивлению класса, учитель быстро находит произведение записанных чисел. Учащиеся понимают, что имеющихся у них знаний недостаточно, чтобы справиться с поставленной задачей. Создается проблемная ситуация, связанная с желанием научиться устно находить произведение двух чисел.

Задание 2 команде.

Используя правило умножения двучлена на двучлен, найти произведение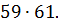

Один из учеников 2 команды записывает процесс решения данного упражнения на доске, а все остальные в тетрадях:

.

Другой ученик выполняет записи для примера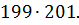

Аналогичные примеры выполняют учащиеся 1 команды.

Задание 1 команде.

Упростить записи в примерах данного вида. При умножении, например, 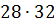учащиеся приходят к записи

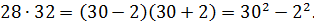
Аналогичный пример 2 команде.

Задания 1 команде.

· Найти произведение двучленов: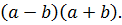

· Записать произведение суммы двух выражений на их разность, опустив промежуточные действия:

· Прочесть выражения: .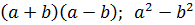

Аналогичные вопросы получает 2 команда.

Задание 2 команде.

Сформулировать правило сокращенного умножения суммы двух одночленов на их разность.

Такое же задание дается 1 команде.

Кульминационным моментом мышления в поисковой деятельности есть переход от конкретного примера 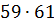к общей формуле.

Подводятся итоги второго этапа игры. Поощряются те ученики, которые дополняли ответы членов другой команды.

Дальше идет этап закрепления знаний.

Задание 1 команде: выполнить устно умножение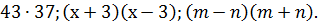

Задание 2 команде: выполнить устно умножение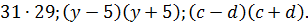

Задание 2 команде: Записать произведение в виде разности квадратов двух одночленов: .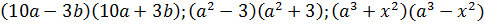

Задание 1 команде: записать произведение в виде разности квадратов двух одночленов: .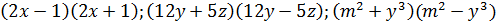

Поводятся итоги игры. Учащиеся выигравшей команды, принесшие команде наибольшее число очков, получают поурочный балл. При наличии времени продолжаю опрос на оценку или провожу самостоятельную работу. Ученики обеих команд, выполнившие работу, получают оценки.

Результат игры. Учащиеся обогатились знаниями и умениями применять формулу сокращенного умножения для умножения чисел и двучленов

Пояснительная записка

Увеличение умственной нагрузки на уроках математики заставляет задуматься над тем, как поддержать у учащихся интерес к изучаемому материалу, их активность на протяжении всего урока. В связи с этим основной проблемой, которую я ставила перед собой, работая над этой методической разработкой, состоит в том, чтобы отыскать новые эффективные методы обучения и такие методические приемы, которые активизировали бы мысль школьников, стимулировали бы их к самостоятельному приобретению знаний.

Возникновение интереса к математике у значительного числа учащихся зависит в большей степени от методики преподавания, от того, насколько умело будет построена учебная работа. Надо позаботиться о том, чтобы на уроках каждый ученик работал активно и увлеченно, и использовать это как отправную точку для возникновения и развития любознательности, глубокого познавательного интереса. Это особенно важно в подростковом возрасте, когда еще формируются, а иногда и только определяются постоянные интересы и склонности к тому или иному предмету. Именно в этот период нужно стремиться раскрыть притягательные стороны математики.

Немаловажная роль здесь отводится играм на уроках математики – современному и признанному методу обучения и воспитания, обладающему образовательной, развивающей и воспитывающей функциями, которые действуют в органическом единстве. В играх различные знания и новые сведения ученик получает свободно. Поэтому часто то, что на уроке казалось трудным, даже недостижимым, во время игры легко усваивается. Здесь интерес и удовольствие – важные психологические показатели игры.

Основная цель работы – активизация познавательной деятельности учащихся на уроках математики, развитие любознательности и глубокого познавательного интереса к предмету через игровую деятельность.

Как показывает педагогическая практика и анализ педагогической литературы, до недавнего времени игру использовали лишь на внеклассных занятиях по предмету, а возможности использования игры в учебном процессе в известной мере недооценивались.

Сказывалось отсутствие методических разработок по данному вопросу и постоянная нехватка личного времени учителя для создания игр, требующих повышенного методического и профессионального мастерства. Думается, что именно поэтому учителя математики не так уж часто допускают игру на уроке, хотя большинство из них выступают за привлечение в учебный процесс элементов игры. Поэтому при создании данной методической разработки я ставила перед собой задачи, отвечающие потребностям учителя при организации игровой деятельности на уроке.

Задачи:

- создание банка разных видов игр по математике для использования в учебном процессе, на примере которых можно было бы создавать подобные игры по различным темам курса математики и в разных классах;

- обучение учащихся самостоятельному приобретению знаний в процессе игры;

- обучение учащихся самостоятельно разрабатывать и изготавливать математические игры.

В данной методической разработке представлено теоретическое содержание, включающее способы организации разнообразных игр для уроков математики, требования к проведению игр на уроке, классификацию игр в зависимости от игровой цели, виды дидактических игр. Представлен дидактический материал, включающий разработки игр для применения их на уроках математики с подробным описанием правил организации и проведения, на примере которых можно создавать подобные игры по разным темам курса математики и в разных классах. Ко всем подобранным задачам даны ответы, что позволяет без труда составить контрольную карту. В работе приведен пример нетрадиционной формы урока, на котором еще и присутствует игра, что позволяет увидеть как включена игра в общее содержание урока, ее роль. Это делает данную методическую разработку удобной в применении для любого учителя математики, дает возможность учителям математики использовать новые методы преподавания и нетрадиционные формы уроков, возможность самим создавать дидактические игры и научить этому детей.

Эта тема была актуальна всегда не только для учителей математики.

Актуальность применения игровых технологий на уроках математики я вижу в том, что:

- игровые формы обучения на уроках создают возможности эффективной организации взаимодействия педагога и учащихся, продуктивной формы их общения с присущими им элементами соревнования, непосредственности, неподдельного интереса;

- в игре заложены огромные воспитательные и образовательные возможности;

- в процессе игр дети приобретают самые различные знания о предметах и явлениях окружающего мира;

- игра развивает детскую наблюдательность и способность определять свойства предметов, выявлять их существенные признаки;

- игры очень хорошо уживаются с “серьезным” учением;

- включение в урок игр и игровых моментов делает процесс обучения интересным и занимательным, создает у детей бодрое рабочее настроение, облегчает преодоление трудностей в усвоении учебного материала;

- разнообразные игровые действия, при помощи которых решается та или иная умственная задача, поддерживают и усиливают интерес детей к учебному предмету.

- игры оказывают большое влияние на умственное развитие детей, совершенствуя их мышление, внимание, творческое воображение.

Известный французский ученый Луи де Бройль утверждал, что все игры (даже самые простые) имеют много общих элементов с работой ученого. В игре привлекает поставленная задача и трудность, которую можно преодолеть, а затем радость открытия и ощущение преодоленного препятствия. Именно поэтому всех людей, независимо от возраста, привлекает игра.

Назначение игр на уроках математики – развитие познавательных процессов у школьников (восприятия, внимания, памяти, наблюдательности, сообразительности и др.) и закрепление знаний, приобретаемых на уроках.

Характерным для каждой игры является, с одной стороны, решение различных дидактических задач: уточнение представлений о числе или в целом о математическом понятии и его существенных особенностях, развитие способности замечать сходство и различие между ними и т.д. В этом смысле игра носит обучающий характер.

С другой стороны, неотъемлемым элементом игры является игровое действие. Внимание ученика направлено именно на него, а уже в процессе игры он незаметно для себя выполняет обучающую задачу.

В настоящее время наука педагогика внесла большой вклад в развитие и разработку проблемы игры в школе, по-новому подошла к решению многих вопросов: придала исключительное значение содержанию игры, признала настоятельной необходимостью использование игровых технологий при изучении всех предметов в школе, что дает возможность учителям использовать новые методы преподавания и нетрадиционные формы уроков, повышающие интерес учащихся к учебе и эффективность учебных занятий.

Содержание

На уроках математики игра приобретает особенное значение, как писал Я.И. Перельман, не столько для друзей математики, сколько для ее недругов, которых важно не приневолить, а приохотить к учению. Дидактическая игра (большинство учителей, методистов и дидактов игру, которая проводится в процессе обучения, называют дидактической) – не самоцель на уроке, а средство обучения и воспитания. Игру не нужно путать с забавой, не следует рассматривать ее как деятельность, доставляющую удовольствие ради удовольствия. На дидактическую игру нужно смотреть как на вид преобразующей творческой деятельности в тесной связи и системе с другими формами обучения, использование которых должно в конечном итоге привести к решению следующих задач: учитель должен дать учащимся знания, соответствующие современному уровню развития науки; он должен их научить самостоятельно приобретать знания.

Анализ психолого – педагогической литературы по этому вопросу, наблюдения за игровыми действиями, вводимыми в учебный процесс, а также осмысление накопленного опыта позволяют выделить следующие виды дидактических игр:

- игры – упражнения;

- игры – путешествия;

- сюжетная (ролевая) игра;

- игра – соревнование.

Игры – упражнения. Они занимают обычно 10 – 15 минут и направлены на совершенствование познавательных способностей учащихся, являются хорошим средством для развития познавательных интересов, осмысления и закрепления учебного материала, применения его в новых ситуациях. Это разнообразные викторины, кроссворды, ребусы, чайнворды, шарады, головоломки, загадки.

Игры – путешествия. Они служат, в основном, целям углубления, осмысления и закрепления учебного материала. Активизация учащихся в играх – путешествиях выражается в устных рассказах, вопросах, ответах.

Сюжетная (ролевая) игра отличается тем, что инсценируются условия воображаемой ситуации, а учащиеся играют определенные роли.

Игра – соревнование может включать в себя все вышеназванные виды дидактических игр или их отдельные элементы. Для проведения этого вида игры учащиеся делятся на группы, команды, между которыми идет соревнование. Существенной особенностью игры – соревнования является наличие в ней соревновательной борьбы и сотрудничества. Элементы соревнования занимают ведущее место в основных игровых действиях, а сотрудничество, как правило, определяется конкретными обстоятельствами и задачами. Игра – соревнование позволяет учителю в зависимости от содержания материала вводить в игру не просто занимательный материал, но весьма сложные вопросы учебной программы. В этом ее основная педагогическая ценность и преимущество перед другими видами дидактических игр.

В реальной практике обучения все виды игр могут выступать и как самостоятельные, и как взаимно дополняющие друг друга. Использование каждого вида игр и их разнообразных сочетаний определяется особенностями учебного материала, возрастом учащихся и другими педагогическими факторами.

Требования к организации игры на уроке:

- Игра должна быть построена на интересе.

- Игра должна основываться на свободном творчестве и самостоятельной деятельности учащихся. Различные виды занятий по математике и на уроках и во внеклассной работе, конечно, тоже не лишены творчества, но в игре творчество учащихся особенно необходимо. Это не значит, что участники игры не имеют никаких обязанностей. Опыт показывает, что часто ученики относятся к этим обязанностям серьезнее, с чувством большей ответственности, чем в учебной или трудовой деятельности.

- Игра должна быть доступной для учащихся данного возраста, цель игры – достижимой, а оформление – красочным и разнообразным.

- Обязательный элемент игры – ее эмоциональность. Игра должна вызывать удовольствие, веселое настроение, удовлетворение от удачного ответа.

- В играх обязателен элемент соревнования между командами или отдельными участниками игры. Это всегда приводит к повышению самоконтроля учащихся, к четкому соблюдению установленных правил и, главное, к активизации учащихся. В этом случае завоевание победы для выигрыша – очень сильный мотив, побуждающий ученика к деятельности.

- Особо важна роль активности учащихся во время проведения игры. В противном случае учитель не получит желаемого результата от урока, а время, отведенное на игру, окажется просто потерянным.

- Говоря о большом воспитательном и познавательном значении математических игр, следует указать на важную роль учителя при их организации. Прежде всего, учитель должен положить начало творческой работе учащихся, но контроль и руководство учителя не должны превращаться в подавление инициативы и самостоятельности детей, иначе будет уничтожена самая сущность игры, которая невозможна без свободного проявления личности учащегося. Постепенно учитель может отойти от роли ведущего, уступая ее хорошо подготовленным ученикам.

- Многие игры учащиеся могут разрабатывать и изготавливать самостоятельно. Для этого можно объявить конкурс на лучшую игру. Каждую придуманную игру нужно проверять в действии.

- Большинство игр по математике с раздаточным материалом требуют специальной контрольной карты, куда включены не только правила игры, но и предполагаемые ответы учащихся. Учитель может поручить учащимся составление таких карт. Игру следует считать подготовленной только в том случае, если к ней составлена контрольная карта.

- Дидактические игры должны быть очень разнообразными как по содержанию, так и по форме проведения.

Этапы игры включают:

1. Предварительную подготовку: класс разбивается на команды (если нужно), примерно равные по способностям, даются домашние задания командам.

2. Игру.

3. Заключение по уроку: выводы о работе участников игры и выставление оценок.

Примеры таких видов игр, которые более приемлемы на уроках математики, я привожу в данной методической разработке. Для создания некоторых из них я использовала идеи телевизионных игр. Их смотрят дети, значит, они им будут более понятны и интересны, и они хорошо вписываются в урок по времени и содержанию.

Игра “Поле чудес”.

Правила игры:

Учитель берет понравившееся ему высказывание или слова из песни, стихотворения, пословицу. По количеству букв в этом высказывании подбирается столько же задач так, чтобы одинаковым буквам соответствовали одинаковые ответы. Готовятся карточки желательно с дифференцированными заданиями, которые выдаются каждому ученику. На доске заранее должны быть записаны буквы, которые встречаются в высказывании, и под ними ответы, которые будут соответствовать этим буквам. Ниже должны быть записаны числа по порядку (по количеству букв в высказывании), соответствующие номерам карточек. Ученик, выполнивший задание, называет номер своей карточки и букву, под которой записан ответ. Например, карточка №5, буква А. Учитель под числом 5 ставит букву А. Если у ученика получилась другая буква, значит он решил неверно, и у него есть время перерешать задачу, пока другие ребята еще решают свои задания. Те учащиеся, которые быстро справляются с заданием, получают следующую карточку. За правильно решенные 1-3 задания (на усмотрение учителя) ученик может получить оценку. Поэтому желательно карточек иметь больше, чем число учеников в классе.

Пример игры. Тема: “ Теорема Пифагора”. 8 класс.

Задания:

1. В прямоугольной трапеции основания равны 5 и 17 см, а большая боковая сторона 13 см. Найдите площадь трапеции. (55).

2. В треугольнике два угла равны 45° и 90°, а большая сторона 5832 см. Найдите две другие стороны треугольника. (54).

3. В прямоугольной трапеции основания равны 12 и 6 см, а большая боковая сторона 10 см. Найдите площадь трапеции. (72).

4. В треугольнике ABC ÐA=90°, ÐC=30°, AB=6 см. Найдите сторону AC треугольника. (6Ö3).

5. В прямоугольной трапеции боковые стороны равны 5 и 3 см, а большее основание 20 см. Найдите площадь трапеции. (54).

6. Диагонали ромба равны 14 и 48 см. Найдите сторону ромба. (25).

7. В равнобедренном треугольнике угол при основании 45°, а высота, проведенная к основанию, равна 8 см. Чему равна площадь треугольника? (64).

8. Боковая сторона равнобедренного треугольника рана12 см, а основание равно 12Ö3 см. Найдите высоту, проведенную к основанию. (6).

9. В прямоугольном треугольнике катеты равны по 6 см. Чему равна высота, проведенная к основанию? (3Ö2).

10. Найдите площадь равнобедренного треугольника, если его основание равно 24 см, а боковая сторона равна 6Ö5 см. (72).

11. В равностороннем треугольнике сторона равна 8 см. Найдите высоту треугольника. (4Ö3).

12. Найдите катет прямоугольного треугольника, если его гипотенуза равна 10 см, а другой катет равен 8 см. (6).

13. Стороны прямоугольника рваны 8 и 6 см. Найдите его диагональ. (10).

14. Найдите гипотенузу прямоугольного треугольника, если его катеты равны 3Ö3 см и 3 см. (6).

15. Найдите гипотенузу прямоугольного треугольника, если его катеты равны 7 см и 24 см. (25).

16. Площадь прямоугольного треугольника равна 18Ö2, катет его равен 6. Найдите гипотенузу. (6Ö3).

17. Вычислить площадь равнобедренного треугольника с боковой стороной 3 см и основанием 2 см. (2Ö2).

18. Найдите катет прямоугольного треугольника, лежащий против угла 60°, если гипотенуза равна 8 см. (4Ö3).

19. В треугольнике ABC ÐB=45°, а высота AN делит сторону BC на отрезки BN=8 см и NC=6 см. Найдите сторону AC. (10).

20. Найдите площадь равностороннего треугольника, сторона которого равна 12 см. (36Ö3).

21. В равнобедренном прямоугольном треугольнике гипотенуза равна 14 см. Чему равны катеты этого треугольника? (7Ö2).

22. Найдите гипотенузу прямоугольного треугольника, если его катеты равны 4Ö2 см и 2 см. (6).

23.В прямоугольной трапеции боковые стороны равны 7 и 25см, а меньшее основание равно 2 см. Найдите площадь трапеции. (98).

Контрольная карта:

Дата добавления: 2015-09-03