Курсова робота

На тему:

«Побудова зображень в лінзах та сферичних дзеркалах»

Виконав:

Лiцеїст 10-Г-1 класу

Швець Микита Сергiйович

Керівник:

Кандидат фізико-технічних наук

Могилевська Наталія Володимирівна

Дніпропетровськ

2012

Зміст

Вступ. 3

Лінза. 4

Iсторiя. 6

Характеристики простих лінз 7

Формула тонкої лінзи. 11

Побудова зображення тонкою збиральною лінзою.. 13

Розрахунок фокусної відстані і оптичної сили лінзи. 19

Застосування лінз 21

Недоліки лінз 22

Цiкавi факти. 24

Дзеркало. 25

Побудова зображення у плоскому дзеркалi 28

Застосування плоских дзеркал. 30

Сферичне дзеркало. 31

Побудова зображення в сферичному дзеркалі 32

Застосування сфериних дзеркал. 36

Загадки увігнутих дзеркал (поряд зі звичною фізикою) 41

Параболічне і еліптичне дзеркало. 45

Список використаної літератури. 46

Вступ

Моя курсова робота присвячена вивченню лінз та дзеркал, та побудові зображення у них.

Я вибрав саме цю тему тому, що геометрична оптика вивчалася в сьомому класі, і розглядалася там дуже мало. Насправді ця тема дуже цікава та корисна у разі поглиблення у неї. Саме про геометричну оптику я і хочу розповісти.

Мета роботи полягає в тому, щоб навчитися будувати зображення в різних видах лінз та дзеркал, описати та змоделювати процеси побудови зображень.

Моя робота може бути корисною і використана в навчальному процесі при вивчені побудови зображень в лінзах та сферичниз дзеркалах.

Лінза

Лінза (нім. Linse, від лат. Lens - чечевиця) - деталь з оптично прозорого однорідного матеріалу, обмежена двома полірованими заломлюючими поверхнями обертання, наприклад, сферичними або плоскою і сферичною. В даний час все частіше застосовуються і «асферичні лінзи», форма поверхні яких відрізняється від сфери. Як матеріал лінз використовуються оптичні матеріали, такі як скло, оптичне скло, оптично прозорі пластмаси та інші матеріали.

Рис. 1. Двоопуклa лінзa

Лінзами також називають і інші оптичні прилади та явища, які створюють подібний оптичний ефект, не володіючи зазначеними зовнішніми характеристиками, наприклад:

· Плоскі «лінзи», виготовлені з матеріалу з змінним коефіцієнтом заломлення, що змінюється в залежності від відстані від центру.

· Лінзи Френеля.

· Зонна пластинка Френеля, що використовує явище дифракції.

· «Лінзи» повітря в атмосфері - неоднорідність властивостей, зокрема, коефіцієнта заломлення (проявляються у вигляді мерехтіння зображення зірок у нічному небі).

· Гравітаційна лінза - спостережуваний на міжгалактичних відстанях ефект відхилення електромагнітних хвиль масивними об'єктами.

· Магнітна лінза - пристрій, що використовує постійне магнітне поле для фокусування пучка заряджених частинок (іонів або електронів) і застосовується в електронних і іонних мікроскопах.

· Зображення лінзи, сформоване оптичною системою або частиною оптичної системи. Використовується при розрахунку складних оптичних систем.

Iсторiя

Перше згадування про лінзи можна знайти в давньогрецькій п'єсі Арістофана "Хмари" (424 до н. е.), де за допомогою опуклого скла і сонячного світла добували вогонь.

З творів Плінія Старшого (23 – 79) випливає, що такий спосіб розпалювання вогню був відомий і в Римській імперії - там також описаний, можливо, перший випадок застосування лінз для корекції зору - відомо, що Нерон дивився гладіаторські бої через увігнутий смарагд для виправлення короткозорості.

Сенека (3 до н. е. - 65) описав збільшувальний ефект, який дає скляна куля, заповнена водою.

Арабський математик Альхазен (965-1038) написав перший значний трактат з оптики, який описує, як кришталик ока створює зображення на сітчатці. Лінзи отримали широке використання лише з появою окуляр приблизно в 1280-х роках в Італії.

Характеристики простих лінз

Залежно від форм розрізняють збиральнi (додатні) і розсіюючі (від’ємнi) лінзи. До групи збиральних лінз зазвичай відносять лінзи, у яких середина товща їх країв, а до групи розсіюючих - лінзи, краї яких товщі середини. Слід зазначити, що це вірно тільки якщо показник заломлення у матеріалу лінзи більше, ніж у навколишнього середовища. Якщо показник заломлення лінзи менше, ситуація буде зворотньою. Наприклад бульбашка повітря у воді - двоопукла розсіююча лінза.

Рис. 2. Крізь краплі дощу, що діють як лінзи, видно Золоті Ворота

Рис. 3. Рослина, видимa через двоопуклу лінзу

Лінзи характеризуються, як правило, своєю оптичною силою (вимірюється в діоптріях), або фокусною відстанню.

Для побудови оптичних приладів з виправленою оптичною аберацією (насамперед - хроматичною, зумовленою дисперсією світла, - ахромати і апохромати) важливі й інші властивості лінз і їх матеріалів, наприклад, коефіцієнт заломлення, коефіцієнт дисперсії, коефіцієнт пропускання матеріалу в обраному оптичному діапазоні.

Іноді лінзи / лінзові оптичні системи (рефрактори) спеціально розраховуються на використання в середовищах з відносно високим коефіцієнтом заломлення.

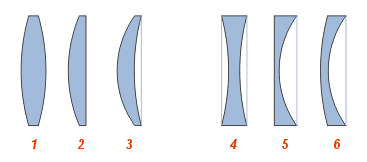
Рис.4. Види лінз

Види лінз:

збиральнi:

1 - двоопукла

2 - плоско-опукла

3 - увігнуто-опукла (додатнiй (опуклий) меніск)

розсіюючі:

4 - двоякоувiгнута

5 - плоско-увігнута

6 - опукло-увігнута (від'ємний (увігнутий) меніск)

Опукло-увігнута лінза називається меніском і може бути збиральною (потовщується до середини), розсіюючою (потовщується до країв) або телескопічною (фокусна відстань дорівнює нескінченності). Так, наприклад лінзи окулярів для короткозорих - як правило, від'ємні меніски.

Всупереч поширеній помилці, оптична сила меніска з однаковими радіусами не дорівнює нулю, а додатня, і залежить від показника заломлення скла і від товщини лінзи. Меніск, центри кривизни поверхонь якого знаходяться в одній точці називається концентричній лінзою (оптична сила завжди від'ємна).

Якщо на скляну лінзу, що знаходиться в повітрі, направити параксіальний пучок світла паралельно головній оптичній осі, то в опуклій лінзі пучок збереться у точці F (Рис. 5), яку називають головним фокусом. Такі лінзи відносять до збиральних. Якщо такий пучок направити на увігнуту лінзу (Рис. 6), то пучок розсіюється так, що проміні ніби то виходять з точки F, яку називають уявним головним фокусом лінзи.

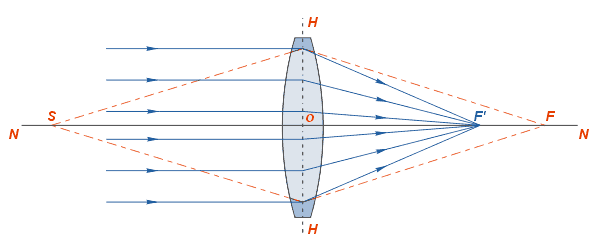
Рис. 5. Дійсний фокус збиральної лінзи

Основні елементи лінзи:

· NN – головна оптична вісь - пряма лінія, що проходить через центри сферичних поверхонь, що обмежують лінзу;

· т.O - оптичний центр - точка, яка у двоопуклих або двоввігнутих (з однаковими радіусами поверхонь) лінз знаходиться на оптичній осі всередині лінзи (в її центрі).

Примітка. Хід променів показаний, для ідеалізованої (тонкої) лінзі, без вказівки на заломлення на реальній межі розділу середовищ.

Рис. 6. Уявний фокус розсіюючої лінзи

Формула тонкої лінзи

Відстані від точки предмета до центру лінзи і від точки зображення до центру лінзи називаються сполученими фокусними відстанями.

Рис. 7. Зображення предмета в збиральній лінзі, d > 2F

Ці величини знаходяться в залежності між собою і визначаються формулою, званої формулою тонкої лінзи (відкритої Ісааком Барроу):

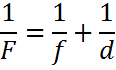
де d — відстань від лінзи до предмета; f — відстань від лінзи до зображення; F — головна фокусна відстань лінзи. У разі товстої лінзи формула залишається без зміни з тією лиш різницею, що відстані відлічуються не від центру лінзи, а від головних площин.

Для знаходження тієї чи іншої невідомої величини при двох відомих користуються такими рівняннями:

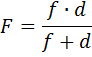
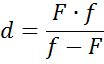
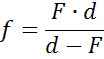
Слід зазначити, що знаки величин d, f, F вибираються виходячи з таких міркувань - для дійсного зображення від дійсного предмета в збиральнiй лінзі - всі ці величини позитивні. Якщо зображення уявне - відстань до нього приймається вiд'ємною, якщо предмет уявний - відстань до нього вiд'ємна, якщо лінза розсіююча - фокусна відстань вiд'ємна.

Побудова зображення тонкою збиральною лінзою

При викладенні характеристики лінз був розглянутий принцип побудови зображення світящої точки у фокусі лінзи. Промені, які падають на лінзу ліворуч, проходять через її задній фокус, а падаючі справа - через передній фокус. Слід врахувати, що у розсіюючих лінз, навпаки, задній фокус розташований спереду лінзи, а передній позаду.

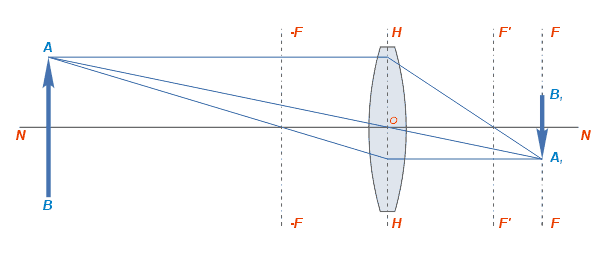
Побудова лінзою зображення предметів, що мають певну форму і розміри, виходить так: припустимо, лінія AB являє собою об'єкт, що знаходиться на деякій відстані від лінзи, значно перевищуючiй її фокусну відстань. Від кожної точки предмета через лінзу пройде незліченна кількість променів, з яких, для наочності, на малюнку схематично зображено хід тільки трьох променів:

а) промінь, паралельний головній оптичній осі; після преломлення він пройде через головний фокус

б) промінь, співпадаючий з побічною оптичною віссю; проходить без преломлення через центр лінзи

в) промінь, що проходить через головний фокус; після переломлення він іде паралельно головній оптичній осі

Три промені, що виходять з точки A, пройдуть через лінзу і перетнуться у відповідних точках сходу А₁В₁. Опускаємо перпендикуляр на головну оптичну вісь, утворюючи зображення. Якщо предмет має більш складну форму, треба тим же способом побудувати зображення основних точок, що визначають форму предмета.

Отримане зображення є дійсними перевернутим. В даному випадку зображення отримано в зв'язаному фокусі в деякій фокальній площині FF, кілька віддаленої від головної фокальної площини F'F ', що проходить паралельно їй через головний фокус.

Далі наведені різні випадки побудови зображень предмета, розміщеного на різних відстанях від лінзи.

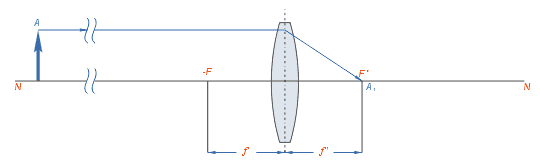
Мал.3)

d=

Зображення дійсне, перевернуте і зменшене до подібності точки (мал.3).

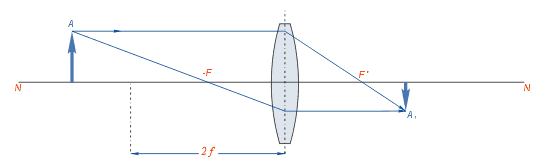
Мал.4)

d > 2F

Зображення дійсне, перевернуте, зменшене (мал. 4).

F < f < 2F

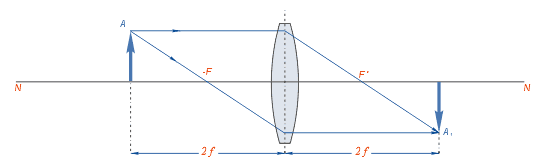
Мал.5)

d = 2F

Зображення дійсне, обернене, рівне (мал.5).

f = 2F

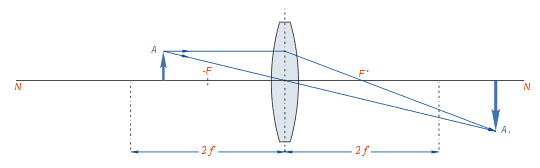
Мал.6)

2F > d > F

Зображення дійсне, обернене, збільшене (мал.6).

f > 2F

Мал.7)

d = F

Зображення знаходиться в нескінченності (мал.7).

f =

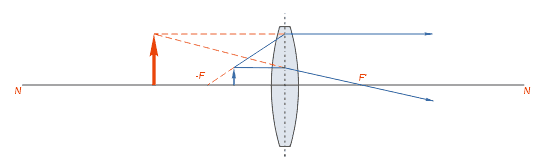
Мал.8)

d < F

Зображення уявне, збульшене, пряме (мал.8).

f > 2F

Неважко помітити, що при наближенні предмета з нескінченності до переднього фокусу лінзи зображення віддаляється від заднього фокусу і після досягнення предметом площини переднього фокуса виявляється у нескінченності від нього.

Ця закономірність має велике значення в практиці різних видів фотографічних робіт, тому для визначення залежності між відстанню від предмета до лінзи і від лінзи до площини зображення необхідно знати основну формулу лінзи.

Розсіююча лінза дає пряме, уявне, зменшене зображення предмета(мал. 9)

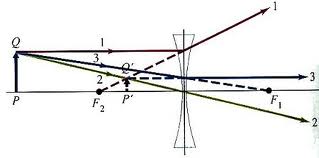
Мал. 9)

Розрахунок фокусної відстані і оптичної сили лінзи

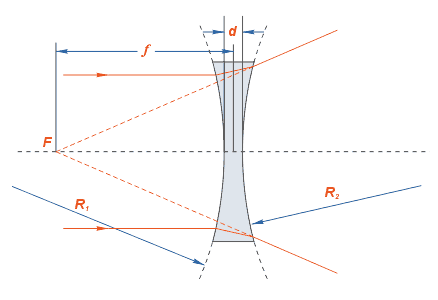
Значення фокусної відстані для лінзи може бути розраховано за формулою:

, де

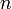—коефіцієнт переломлення матеріалу лінзи,

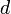— відстань між сферичними поверхнями лінзи вздовж оптичної осі, також відоме як товщина лінзи, а знаки при радіусах вважаються додатнiми, якщо центр сферичної поверхні лежить праворуч від лінзи і вiд'ємними, якщо зліва. Якщо 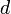зневажливо мало, щодо її фокусної відстані, то така лінза називається тонкою, і її фокусну відстань можна знайти так:

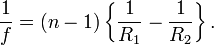
де R > 0 якщо центр кривизни знаходиться праворуч від головної оптичної осі; R < 0 якщо центр кривизни знаходиться ліворуч від головної оптичної осі. Наприклад, для двоопуклої лінзи буде виконуватися умова 1 / F = (n-1) (1/R1 +1 / R2)

(Цю формулу також називають формулою тонкої лінзи.) Величина фокусної відстані додатня для збираючих лінз, і вiд'ємна для розсіюючих. Величина 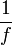називається оптичною силою лінзи. Оптична сила лінзи вимірюється в діоптріях, одиницями вимірювання яких є м ⁻¹.

Зазначені формули можуть бути отримані акуратним розглядом процесу побудови зображення в лінзі з використанням закону Снелла, якщо перейти від загальних тригонометричних формул до параксіального наближення.

Лінзи симетричні, тобто вони мають однакову фокусну відстань незалежно від напрямку світла - зліва чи справа, що, однак, не відноситься до інших характеристик, наприклад, аберація, величина яких залежить від того, яким боком лінза повернена до світла.

Застосування лінз

ü Лінзи є універсальним оптичним елементом більшості оптичних систем.

ü Традиційне застосування лінз - біноклі, телескопи, оптичні приціли, теодоліти, мікроскопи і фотовідеотехніка. Одиночні збираючі лінзи використовуються як збільшувальне скло.

ü Інша важлива сфера застосування лінз офтальмологія, де без них неможливо виправлення недоліків зору - короткозорості, далекозорості, неправильної акомодації, астигматизму і інших захворювань. Лінзи використовують в таких пристроях, як окуляри й контактні лінзи.

ü У радіоастрономії і радарах часто використовуються діелектричні лінзи, що збирають потік радіохвиль в приймальню антену, або фокусують на цілі.

ü У конструкції плутонієвих ядерних бомб для перетворення сферичної розбіжної ударної хвилі від точкового джерела (детонатора) в сферичну сходячу застосовувалися лінзові системи, виготовлені з вибухівки з різною швидкістю детонації (тобто з різним коефіцієнтом заломлення).

Недоліки лінз:

Деяким лінзам характерні деякі дефекти:

· Хроматична аберація. Через дисперсію в лінзі виникає розклад білого кольору в спектр. При цьому червоні промені, переломлюючись слабкіше, фокусуються далі від центру лінзи; сині та фіолетові, переломлюючись сильніше, фокусуються ближче. В результаті хроматичної аберації зображення у лінзі виявляється розмитим та забарвленим. Виправлення: за допомогою подвійної лінзи, підібравши різні сорти скла з різною дисперсією. Лінзи, в яких усунена хроматична аберація, називаються ахроматами. Такі лінзи використовують як об’єктиви телескопів-рефракторів, гарних біноклів, найпростіших фотоапаратів і т.д.

· Сферична аберація. У товстих лінзах промені, які пройшли у країв лінзи, сходяться в іншій точці, ніж промені, які пройшли ближче до її центру. промені, переломившись в лінзі, не сходяться в одній точці; замість зображення предмета (точки) виходить розмита пляма. Зображення не чітке.

Виправлення: Використання тільки параксіальних пучків, тобто пучків, близьких до головної оптичної осі. Для цього лінзу дефрагментують, пропускаючи через неї більш вузький пучок. Але цим зменшується енергія пучка та освітлення зображення. Другий спосіб послаблення сферичної аберації випливає з того, що у збираючих та розсіюючи лінз оптична сила має протилежні знаки, і можна підібрати таку пару лінз (мал. 10), щоб їх аберації суттєво компенсувалися.

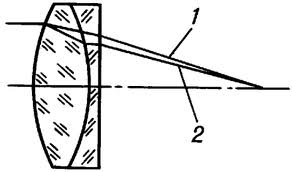
Мал. 10)

· Значні аберації також з’являються при падінні на лінзу променів під великим кутом до оптичної осі. Виправлення цих аберацій можливе шляхом підбору системи з декількох(до десятка) лінз, кожна з котрих компенсує недоліки іншої.

· Викривлення площині зображення. У товстих лінз поверхню зображення не плоска, це веде до діжкоподібним або подушкообразному викривленнi. Виправлення: особлива комбінація лінз, апланат.

· Астигматизм. Розмиття внаслідок похилого падіння світлового пучка. Комбінація лінз, яка виправляє цей недолік, називається анастигмати.

Цiкавi факти

· При житті Ньютон найбільше був відомий своїми дослідженнями в області оптики. А його праця «Оптика» протягом десятиліть вважалася енциклопедією наукиспро світло.

· У Сіракузах, де за легендою Архімед підпалював за допомогою дзеркал ворожі кораблі, йому було встановлено пам'ятник, що зображає ученого зі сферичним дзеркалом у руках, спрямованим в бік моря.

· Леонардо да Вінчі писав свої трактати перевернутим шрифтом за допомогою дзеркала. Його рукописи вперше були розшифровані лише три сторіччя потому.

· Перший оптичний Семафорний телеграф пов'язав в кінці 17 століття Париж з містом Ліллем. До середини 19 століття в Росії діяло вже кілька оптичних телеграфних ліній, найбільшою з яких була лінія Петербург - Варшава, яка мала 149 проміжних пунктів. Сигнал між цими містами проходив всього за кілька хвилин, причому тільки вдень і при хорошій видимості.

· Живі дзеркала - світящi в темряві очі кішки або блискуча риб'яча луска, що переливається всіма барвами веселки - це добре відбиваючi світло поверхні.

· У деяких тварин робота ока заснована на дзеркальній оптиці. Природа створила багатошарові дзеркала. Важливою структурою ока, що поліпшує нічний зір багатьох наземних тварин, що ведуть нічний спосіб життя - це плоске багатошарове дзеркальце «тапетум», завдяки якому і світяться в темряві очі. Тому око кішки може бачити навколишні предмети при освітленості в 6 разів меншiй, ніж потрібно людині. Таке ж дзеркальце виявлено у деяких риб.

Дзеркало

Дзеркало - гладка поверхня, призначена для відбиття світла (або іншого випромінювання). Найбільш відомий приклад - плоске дзеркало.

Принцип ходу променів, відбитих від дзеркала простий, якщо застосовувати закони геометричної оптики, не враховуючи хвильову природу світла. Промінь світла падає на дзеркальну поверхню (розглядаємо повністю непрозоре дзеркало) під кутом альфа до нормалі (перпендикуляру), проведеної до точки падіння променя на дзеркало. Кут променя відбитого буде дорівнює тому ж значенню-альфа. Промінь, падаючий на дзеркало під прямим кутом до площини дзеркала, відіб'ється сам в себе.

Плоске дзеркало

Плоске дзеркало – плоска гладенька поверхня, що дозволяє дзеркально відбивати світло.

З життєвого досвіду ми добре знаємо, що наші зорові враження часто виявляються помилковими. Іноді навіть важко буває відрізнити удаване світлове явище від дійсного. Прикладом обманливого зорового враження служить уявне зорове зображення предметів за плоскою дзеркальною поверхнею.

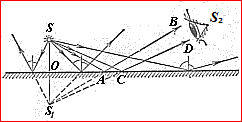Розглянемо приклад відображення світла в плоскому дзеркалі.

Точка S₁ є уявним зображенням точки S₁. Така назва зв’язана з тим, що в точку S₁ не попадає енергія від джерела світла. Її положення визначається перетинанням будь-яких двох променів, що потрапляють в око, наприклад AB і CD. Лінія SS₁ перпендикулярна до площини дзеркала, причому OS = OS₁. Для того, щоб знайти зображення точки в плоскому дзеркалі, досить на перпендикулярі, опущеному з точки на дзеркало, відкласти за дзеркалом таку ж відстань.

Якщо розташувати око в області відбитого світлового пучка і поглянути на дзеркало, виникне зорова ілюзія: нам буде здаватися, що за дзеркалом знаходиться джерело світла S₁. Чому ж ми бачимо уявне зображення? Справа у тому, що кришталик ока та скловидне тіло збирають розбіжний світловий пучок сітківці в точці S₂. Аналогічно розбіжний пучок може зібрати об’єктив фотоапарату. Саме властивість лінз збирати розбіжний пучок дозволяє бачити уявне зображення. Оптика фотоапарату збирає розбіжний пучок, тому фотоапарат також здатний фіксувати уявне зображення.

Уявне зображення предмета в плоскому дзеркалі завжди пряме, але повернене до предмета, так би мовити, лицем до лиця. Це означає, що уявне зображення предмета і сам предмет симетричні відносно площини дзеркала. Зображення предмета в плоскому дзеркалі одно за розміром самому предмету.

Побудова зображення у плоскому дзеркалi

Як же формується зображення предмета в дзеркалі?

Будь-який предмет складається з безлічі точок, тому досить дізнатися, як виникає зображення хоча б однієї точки.

Побудуємо зображення точкового джерела світла (S) в дзеркалі. Для цього достатньо простежити хід двох світлових променів. Зображення точки (S штрих) має з'явитися на перетині цих променів або їх продовжень.

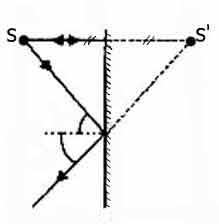
Беремо найпростіший для побудови промінь - промінь, що падає перпендикулярно на поверхню дзеркала, другий промінь-довільний. Відбиті промені будуємо за законом відображення. Перетнутися в даному випадку можуть тільки продовження променів.

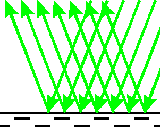Зображення в плоскому дзеркалі уявне ("за дзеркалом"), пряме (неперевернуте), в натуральну величину і розташоване симетрично джерелу відносно площини дзеркала.

Більшість дзеркал виготовляється з дуже гладкого скла, покритого із зворотнього боку тонким шаром добре відбиваючого металу, тому практично все падаюче на дзеркало світло відбивається в одному напрямку. Будь-які інші гладкі поверхні (поліровані, лаковані, спокійна водна поверхня) теж можуть дати дзеркальне відображення. Якщо гладка поверхня ще й прозора, то лише невелика частина світла відіб'ється, і зображення не буде таким яскравим.

Якщо поверхня дзеркала вигнута, то зображення буде спотвореним ("криве дзеркало").

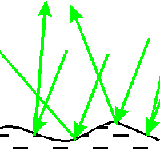Зовсім інше віддзеркалення виходить від шорсткуватої поверхні. Через нерівності поверхні відбиті промені спрямовані в різні сторони. Така поверхня дає розсіяне світло (дзеркального відображення не буде).

Застосування плоских дзеркал

· Ми навіть не помічаємо, що постійно використовуємо плоскі дзеркала в побуті починаючи від маленьких дзеркал на точила і закінчуючи великими трюмо.

· Завдяки відображенню світлового променя від плоского дзеркала можна здійснювати світлову сигналізацію. Приймач випромінювання вловлює відбитий промінь. Якщо цього не відбувається (щось завадило ходу світлового променя), то спрацьовує тривога.

· Прямі дзеркала використовуються в перископ підводних човнів. Це дозволяє спостерігати з під води за тим, що відбувається на поверхні.

· Багаторазові відбиття світла паралельними дзеркалами використовується в інтерферометра Фабрі-Перо, де дзеркалами служать паралельні кварцові пластини з нанесеними на них металевими або багатошаровими діелектричними відбиваючими покриттями.

Сферичне дзеркало

Сферичне дзеркало -дзеркало, відбиваюча поверхня якого має вид сегмента сфери.

Приклад зображення в опуклому дзеркалі.

Художник Пармиджанино. Автопортрет в опуклому дзеркалі.

1524г. Відень

Сферичне дзеркало може бути опуклим або вгнутим - залежно від того, яка сторона сегмента сфери - опукла або увігнута - є відбиваючою. Центр відповідної сферичному дзеркалу сфери називається його центром або оптичним центром, середина сегмента - полюсом дзеркала, пряма, що проходить через центр і полюс - головною оптичною віссю дзеркала. Інші прямі, що проходять через центр дзеркала і точку, що відрізняється від полюса, називаються його побічними оптичними осями.

Параксіальнi промені, паралельні головній оптичній осі опуклого сферичного дзеркала, так само як і продовження параксіальних променів, паралельних головній оптичній осі увігнутого сферичного дзеркала, перетинаються в одній точці, яка називається його фокусом. Він розташований посередині між центром і полюсом дзеркала, тобто відстань (f) його до дзеркала дорівнює половині радіуса (R):

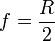
Побудова зображення в сферичному дзеркалі

У житті ви часто бачили своє спотворене відображення на опуклій поверхні, наприклад, нікельованого чайника або каструлі. Цікаво спостерігати за зміною свого відображення у звичайній полірованої ложці, якщо повертати її то увігнутою, то опуклою стороною.

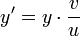
Для вгнутого сферичного дзеркала:

Якщо сферичне дзеркало ввігнуте, можливі різні випадки розташування зображення щодо дзеркала при різних відстанях до предмета. Буквою C позначений центр дзеркала, а буквою F - його фокус. При u > F формула дзеркала має вигляд:

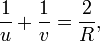
а при u < F:

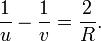
Для побудови взято три промені (хоча достатньо і двох):

· промінь, паралельний головній оптичній осі після відображення від дзеркала пройде через його фокус;

· промінь, що проходить через фокус після відбиття піде паралельно головній оптичній осі;

· промінь, що падає на полюс дзеркала після відбиття піде під кутом, рівним куту падіння (за законом відбиття світла).

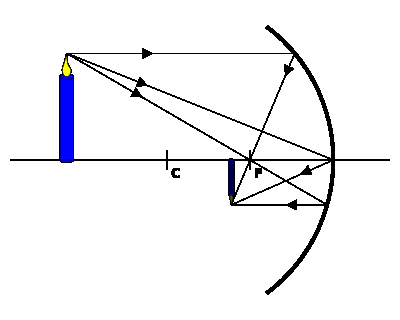
Мал. 11)

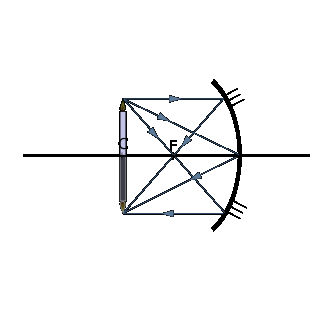
Якщо предмет наближений до дзеркала і знаходиться на відстані, що перевищує відстань від дзеркала до його центру, то зображення його буде дійсним, перевернутим і зменшеним і розташується на відрізку між центром і фокусом (мал.11).

Мал. 12)

Якщо предмет розміщений в центрі дзеркала, то його зображення також буде розташовано в центрі дзеркала. Зображення виходить дійсним, перевернутим і рівним за величиною предмету (мал.12).

Мал. 13)

Якщо предмет поміщений між центром і фокусом, то зображення буде розташовано далі від дзеркала, ніж його центр і буде дійсним, перевернутим і збільшеним (мал.13).

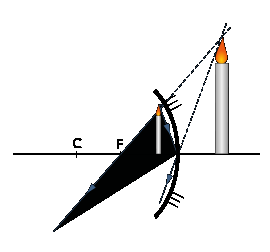
Мал. 14)

Якщо предмет ближче фокусу до дзеркала, то зображення - уявне, пряме, збільшене, по інший бік дзеркала від предмета (мал.14).

Для опуклого сферичного дзеркала:

Побудова зображення в опуклому сферичному дзеркалі простіше, ніж в увігнутому: тут при будь-якій відстані предмета до дзеркала його зображення буде розташовано за дзеркалом. На малюнку нижче буквою F позначений фокус опуклого дзеркала, буквою V - полюс, y - висота предмета, y '- висота зображення. Формула дзеркала в цьому випадку має вигляд:

Для побудови взято два промені:

· промінь від верхньої точки предмета, паралельний головній оптичній осі, відіб'ється від дзеркала, і продовження цього відбитого променя пройде через фокус і через верхню точку зображення;

· промінь від верхньої точки предмета, продовження якого проходить через фокус, після відображення піде паралельно головній оптичній осі, а продовження цього відбитого променя також пройде через верхню точку зображення.

Таким чином, верхньою точкою зображення буде точка перетину продовження першого відбитого променя і продовження другого відбитого променя.

Зображення в опуклому дзеркалі - уявне, пряме, зменшене, знаходиться по інший бік дзеркала від предмета.

Застосування сфериних дзеркал

У житті ви часто бачили своє спотворене відображення на опуклій поверхні, наприклад, нікельованого чайника або каструлі. Цікаво спостерігати за зміною свого відображення у звичайній полірованої ложці, якщо повертати її то увігнутою, опуклою стороною.

В оптичних приладах застосовуються дзеркала з різною відбиваючою поверхнею: плоскі, сферичні і складніших форм. Неплоских дзеркала подібні до лінз, які мають властивість збільшувати або зменшувати зображення предмета в порівнянні з оригіналом.

Дата добавления: 2015-09-03