Прохождение случайных сигналов через линейные устройства

Рассмотрим модель воздействия стационарных случайных сигналов на линейные устройства (рисунок 7). Пусть устройство характеризуется ком­плексным частотным коэффициентом передачи K (j ) и импульсной (весовой) функцией g (t).

Рисунок 7- Случайные сигналы

Ключ К при t <0 разомкнут и в этом случае X (t)=0 и Y (t)=0, т.e. имеем нулевые начальные условия. В момент t = 0 замыкается ключ К и на вход устройства подается стационарный процесс X (t). Начинается переходной режим. В этом режиме на выходе будет нестационарный процесс. Через время t _y устанавливается стационарный режим, при котором Y (t) - стационарный процесс.

Обычно решается следующая типичная задача. Известны математиче­ское ожидание m _1x и корреляционная функция R_x () входного сигнала. Требу­ется найти m _{1 y} и R_y (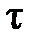) для выходного сигнала. При этом возможны два усло­вия:

1) изучение нестационарного и стационарного режимов;

2) изучение только стационарного режима.

Первое условие.

Здесь для решения задачи при ненулевых начальных ус­ловиях нужно использовать дифференциальные уравнения. Для нулевых ус­ловий следует использовать весовую функцию g (t). Тогда выходной сигнал определяется интегралом свертки

.

Отсюда следует:

1) 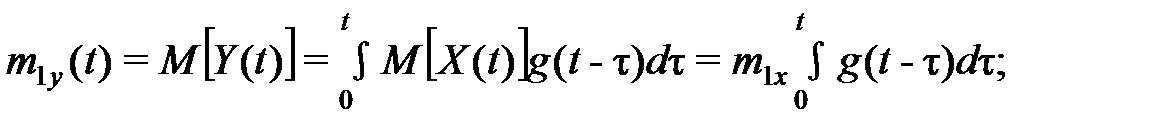(33)

2) . (34)

Стационарное значение функции m _{1 y} (t) будет при t →∞ Стационарное значение функции R (t ₁ t ₂) будет при t ₁→∞ и t ₂→∞, Если последова­тельно сделать замену переменных, а именно сначала ₁= t ₁- x и ₂ = t ₂- у, а затем = t ₂ – t ₁ и z = + х - у, то формула (34) приводится к виду:

.

Отсюда при t₁→∞ следует стационарное значение

. (35)

Второе условие.

Когда интересуются только стационарным режимом, то применяют комплексный коэффициент передачи K (j ), рис.8

Рисунок 8 - Комплексный коэффициент передачи

Спектральная плотность мощности выходного сигнала

S_y ()= S_x ()* K ²(), (36)

где К () - амплитудно-частотная характеристика (АЧХ) устройства. Среднее значение выходного сигнала

m _{1 y} = K (0)* m _{1 x} (37)

Корреляционная функция

(38)

Дисперсия выходного сигнала

. (39)

В заключение следует отметить, что задача определения плотности ве­роятности выходного сигнала в общем виде не решается. В частном случае, когда X (t) - нормальный процесс, выходной сигнал Y (t) также является нор­мальным процессом.

Контрольные вопросы:

1 Какие бывают режимы работы линейных устройств.

2 Какие бывают частотные характеристики.

3 Что такое передаточная функция.

4 Какие бывают временные характеристики.

5 Что такое переходная функция.

6 Объяснить смысл преобразований Фурье и Лапласа.

7 Какие бывают методы определения выходного сигнала при заданных входном сигнале и характеристиках устройства.

8 Объяснить смысл термина динамическая погрешность преобразования.

9 Какие бывают энергетические характеристики выходного сигнала.

10 Как происходит коррекция динамических характеристик устройства.

11 Что такое ком­плексный частотный коэффициент передачи.

12 Что такое импульсная (весовая) функция.

13 Объяснить смысл термина математиче­ское ожидание.

14 Объяснить смысл термина корреляционная функция.

15 Что такое амплитудно-частотная характеристика.

16 Что такое фазо-частотная характеристика.

17 Что такое амплитудно-фазовая частотная характеристика.

18 Объяснить смысл термина дисперсия выходного сигнала.

19 Что такое спектральная плотность мощности выходного сигнала.

20 Рассказать принцип работы масштабирующего устройства (датчика).

Дата добавления: 2015-10-31