
Читайте также:
|
Качество работы реального устройства в динамическом режиме оценивается динамической погрешностью, которая обычно устанавливается путем сопоставления результатов преобразования входного сигнала для идеального и реального устройства. Под динамической погрешностью во временной области понимают разность откликов реального и идеального ЛУ, т.е.
Δ(t) = у реал (t) - у идеал (t). (23)
Динамическую погрешность можно определить и в частотной области как преобразование Фурье функции Δ(t), а именно
Р Δ(j  ) = [ к (j
) = [ к (j  )- К ид(j
)- К ид(j  )] F x(j
)] F x(j  ) или Δ(р) = [ K (р)- к ид(р)] X (р), (24)
) или Δ(р) = [ K (р)- к ид(р)] X (р), (24)
где K (j  ) и К ид(j
) и К ид(j  ) - комплексные частотные коэффициенты передачи соответственно реального и идеального устройств. При этом
) - комплексные частотные коэффициенты передачи соответственно реального и идеального устройств. При этом
A (t) = 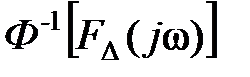 .
.
Отсюда следует, что динамическая погрешность зависит как от характеристик устройства, так и от вида входного сигнала.
Вид комплексного коэффициента передачи идеального устройства зависит от характера его преобразования (масштабирование, дифференцирование, интегрирование и т.д.) и от формулировки требований, предъявляемых к операции преобразования.
В технике наиболее распространенной операцией является масштабирование. Масштабирующее устройство (датчик) должно обеспечивать неискажаемую передачу входного сигнала. Для этого достаточно, чтобы отклик был точной копией входного сигнала. При этом допускается различие в амплитуде, так как важна форма, а не величина отклика. Кроме того, часто допускается запаздывание во времени выходного сигнала относительно воздействия.
Поэтому можно считать, что сигнал x(t) передается без искажений, если отклик устройства y(t) = К*x(t – t0), где К - масштабный коэффициент, равный частотному коэффициенту передачи К(0) на нулевой частоте, и t0 - время запаздывания. На основании свойства временного сдвига преобразования Фурье имеем
Fy (j  ) = Кид (j
) = Кид (j  ) Fx (j
) Fx (j  ) = K (0) Fx (j
) = K (0) Fx (j  ) e-j
) e-j  t0.
t0.
Следовательно, при масштабировании идеальное (неискажающее) устройство должно иметь комплексный коэффициент передачи
К ид(j  ) = К ид(
) = К ид( )*
)* 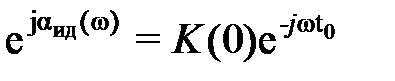 . (25)
. (25)
Отсюда следует, что АЧХ такого устройства должна быть постоянна на всех частотах и равна К (0), т.е. К ид( ) = К (0). С другой стороны, ФЧХ должна быть линейной функцией частоты, т.е. а ид(
) = К (0). С другой стороны, ФЧХ должна быть линейной функцией частоты, т.е. а ид( ) = -
) = -  * t 0. Если запаздывание выходного сигнала недопустимо, то ФЧХ а ид (
* t 0. Если запаздывание выходного сигнала недопустимо, то ФЧХ а ид ( ) = 0.
) = 0.
2.5 Определение энергетических характеристик выходного сигнала
Задача определения энергетических характеристик выходного сигнала решается на основании теоремы Парсеваля и понятия энергетических характеристик в частотной области. В результате на выходе имеем:
а) спектральную плотность энергии
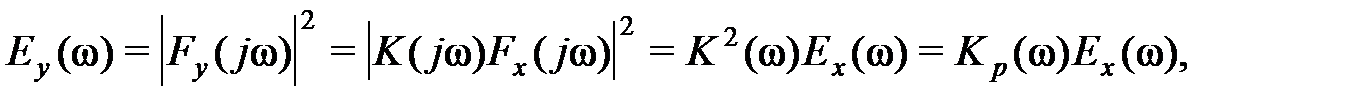 (26)
(26)
где Е ( )- спектральная плотность энергии входного сигнала,
)- спектральная плотность энергии входного сигнала,
Ех ( ) = |Fx(j
) = |Fx(j  )|2 =
)|2 = 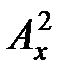 (
( ), и Кр (
), и Кр ( ) = | K (j
) = | K (j  )|2 = К 2(
)|2 = К 2( ) - частотный коэффициент передачи мощности;
) - частотный коэффициент передачи мощности;
б) энергию
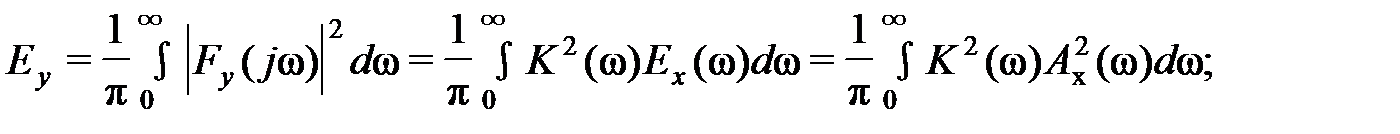 (27)
(27)
в) спектр плотности мощности
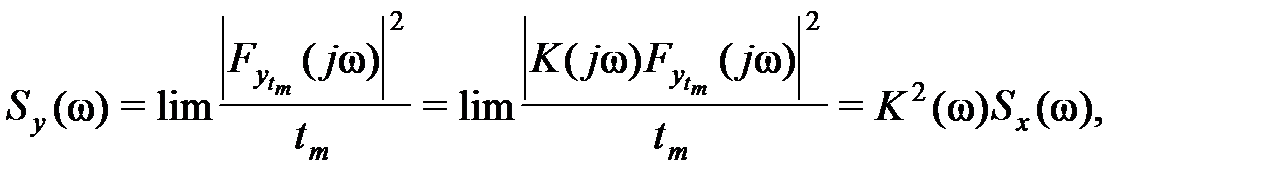 (28)
(28)
где Sx ( ) - спектральная плотность мощности входного сигнала;
) - спектральная плотность мощности входного сигнала;
г) среднюю мощность
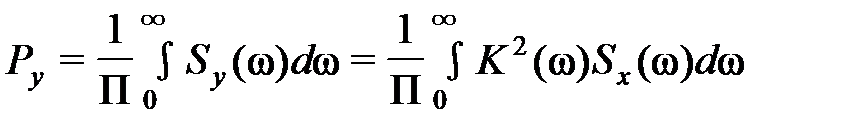 . (29)
. (29)
Для периодических сигналов формула (3.29) с учетом (1.10) приводится к виду
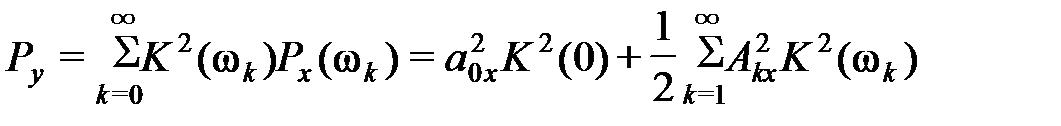 . (30)
. (30)
Дата добавления: 2015-10-31; просмотров: 111 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Временные характеристики. | | | ПРОХОЖДЕНИЕ СЛУЧАЙНЫХ СИГНАЛОВ ЧЕРЕЗ ЛИНЕЙНЫЕ УСТРОЙСТВА |