Временные характеристики.

Весовая или импульсная функции g (t), t >0 ⎯ это реакция (или отклик) устройства на дельта-функцию δ(t) или функцию Дирака Dirac(t) для Mathcad (рис. 3). Для физически реализуемых устройств g (t)=0 при t <0.

Рисунок 3- Импульсная функция

Эта функция связана простым соотношением с комплексным коэффициентом передачи К (j ω), именно

g (t)= (4)

или в операторной форме (обратное преобразование Лапласа)

g (t) (5)

Зная в результате эксперимента весовую функцию g (t), можно определять или комплексный коэффициент передачи К(jω) или передаточную функцию К (р):

(6)

Переходная функция h (t), t >0 - это реакция устройства на единичную функцию l (t) или функцию Хевисайда ȹ(t) для Mathcad (рис.4). Для физи­чески реализуемых устройств h (t)=0 при t <0.

Рисунок 4-Переходная функция

Связь между функциями h (t) и K (j ) определяется выражением

h (t)= . (7)

Если учитывать только переменную (~) составляющую отклика (постоянной составляющей К (0)/2 пренебрегаем), то тогда связь между функциями h (t), K (j ) и К (р) принимает вид

h (t)= . (8)

h (t)= . (8a)

. (9)

K (p)= 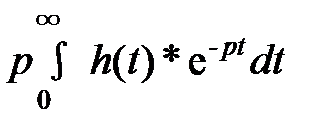. (9a)

Примечания

1 Вычисление интегральных преобразований Фурье и Лапласа.

Это вычисление значительно облегчается при использовании методов контурного интегрирования на плоскости комплексного переменного Вычеты и контурные интегралы.

Пусть f (z) есть функция комплексной переменной z = x + jy. Пусть эта ком­плексная функция аналитична в точке z = a, т.е. дифференцируема в некоторой окрестности точки а. Корни уравнения f (z)=0 называют нулями функции f (z). Нулю порядка m соответствует m одинаковых корней уравнения f (z)=0.

Точка z = a является особой, если в самой точке z = a функция f (z) неаналитична, а в ее окрестностях - аналитична. К особым точкам относятся полю­са f (z). Точка z = a является полюсом, если lim f (z) = ∞. Точка z = a будет полюсом порядка r, если комплексную функцию можно представить в виде

f (z)= , где аналитична и 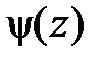0

Вычетом Re s f (a) функции f (z) в точке z = a называется контурный инте­грал вида

Re s f (a)= ,

где С -контур, окружающий точку z = a. Стрелка показывает, что интеграл берется по пути С в направлении против часовой стрелки. Тогда интегриро­вание ведется внутри контура С и вычитается эта область.

При z =∞ вычет

Re s f (a)= ,

где интегрирование проводится по часовой стрелке и соответствует области вне контура С. Следует отметить, что Re s f (∞) = lim [- zf (z)].

Есди z = a ∞ есть полюс порядка r, то вычет

Re s f (a)= (10)

В частности, если z = a ∞ - простой полюс (r =1) и f (z)= M (z)/ N (z), где M (z) и N (z) - аналитические функции в точке z = a, причем M (a) 0, N (a)=0 и N '(a) 0, то вычет

Re s f (a) = . (11)

Вычислить интеграл по замкнутому контуру, охватывающему особые точки z ₁ z ₂,.., z _n, позволяет теорема о вычетах

Или в другой форме:

(12)

Теорема вычетов позволяет также находить некоторые определенные интегралы от функций действительной переменной t вида:

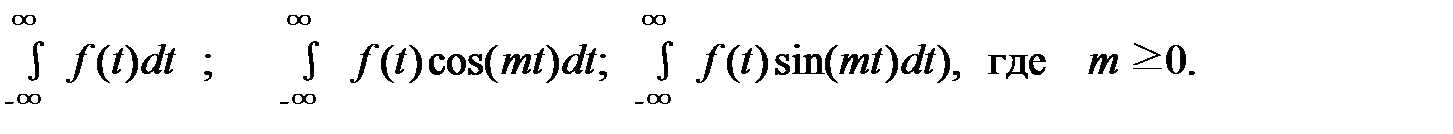
Для их вычисления следует применить формулу (12) к контуру, состоящему из интервала (- R, R) действительной оси и дуги C_r окружности | z |= R в верх­ней полуплоскости. При R →∞, согласно леммы Жордана, можно отбросить интегралы по дуге C_R.

Например, если при замене действительной переменной t на комплекс­ную переменную z функция f (z) аналитична в верхней полуплоскости с уче­том действительной оси, за исключением конечного числа особых точек z_{k :}, лежащих сверху от действительной оси, и уравнение f(l/ z)=0 имеет нулевые корни кратности m 2, то

(13)

2 Вычисление обратного преобразования Лапласа.

Если F (p) - алгебраическая функция и выражается отношением двух многочленов F (p)= M (p)/ N (p), причем степень многочлена М (р) выше степени многочлена N (p), то обратное преобразование L ^-1[ F (p)] равно сумме вычетов функции F (p) -e ^pt по всем особым точкам (полюсам) функции F (p).

Для вычисления обратного преобразования Лапласа сначала находят корни р _к уравнения N (p)=0, которые определяют полюсы F (p). Если корни уравнения простые (z =1), то N (p)= a ₀(p - p ₁)(p - p ₂)…(p - p_n) и обратное преобразо­вание

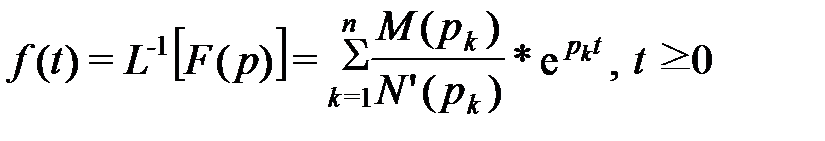(формула обращения). (14)

Дата добавления: 2015-10-31