Методы расчета константы равновесия

Расчётные методы определения константы равновесия реакции обычно сводятся к вычислению тем или иным способом стандартного изменения энергии Гиббса в ходе реакции (ΔG⁰), а затем использованию формулы:

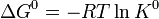
При этом следует помнить, что энергия Гиббса — функция состояния системы, то есть она не зависит от пути процесса, от механизма реакции, а определяется лишь начальным и конечным состояниями системы. Следовательно, если непосредственное определение или расчёт ΔG⁰ для некоторой реакции по каким-либо причинам затруднены, можно подобрать такие промежуточные реакции, для которых ΔG⁰ известно или может быть легко определено, и суммирование которых даст рассматриваемую реакцию (см. Закон Гесса). В частности, в качестве таких промежуточных реакций часто используют реакции образования соединений из элементов.

Энтропийный расчёт изменения энергии Гиббса и константы равновесия реакции

Энтропийный метод расчёта ΔG реакции является одним из самых распространённых и удобных^[2]. Он основан на соотношении:

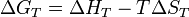
или, соответственно, для стандартного изменения энергии Гиббса:

Здесь ΔH⁰ при постоянных давлении и температуре равно тепловому эффекту реакции, методы расчёта и экспериментального определения которого известны — см., например, уравнение Кирхгофа:

Необходимо получить изменение энтропии в ходе реакции. Эта задача может быть решена несколькими способами, например:

По термическим данным — с опорой на тепловую теорему Нернста и с использованием сведений о температурной зависимости теплоёмкости участников реакции. Например, для веществ, при нормальных условиях находящихся в твёрдом состоянии:

где S₀ = 0 (постулат Планка) и тогда, соответственно,

.

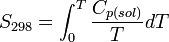(здесь индекс sol — от англ. solid). При некоторой заданной температуре T:

Для жидких или газообразных при нормальной температуре веществ, или, в более общем случае, для веществ, в интервале температур от 0 (или 298) и до T претерпевающих фазовый переход, следует учитывать изменение энтропии, связанное с этим фазовым переходом.

Для идеальных газов — методами квантовой статистики.

Различными эмпирическими и полуэмпирическими методами, для этого часто достаточно небольшого объёма исходных данных. Например, для твёрдых неорганических веществ оценить энтропию можно по формуле

где A и B — табличные константы, зависящие от типа рассматриваемого соединения, M — молекулярная масса.

Итак, если извеcтны , 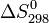и температурные зависимости теплоёмкости, может быть рассчитано по формуле:

Несколько упрощённый вариант этой формулы получают, считая сумму теплоёмкостей веществ не зависящей от температуры и равной сумме теплоёмкостей при 298 K:

И еще более упрощённый расчёт проводят, приравнивая сумму теплоёмкостей к нулю:

Переход от к константе равновесия осуществляется по приведённой выше формуле.

Принцип Ле Шателье — Брауна (1884 г.) — если на систему, находящуюся в устойчивом равновесии, воздействовать извне, изменяя какое-либо из условий равновесия (температура, давление, концентрация), то в системе усиливаются процессы, направленные на компенсацию внешнего воздействия.

Анри Ле Шателье (Франция) сформулировал этот термодинамический принцип подвижного равновесия, позже обобщённый Карлом Брауном

Дата добавления: 2015-10-23