
|
Читайте также: |
Механическое движение как простейшая форма
Движения материи
При механическом движении происходит перемещение одних тел относительно других. Если имеется одно единственное тело, то говорить о его перемещении бессмысленно. Поэтому одно из тел (или группу тел неподвижных относительно друг друга) выбирают в качестве системы отсчёта. В отсутствии тел нельзя себе представить пространство. Пространство и время это формы существования материи. Понятия пространства, его геометрических элементов (точка, линия, поверхность, объём) возникли как абстракция свойств материальных тел.
В механике Ньютона считается, что пространство однородно во всех своих частях и изотропно, т.е. его свойства не зависят от направления. Иначе говоря, предполагается, что физическое пространство такое же, каким его представляет геометрия Евклида. Для классической механики, механики малых по сравнению со скоростью света скоростей, это допущение вполне приемлемо. Но представление о существовании абсолютно неподвижного пространства неверно. Пространство мы всегда мыслим связанным с определёнными телами, телами отсчёта.
По Ньютону время это абсолютная длительность, существующая независимо от тел. Т.е. время течёт во всех точках пространства одинаково. Это трудно обосновать. Длительность неотделима от материи, поскольку время есть форма существования материи. Время связано с движением тел и зависит от скорости. В рамках одной системы отсчёта можно установить одну меру длительности для всех процессов и явлений. Тогда можно утверждать, что существует одно единое время. Но течение времени связано с относительным движением систем отсчёта, т.е. нет единого абсолютного времени для всех систем отсчёта. Длительность процессов связана с движением, понятие времени неотделимо от движения тел относительно друг друга.
При медленных относительных движениях, когда скорость очень мала по сравнению со скоростью света, зависимость времени от относительного движения системы отсчёта практически ничтожна, и ею можно пренебречь. Поэтому в классической механике можно считать вполне допустимыми представления Ньютона об абсолютном и едином времени.
Элементы кинематики материальной точки
Раздел механики, в котором рассматриваются только методы описания движений, но не ставятся вопросы о законах движения, называется кинематикой.
Нормальное и тангенциальное ускорения
В произвольном случае движения скорость не остаётся постоянной.
Быстрота изменения скорости по величине и направлению характеризуется ускорением. Это величина векторная.
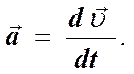
Рассмотрим произвольный малый участок траектории.
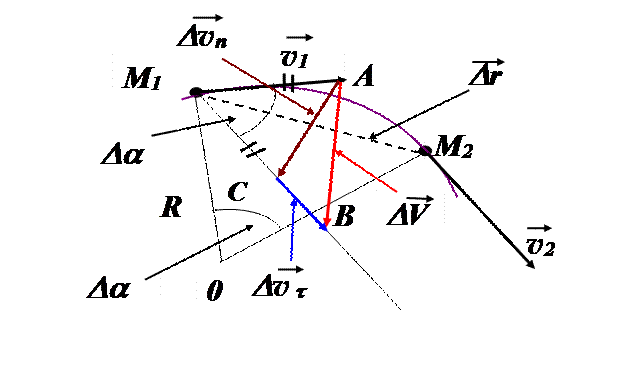
Проведём участок траектории М1М2. В точках М1 и М2 проведём вектора скоростей v 1 и v2 касательные к траектории. Из точки М1 проведём прямую параллельную вектору скорости v2. Отложим на этой прямой отрезок М1С, равный по модулю v1. Отрезок СВ равен по модулю изменению скорости. В общем случае изменение скорости будет равно.
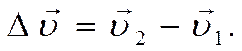
Среднее ускорение 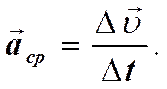
Мгновенное ускорение 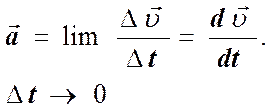 (1)
(1)
С другой стороны изменение скорости 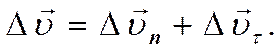 При этом
При этом 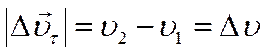 и характеризует изменение численного значения (модуля) скорости. Вектор
и характеризует изменение численного значения (модуля) скорости. Вектор 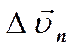 характеризует изменение скорости по направлению. Он направлен в сторону вогнутости кривой. Из выражения (1) следует, что
характеризует изменение скорости по направлению. Он направлен в сторону вогнутости кривой. Из выражения (1) следует, что
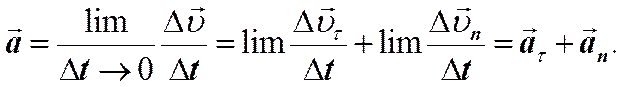 (2)
(2)
Здесь at – тангенциальное ускорение, an – нормальное ускорение.
При Dt®0 угол Da®0 направление векторов v2 и Dv t стремятся к направлению вектора v1. Поэтому вектор, аt направлен по касательной к траектории и его численное значение характеризует быстроту изменения скорости по величине.
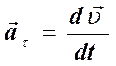 и называется тангенциальным ускорением.
и называется тангенциальным ускорением.
Для нахождения нормального ускорения an восстановим в точках М1 и М2 перпендикуляры к траектории (к касательным в данных точках, т.е. к соответствующим скоростям). Эти перпендикуляру называются нормалями. Нормали пересекутся в точке О. Так как мы выбрали малый промежуток времени Dt, то отрезок траектории М1М2 есть отрезок окружности с центром в точке О и радиусом R» ОМ1 » ОМ2. Угол между ОМ1 и ОМ2 равен Da.. Если DS = М1М2 – дуга, то
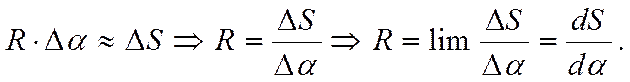
R – радиус кривизны траектории. Величина обратная радиусу кривизны называется кривизной. 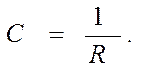
На рисунке имеется два равнобедренных треугольника D М1М2О и D АСМ1. Из их подобия следует.
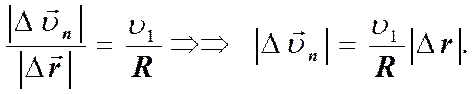 Отсюда вычислим величину искомого вектора an.
Отсюда вычислим величину искомого вектора an.
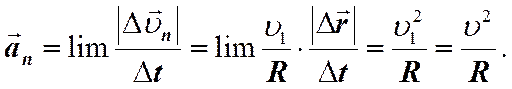
В пределе угол Da ® 0 и вектор Dvn ^ v1. Следовательно, вектор an также будет перпендикулярен вектору v1, т.е. вектору скорости. Вектор an направлен по нормали к траектории и называется нормальным ускорением. Таким образом, полное ускорение будет равно.
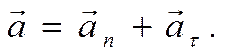 Причём вектора an ^ at.
Причём вектора an ^ at.
Для равномерного движения точки по окружности at = 0, R = const и нормальное ускорение будет постоянным по величине и направлено к центру окружности. Оно еще называется центростремительным ускорением.
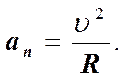
При неравномерном прямолинейном движении R =¥, а an = 0.
Рассмотрим движение тела брошенного горизонтально.
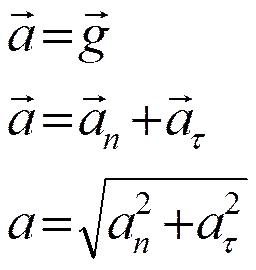
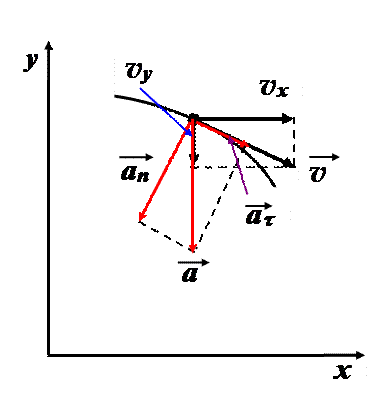
Кинематика твёрдого тела. Теория движения твёрдого тела играет важную роль, так как на практике мы всегда имеем дело с телами, а не с точками. Поэтому различают два основных вида движения: поступательное и вращательное. Все виды механического движения могут быть сведены к совокупности этих движений.
Поступательное движение. Это такое движение, при котором любая прямая, связанная с телом, остаётся параллельной самой себе, а все точки тела совершают одинаковые перемещения за одинаковые промежутки времени. Поэтому скорости и ускорения всех точек тела одинаковы. Это позволяет свести изучение поступательного движения твёрдого тела к изучению движения отдельной точки тела, т.е. к задаче кинематики материальной точки.
Дата добавления: 2015-10-31; просмотров: 110 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
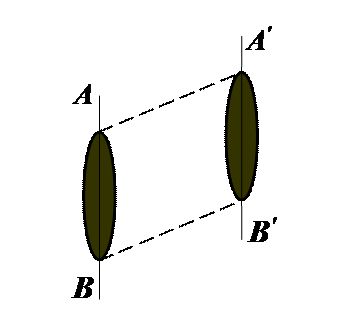
| ВНИМАНИЕ! Фамилии, имена и названия организаций выполняются только на английском языке! | | | Движение твёрдого тела, при котором все точки тела движутся по окружностям, центры которых лежат на одной прямой называется вращением тела вокруг неподвижной оси. |