Движение твёрдого тела, при котором все точки тела движутся по окружностям, центры которых лежат на одной прямой называется вращением тела вокруг неподвижной оси.

Пусть абсолютно твёрдое тело вращается вокруг неподвижной оси ОО'. Проследим за некоторой точкой М этого тела.

За время dt точка М совершает перемещение dr. При этом же угле поворота dj другая точка, отстоящая на большее расстояние от оси совершит другое (большее) перемещение. Поэтому использовать перемещение dr любой точки твёрдого тела неудобно для характеристики вращения всего тела.

За время dt любая плоскость, связанная с твёрдым телом и проходящая через ось вращения, повернётся на угол dj, или, что тоже самое, на угол dj повернётся радиус-вектор R точки М, перпендикулярный оси вращения. Угол dj служит характеристикой вращения всего твёрдого тела. Удобно ввести вектор dj поворота тела, численно равный dj и направленный вдоль оси вращении ОО' так, чтобы, глядя по направлению вектора dj, мы видели вращение по часовой стрелке. Направление вектора dj и направление вращения связаны правилом правого винта.

Для характеристики быстроты вращения вводят вектор угловой скорости.

Вектора w и dj направлены в одну сторону.

Если w = const, то вращение является равномерным.

Рассмотрим связь между линейной скоростью точки М (V) и её угловой скоростью w.

За время dt точка М проходит путь.

Таким образом Из рисунка видно, что вектора v ^ w и v ^ R, т.е. вектор v есть векторное произведение.

Или в скалярной форме. Причём

Наряду с угловой скоростью используются понятия периода Т и частоты вращения v.

Период Т – это промежуток времени, течение которого тело совершает полный оборот, т.е. поворот на угол j = 2p. Частота v это число оборотов за 1 секунду. При вращении с угловой скоростью w она будет равна.

Угловое ускорение.

Угловое ускорение вводится для характеристики неравномерного вращения тела. Угловое ускорение является вектором.

Вектор углового ускорения e направлен в ту же сторону, что и вектор w при ускоренном вращении и в противоположную сторону при замедленном вращении .

Рассмотрим связь между угловым и линейным ускорением точки М. Линейное ускорение разлагается на два ускорения: нормальное (a_n) и тангенциальное (a_t).

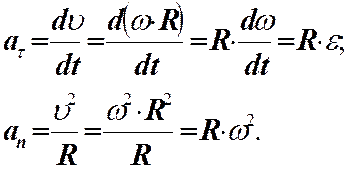
Дата добавления: 2015-10-31