Круг, кольцо, цилиндр, труба и конус, шары и купола

Появление такого параметра, как полярность, дало возможность заглянуть и в другие тайники природы. Представляем беглый обзор новых данных о свойствах давно известных форм в свете новой реальности, полученной при общении с информационным полем средствами биолокации.

Относительно полярности контура круга можно ответить коротко — ее нет. Следовательно, это какая-то фундаментальная гармоничная фигура. Другое дело — статическая информационная структура от символа или контура. Такая структура есть, она нами изучается, и результаты будут опубликованы в следующей работе. В новой реальности мы уже столкнулись с подобными явлениями. Пирамида Хеопса тоже не полярна, но создает наиболее мощную информационную структуру. Полярность дает информацию о типах форм, на которые раскладываются все формы в новой реальности.

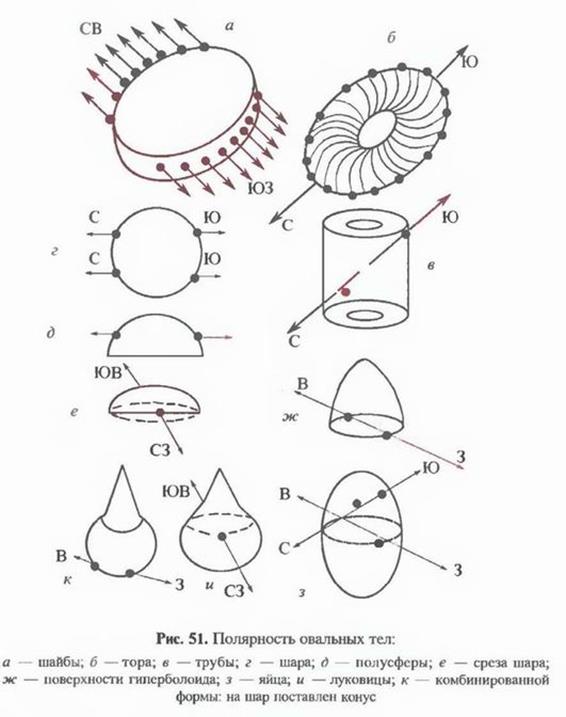
Как только у круга появляется объем, то есть появляется форма диска, появляется и полярность по линии СВ-ЮЗ, где «плюс» на юго-западе, а расположение точек полярности на середине высоты (рис. 51а). Видим, что при соотношении диаметра шайбы к толщине как 5,5:1 шайба поделилась на 8 объемов. Составляем известный нам столбик:

5,5

х0,6 деление на 2

3,3

xQ,6 деление на 3

1,98

xQ,6 деление на 5

1,188

х0,6 деление на 8

0,8

Мы достигли величины высоты шайбы и даже получили несколько меньшее значение.

Как видим, эксперимент подтвердил деление на 8 частей. Следуя уже сложившейся логике, цилиндр с соотношением диаметра к высоте 1:0,6 должен быть гармоничным, то есть не обладать полярностью, что и подтвердилось экспериментально. Второй гармоничный цилиндр будет обладать соотношением высоты к диаметру как 1:0,6. Точно так же как у пирамид с египетской и суданской геометрией. При изучении круглых карандашей и кусков толстой проволоки еще раз наблюдаем закономерное деление объемов по вертикали, а при длинной проволоке с трудом наблюдаем цепочку сигналов на поверхности по всей длине, которая при большой длине просто исчезает. В силу вступают иные закономерности, которые мы осветим в следующей публикации.

Полярность кольца — тора С-Ю, где «плюс» на севере. Тор в форме диска с величиной диаметра отверстия 5 мм и внешнего диаметра диска 30 мм. Если составить привычный столбик, то получим количество объемов, на которые разобьется диск, равное восьми. Эго же подтвердил эксперимент.

Полярность трубы также оказалась по линии С-Ю, где «плюс» на севере. При малом центральном отверстии и большой длине количество делений как по горизонтали, так и по вертикали возрастает, а амплитуда сигнала падает. Форма постепенно переходит в разряд цельного цилиндра. Точки полярности в обоих случаях находятся на середине высоты.

Полярность конусов оказалась точно такой же, как у пирамид, то есть по линии 3-В, причем точки полярности находятся на уровне основания. Знаки полярности те же, то есть на западе — «минус».

Магический угол 51° у конусов проявился особенно ярко, поскольку нет игры углов в гранях и сечениях, как в пирамидах. Также обнаружены несколько зон магических углов, которые едины с пирамидальными и треугольными формами. Наблюдаются те же деления объемов по горизонтали, если углы наклона стенки конуса становятся острее 51°, и деление по вертикали, если углы становятся тупее 51°. Есть ещ£ ряд зон углов, когда конуса перестают быть полярными.

При делении по вертикали конуса делятся не на равные части, а с убыванием. Высота нижней секции больше последующей в 1,4 раза, так же, как у пирамид.

Особенно удивила нас полярность шаров. Оказалось, что у шара две оси полярности, проходящих через центры обоих полушарий. Знаки полярности — «плюс» на севере, «минус» на юге (см. рис. 51г). Ни о каких делениях и магических углах здесь речь не идет. Но самое главное в том, что шар оказывается, не является законченной гармоничной фигурой. Отдельно взятое полушарие, как показано на рис. 5Id, обладает такой же полярностью, как и в составе шара. Та же самая картина будет, если полушарие перевернуть. Если рассмотреть объем, представляющий собой срез шара менее чем по диаметру, то получим совершенно другую картину распределения полярности. Точки полярности разместятся на линии СЗ-ЮВ, причем «плюс» окажется на СЗ (рис. 51<?). Видимо, все это учитывалось при постройке куполов церквей, особенно внутренних. Найти полную полусферу во внутренних помещениях храмов нам не удалось. Везде мы наблюдали срезы, но не полусферы.

Фигура, которая часто встречается в куполах, — это гиперболоид, напоминающий раздутый конус, который имеет полярность конуса. Это «минус» на западе в основании фигуры.

Как и шар, яйцо не оказалось фигурой гармоничной или скорее единичной (начальной и тому подобное). Яйцо состоит из двух форм с разнонаправленной полярностью, как показано на рис. 51з. Разделенные половинки яйца показали ту же картину. Объем яйца с острого конца соответствует предыдущему гиперболоиду или раздутому конусу, а половинка яйца с тупого конца соответствует полусфере.

Совершенно особую полярность имеет форма луковицы, как показано на рис. 51 и. Точки впервые расположились по оси СЗ-ЮВ, причем в середине объема, «плюс» оказался на СЗ.

Мы попробовали смоделировать форму наверший православных храмов и поставили конус на шар, как показано на рис. 51 ас. Получили какую-то неправдоподобную картину. Полярность вроде бы напоминает полярность конуса, где «минус» на западе оказался также внизу фигуры. Другими словами, у нас не получилось смоделировать знаменитую церковную луковицу.

 

Полученная нами новая информация о каких-то фундаментальных различиях в типах форм относится к разряду сюрпризов новой реальности. Мы опять напоминаем читателю, что эти сюрпризы еще не закончились, многие из них уже оказались полезными и находят логическое объяснение и даже практическое подтверждение.

Дата добавления: 2015-10-30