Постановка вопросов в процессе проблемного обучения

Под проблемным обучением понимается такое изучение мате­риала, которое вызывает в сознании учащихся познавательные задачи и проблемы, напоминающие научный поиск³. Разрешение этих проблем активизирует творческие умственные способности учащихся.

В младших классах проблемные ситуации возникают при формулировании загадок, задач на сообразительность и смекал­ку, шарад. Такие проблемные ситуации можно создавать, пред­лагая детям обобщить чувственные данные и сделать вывод. Можно, например, поставить вопрос: «Почему лед, пар, облака называют водой?» Другим примером проблемной ситуации для учащихся младших классов является постановка задачи: постро­ить треугольник по трем заданным углам [специально даются такие углы, сумма которых значительно больше (или меньше) 180°]. Учащиеся не могут выполнить эту задачу и думают над причиной, почему она неразрешима.

В начальных классах перед учащимися можно ставить пробле­мы, направленные на поиски математических закономерностей: 1) изменение суммы в зависимости от изменения одного из сла­гаемых; 2) изменение частного в зависимости от изменения дели­мого или делителя; 3) изменение площади квадрата в зависимо­сти от увеличения или уменьшения в несколько раз его стороны и т. д. Эффективны и отдельные проблемные вопросы типа: «Почему четырехугольник назван четырехугольником? Можно ли было дать ему другое название, также связанное с его свой­ством?» или «Как бы вы назвали треугольник, у которого один угол тупой?»⁴ Учитель в процессе ответа на основной проблем­ный вопрос должен уметь ставить и наводящие вопросы. В процессе обучения математике возникают различные типы задач (стандартная обучающая, поисковая, проблемная). Основ­ными компонентами задачи считают: условие, заключение, реше­ние, обоснование решения, которые могут быть не известны человеку (в частности, школьнику) в момент постановки перед ним данной задачи. Стандартная задача — это такая задача, у которой четко определено условие, известен способ решения и его обоснование и которая представляет собой упражнение на воспроизведение известного. Обучающей является та задача, в ко­торой неизвестен (или плохо определен) один из вышеуказанных основных компонентов. Если неизвестны какие-либо два компо­нента, то задачу называют поисковой, а три — проблемной⁵.

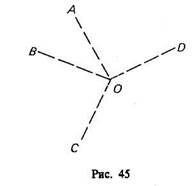
Это деление задач несколько условно, так как в зависимости от уровня знаний и методической подготовки человека она может быть отнесена к тому или иному типу. Например, при изучении темы «Вписанные четырехугольники» учитель ставит перед уча­щимися такую вводную задачу (проблему): «Где расположить центральный штаб туристского слета, чтобы он находился на равных расстояниях от заданных мест расположения четырех туристских групп?»

Точками А, В, С, D обозначены места расположения групп, а точкой О — предполагаемое место расположения штаба (рис. 45).

В старших классах школьники в процессе проблемного обуче­ния строят различные гипотезы, намечают способы проверки их истинности, самостоятельно «открывают» правила, законы, формулы, доказывают теоремы.

Общая учебная проблема включает в себя несколько частных учебных проблем. Результаты их решения в своей совокупности позволяют дать окончательное решение общей (главной) пробле­мы. Проблемное обучение включает в себя не только создание проблемной ситуации (постановку проблемного вопроса), но и самостоятельную творческую работу учащихся, открытие но­вых для них закономерностей, свойств, отношений, а также логическое обоснование (доказательство) истинности своих суждений и правильности хода рассуждений при опровержении ложных суждений и неправильных умозаключений. Разумеется, проблем­ный метод обучения нельзя превращать в универсальный; его надо использовать наряду с объяснительным, сообщающим из­ложением материала учителем.

Дата добавления: 2015-10-30