Непрямые (косвенные) выводы

К ним относятся: рассуждение по правилу введения имплика­ции; сведение «к абсурду»; рассуждение «от противного» (проти­воречащего).

1. Рассуждение по правилу введения импликации.

Правило вывода сформулировано так:

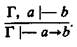
Данное правило читается так: «Если из посылок гамма (Г) и посылки а выводится заключение b, то из одних посылок Г выводится, что а имплицирует b». Это правило вывода имеет и другое название: «Теорема о дедукции». Здесь «Г» может быть и пустым множеством посылок.

Приведем пример рассуждения студента, поясняющий приве­денное правило. Пусть Г содержит следующие посылки: 1) «Я сдал экзамен по педагогике на «отлично»; 2) «Я сдал экзамен по логике на «отлично»; 3) «Я сдал экзамен по математике на отлично». Посылка а означает: «Я успешно выполнил всю порученную мне работу на факультете». Заключение b означает: «Я получу повышенную стипендию». То, что записано над чертой, будет содержательно прочитано так: «Если я сдал экзамены по педагогике, логике и математике на «отлично» и успешно выполнил всю порученную мне работу на факультете, то из этого последует заключение: «Я получу повышенную стипендию». То, что записано под чертой, содержательно можно прочитать так: Я сдал экзамены по педагогике, логике и математике на «отлич­но». Отсюда следует заключение: «Если я успешно выполню всю порученную мне работу на факультете, то я получу повышенную стипендию».

2. Правило сведения к абсурду. Это правило иначе называется правилом введения отрицания.

Правило читается так: «Если из посылок Г и посылки а выво­дится противоречие, т. е. b и не-b, то из одних Г выводится не-а». Метод сведения к абсурду широко применяется в мышлении, как научном, так и в полемическом и в обыденном.

В классической двузначной логике метод сведения к абсурду выражается в виде формулы:— противоречие или ложь.

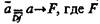
Эта формула говорит о том, что суждение а надо отрицать (считать ложным), если из а вытекает противоречие.

Определение отрицания посредством сведения к абсурду, про­тиворечию широко используется не только в классической, но ив неклассических логиках: в многозначных, конструктивных и интуиционистской.

3. Правило непрямого вывода — рассуждение «от противно­го» (противоречащего). Доказательство «от противного» приме­няется тогда, когда нет аргументов для прямого доказательства. Методом «от противного» нередко доказываются математичес­кие теоремы.

Суть рассуждения «от противного» подробно будет показана в теме «Доказательство», в разделе «Косвенное доказательство».

Итак, мы рассмотрели правила прямых и непрямых (косвен­ных) выводов и убедились, что они широко применяются в мыш­лении. При этом было показано, как та или иная форма прямого или косвенного вывода наполняется конкретным содержанием, взятым из областей педагогики, математики, физики, этики и других областей науки и обыденного мышления, а также из опыта преподавания в средней школе.

Дата добавления: 2015-10-30