Задача потребителя .

Вид. Функция Кобба – Дугласа.

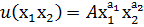
3 вид. Взаимодополняемые товары.

;…

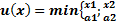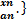
7. Бюджетное множество и бюджетная линия. Задача потребительского выбора. Математическая постановка.

Бюджетным множеством называется множество товаров таких что

=

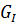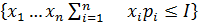
Бюджетной линией называется

=

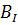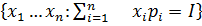
X1p1+x2p2=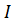

Задача потребителя.

Среди множества товаров доступных потребителю, потребитель стремится выбрать тот, который обеспечит ему наибольший уровень полезности.

Математическая постановка:

U(x1,…xn) -> max

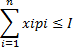
8. Свойства решения задачи потребительского выбора.

1. Решения задач потребительского выбора не должно изменяться при любом монотонном преобразовании функции полезности потребителя: Монотонные преобразования: 1. Умножение функции полезности на положительное число. 2. Логарифмирование по основанию больше 1. 3. Возведение функции в положительную степень.

2. Решение задач потребительского выбора не должно изменяться при увеличении в одинаковой пропорции всех цен товаров и потребителя.

3. Всегда находится на границе бюджетного множества, т.е. на бюджетной линии.

9. Геометрическая иллюстрация решения задач потребительского выбора.

10. Аналитическое решение задачи потребительского выбора. Функция лагранжа. Условие первого порядка. Функция спроса маршала. Экономический смысл множителя Лагранжа.

U(x1,…xn) -> max

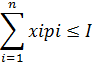
L(x1…xn,λ)=u(x1…xn)-λ(∑xipi- )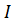

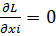
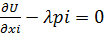
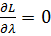∑xipi-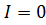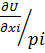

λ= -> λ= -> = =>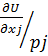

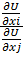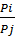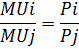
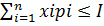- Функция спроса Маршала(зависит от цен и дохода)

11. Модель Стоуна.

Будем предполагать, что определенное количество каждого вида товара необходимо потребителю и вопрос относительно их приобретения не является предметом выбора.

Будем предполагать что функция полезности описывается функцией полезности кобба дугласа.

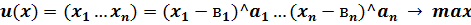
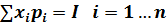
Смысл модели Стоуна:

1. Сначала приобретается необходимое количество каждого вида товвара (в)

2. После приобретения расчитывается оставшаяся сумма.

3. Оставшаяся сумма распределяется между всеми видами товаров в соответствии с весовыми коэффициентами аi.

4. Т.о. определяется количество доп ед каждого вида товара, которые необходимо для приобретения потребителю.

12. Двойственная задача потребительского выбора.

Предположим что потребитель не стремится приобрести набор товаров, обеспечивающих ему максимальную полезность, предположим, что потребитель выбрал уровень полезности U*, который его устраивает. Среди всех наборов товаров потребитель стремится выбрать самый дешевый.

Математическая постановка:

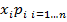∑ -> min

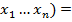U( U*

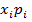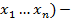L(x1…xn,λ) = ∑ -λ(U( U*

Условие первого порядка: отношение предельной полезности = отношению цен):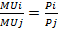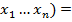

U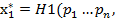( U*

U*)

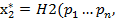U*) <-функция спроса Хикса

…

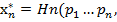U*)

13. Эластичность функции. Определение и свойства.

Эластичность функции f(x) называется предел отношения относительного приращения функции к относительному приращению аргумента, когда приращение аргумента стремится к 0.

=…=

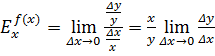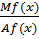
Свойства эластичности функции:

1. Эластичность представляет из себя безразмерную величину.

2. Эластичность 2х взаимообратных функций представляет собой взаимообратные величины:

3. Эластичность произведения 2х функций равна сумме эластичностей этих функций:

4. Эластичность суммы 2х функций:

5. Эластичность частного 2х функций

14. Свойства функций спроса Маршалла. Перекрестная эластичность. Взаимозаменяемые и взаимодополняемые товары.

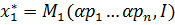
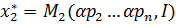
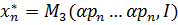
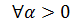
1.Функции спроса маршалла являются однородными функциями нулевой степени.

2.Свойство показывает как реагирует спрос в ответ на изменение цены и дохода потребителя (| 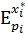| >1….<1….=1….=0…

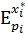| | <1 – спрос не эластичен, 1% е увеличение цены изменяет спрос на товар меньше чем на 1%

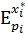| | =1 – 1%е изменение цены изменяет спрос на товар на 1%

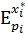| | >1 – эластичный спрос- 1%е увеличение цены ведет к увеличению спроса больше чем на 1%

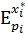| | =1 – совершенно эластичный спрос- 1%е увеличение цены ведет к бесконечному увеличению спроса на товар.

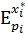| | =1 – 1%Е ИЗМЕНЕНИЕ ЦЕНЫ НЕ ВЛИЯЕТ НА СПРОС.

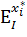| | - для эластичности дохода тоже справедливы выше указанные случаи.

Перекрестная эластичность- относительное изменение спроса на i-тый товар в ответ на 1% изменение цены j-го товара. Обозначается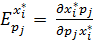

Случай 1. Перекрестная эластичность положительная.

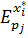> 0 тов iи j – являются взаимозаменяемыми, т.е. 1% увеличение цены на 1 товар вызывает увеличение спроса на другой товар.

Случай 2. Перекрестная эластичность отрицательная.

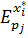< 0 товары являются взаимодополняемыми, т.е. 1% увеличение цены на 1 товар вызывают снижение спроса на др.

15. Кривые «доход – потребление» и «цена – потребление», построение.

Кривая доход – потребление показывает как изменяется рациональный выбор потребителя в зависимости от изменения дохода.

Кривая цена – потребление показывает как влияет изменение цены на выбор товара.

16. Уравнение Слуцкого. Геометрическая иллюстрация.Эффект дохода и эффект замены....

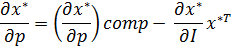
Уравнение используется для расчета компенсации, для классификации товаров.

Геометрическая интерпретация:

1. Назовем товары i и j взаимозаменяемыми, если соответствующий эффект замены положителен. 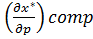> 0

2. Назовем товары i и j взаимодополниемыми, если соответствующий эффект замены отрицателен. 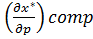<0

3.Назовем товары i и j ценными, если при увеличении дохода спрос на этот товар увеличивается. 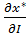> 0

4.Товар называется малоценным, если при увеличении дохода спрос на этот товар уменьшается. 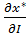< 0

5.Товар называется нормальным, если при увеличении цены спрос на товар падает. 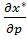< 0

6.Товар называется товаром Гиффена, если при увеличении цены спрос на него растет. 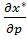>0

17. Пространство затрат. Производственная функция. Предельный продукт. Свойства производственной функции. Основные виды производственных функций.

Пространство выпуска – S - множество векторов выпуска продукции.

S =

Пространство затрат – R – множество затрат факторов производства.

R =

Технологическая связь между затратами и объемом выпуска описывается с помощью технологической функции. q = f(x)(явный вид) – функция которая каждому вектору затрат ставит в соответствие максимальный выпуск который может быть произведен при данных затратах.

(неявный вид) – F(x,q,A) = 0, А- технологическая матрица размером m x n

Функция выпуска – если в качестве независимых аргументов рассматриваются затраты.

Функция затрат – если в качестве независимых аргументов рассматривается выпуск.

Предельным продуктом i – го фактора производства называют доп объем выпуска который будет произведен при потреблении каждой доп ед каждого вида товара.

Свойства производственной функции:

1.С увеличением потребления какого либо фактора производства значение выпуска продукции возрастает.

2.С увеличением объема потребления какого либо фактора производства скорость выпуска продукции убывают.

3.Производственная функция является однородной функцией своего аргумента. F(t,x)= 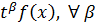, 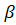– степень однородности.

Основные виды производственной функции:

1. Производственная функция вида Кобба – Дугласа:

2. Производственная функция Леонтьева:

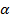– пропорции в которых осуществляется потребление затрат факторов производства для осуществления выпуска одной ед продукции.

3. Линейная производственная функция

4. Квадратичная функция.

5. Квазилинейная функция

18. Модель совершенной конкуренции. Краткосрочный и долгосрочный периоды производства.

Модель предполагает наличие на рынке большого числа фирм производящих данную продукцию и потребляющих одинаковые факторы производства. Это означает что ни один из участников рынка за счет выбранной им стратегии производства не может повлиять на цену ед выпуска и на цену факторов производства. Все участники являются ценополучателями.

Задача производителя может рассматриваться в условиях краткосрочного и долгосрочного периода.

Краткосрочный период – предполагает что период производства является не достаточно длительным для того что бы фирма могла полностью задействовать все ресурсы производства продукции, т.е. фирма ограничена в потреблении того или иного факторов производства.

В долгосрочном периоде – период производства достаточно длительный и фирма может задействовать все ресурсы, отсутствуют издержки связанные с началом производства продукции.

19. Задача производителя в долгосрочном периоде. Мат. Постановка. Отыскание функций издержек. Условие первого порядка. Максимизация прибыли.

Предполагается что цель фирмы заключается в максимизации прибыли путем выбора видов и количества затрат, при заданной технологии производства, производственной функции путем выбора P и W.

Мат. постановка:

П(q)= R- C -> max

F(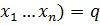 - производственная функция.

R=p*q C = 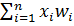В итоге нужно найти q=?

Решение: 1й этап. Нахождение функции издержек, Т.е. нужно определить зависимость издержек производства от объема выпуска продукции. (с какими мин издержками производитель может осуществить выпуск продукции заданного объема)

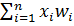- > min усл. первого порядка:

F( =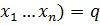

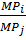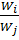
F(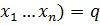

В итоге получится: =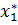

=

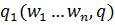
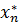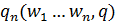
2й этап: Нахождение максимизации прибыли.

П(q) = p*q – C(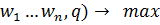

q = F(p,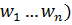

p = 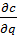- решение производителя в усл сов конкуренции.

Т.о. прибыль будет максимальной, когда предельные издержки равны ед продукции.

Предельные издержки (MC) — это издержки, связанные с производством дополнительной единицы продукции.

20. Задача производителя в краткосрочном периоде. Мат постановка. Этапы решения.

Предполагается что цель фирмы заключается в максимизации прибыли путем выбора видов и количества затрат, при заданной технологии производства, производственной функции путем выбора P и W. в краткосрочном периоде у производителя могут возникнуть ограничения в объеме потребления того или иного фактора производства.

П(q)= R- C -> max

F(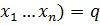

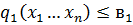- ограничения на объемы

… потребления факторов производства.

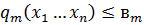
В такой постановке если не накладывать ограничения q то универсальных методов решения не существует.

Точно также, как и в долгосрочном периоде решение задачи фирмы разбивается на два этапа:

1. нахождение функции издержек (решение задачи минимизации издержек),

2. нахождение объема выпуска, максимизирующего прибыль производителя.

Следует отметить, что в условиях краткосрочного периода производитель несет большие издержки, чем в долгосрочном периоде (при одинаковых ценах выпуска и факторов производства).

21. Изокванты и изокосты. Уравнения и графики изоквант для основных видов производственных функций. Уравнение изокосты и график.

Изокванты – уровня q* производственной функции q = f(x) называется множество всех векторов затрат факторов производства, использование которых приводит к выпуску q* ед продукции.

1. Линейная функция.

Производственная функция - f(x1x2) = a1x1+a2x2

Уравнение изокванты – a1x1+a2x2 = q*

График:

2. Функция Кобба – Дугласа.

Производственная функция -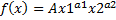

Изокванта -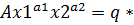

График:

3. Функция Леонтьева

Производственная функция - ;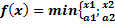

Изокванта -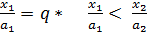

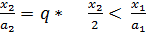
График:

Изокостой уровня с* называется множество всех вектров затрат факторов производства стоимость которых равна с*

Изокосты ны зависят от вида производственной функции.

Уровнение изокосты: *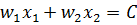

График:

22. Графическая интерпретация решения задачи фирмы.

Предположим, что в производстве продукции задействовано два фактора:

х1- количество единиц первого товара, х2- количество единиц второго товара.

Тогда производственная функция имеет следующий вид: q = f(x1, x2). 1.Рассмотрим уравнение изокванты уровня q*: f(x1, x2)= q*

2. Рассмотрим х2 как функцию от х1: f(x1,x2(x1) = q*

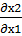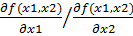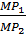
3.Найдем производную от х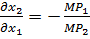1

=- = - (1)

Рассмотрим уравнение изокосты C*: *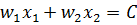

Рассмотрим x2 как неявную функцию от переменной x1.

w1x1 + w2x2(x1) = C*

Продифференцируем по переменной x1 обе части равенства. Получаем:

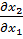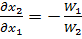w1 + w2 = 0 (2)

Величина (1) – называется технологической нормой замещения факторов производств, она показывает в какой пропорции один фактор производства может быть заменен другим без изменения объема выпуска.

Условие первого порядка для минимизации издержек производства (выполняется в точке равновесия)

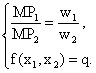
Используя соотношения (1) и (2) получим, что: - 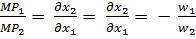(выполняется в точке минимальных издержек.) (изокванта) (изокоста)

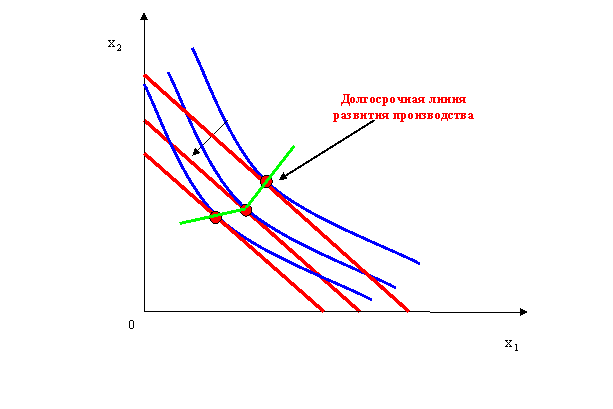
Это означает, что в точке, соответствующей минимальной стоимости затрат для производства заданного объема выпуска, наклон касательной к изокванте соответствующего уровня совпадает с наклоном изокосты, т. е. этой точкой является точка касания изокванты и изокосты.

Данную линию называют долгосрочной линией развития производства. Эта линия показывает, каким образом должно изменяться соотношение потребления факторов производства для увеличения выпуска продукции с минимальными издержками.

23. Модель несовершенной конкуренции. Монополия и монопсония.

На рынке присутствует ограниченное число фирм производителей данной продукции, в следствие чего каждый из участников рынка способны вызвать изменение P и W (цен производственных ресурсов и цен на выпуск продукции). Т.о. каждый производитель вынужден учитывать возможную реакцию конкурентов.

Монополия.

Пусть на рынке присутствует только одна фирма выпускающая продукцию.

q- объем выпуска продукции.

P= p(q)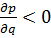

Уменьшая объем предложения продукции монополист может заставить потребителя покупать товар по более высокой цене 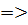функция p(q) – убывающая функция.

Выручка монополиста: R(q) = q*p(q)

Предельная выручка: MR(q) =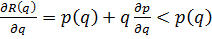

Т.о. в условиях монополии, выручка производителя за доп ед продукции меньше чем цена ед продукции.

Монопсония.

Пусть на рынке присутствует только один потребитель соответствующих ресурсов.

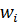– цена iго фактора производства.

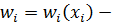зависит от объемов фактора производства.

Очевидно что монополист может приобрести болешее количество того или иного продукта только предложив большую смму за ед продукции => функция 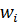– возрастающая.

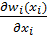> 0

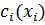–издержки связанные с потреблением i – го фактора производства.

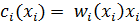
Найдем предельные издержки связанные с потреблением каждой доп ед соответствующего фактора производства:

=

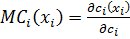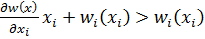
В условиях монопсонии за каждую доп ед того или иного ресурса фирма платит цену большую чем цена этого ресурса.

24. Решение задачи монополиста. Неэффективноть монополии.

Фирма стремится получить максимальную прибыль, с учетом имеющейся у нее технологии производства.

P(q)q –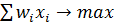

q = f(x1…xn)

L(q,xi,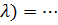

=… = …

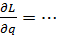
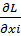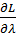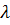=MR(q) – пред доход. MC – пред издержки.

MR(q) 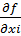= MCi(xi)

q = f(x1…xn)

Разделим обе части ур на :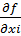

MR(q) = MCi(xi)/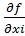

Рассмотрим производственную функцию как функцию затрат:

MR(q*) = MC(q*) – уравненение определяющее оптимальный выпуск q* фирмы в усл монополии.

В условиях монополии общественное благо всегда недопоставляется это называется неэффективностью монополии.

25. Дуополия. Условие равноавесия по Нэшу.

Олигополия – ситуация когда на рынке присутствует насколько производителей данного рынка. Олигопсония – ситуация когда на рынке присутствует несколько потребителей данного рынка.

Дуополия – 2 фирмы. Дуопсония – 2 потребителя.

Дуополия.

У каждой фирмы существует своя собственная технология производства.

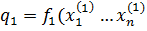
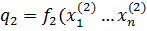
qi- выпуск продукции i – й фирмой. 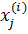– величина потребления затрат j – того вида i – той фирмой. P определяется предложением отросли.

P(q1,q2) – зависит от первого и второго выпуска.

Увеличение предложения продукта приводит к снижению цены.

При увеличении потребления какого либо вида производства происходит рост цены на этот фактор производства.

Прибыль зависит не только от выбранной стратегии пр – ва но и от стратегии конкурента.

Будем предполагать что целью каждой фирмы является максимизация собственной прибыли.

П1 = P(q1,q2) q1 - 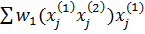-> max

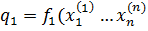
Задачи принятия решений

П2 = P(q1,q2) q2 - 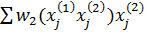-> max в конфликтной ситуации

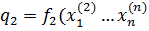
Условие равновесия по Нэшу:

(P + 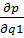q1) 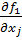= 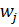j = 1…m

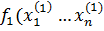= q1 первая фирма

(P + 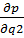q2) 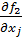= 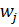j = 1…m

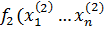= q2 вторая фирма

26.Дуополия Курно.

Модель дуополии где ценообразование на рынке пассивное, т.е. цена определяется равновесием спроса и предложения. Оба участника уверены, что при изменении ими объема производства их конкурент не отреагирует и сохранит свой объем производства на прежнем уровне.

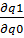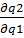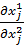= 0 = 0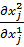

= 0 = 0

27. Динамика равновесия Курно.

28. Модель дуополии Штакельберга. Равновесие Штакельберга.

Модель дуополии в которой один игрок либо оба считают что его еонкурент взаимодействует с ним согласно модели Курно(Модель дуополии где ценообразование на рынке пассивное, т.е. цена определяется равновесием спроса и предложения, оба участника уверены, что при изменении ими объема производства их конкурент не отреагирует и сохранит свой объем производства на прежнем уровне) – называется моделью дуополии Штакельберга.

Первый дуополист предполагает реакцию своего конкурента согласно модели Курно и является для модели Штакельберга лидером. Второй дуополист в этом случае называется последователем.

П1 = (а – б(q1+q2))q1 – c – 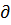q1

П2 = (а – б(q1+q2))q2 – c – 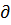q2

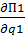= (а – б(q1+q2))- q1(a – бq1 – бq2) - 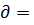(а – б(q1+q2)) – q1(-б – 1/2б)- =

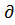=а-б(q1+q2) + бq1(1 – ½) –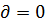

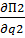= (а – б(q1+q2))+бq2(1 – ½) –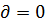

=

= -

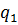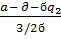
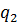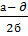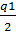
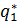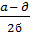= оптимальные

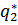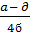= стратегии

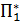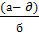= 1/8

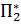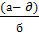= 1/16

=

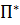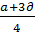
Равновесие Штакельберга:

, , ,)

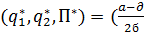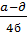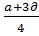В итоге – лидер обеспечиваетсебе прибыль в 2 раза больше чем последователь.

30. Неравновесие Штакельберга.

Предположим что 2й игрок не захотел стать последователем, а захотел стать тоже лидером, тогда будем иметь что обе вариации = - ½

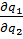= -1/2 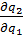= -1/2

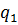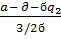= <- их оптимальные стратегии

=

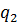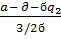
Найдем оптимальные выпуски.

= =

=

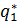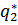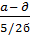
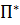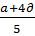
Неравновесие Штакельберга:

, , ,)

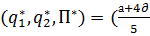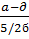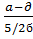В итоге – ситуация когда оба дуополиста догадываются о использовании конкурентом модели Курно, прибыль получают они в 2 раза меньше.

31. Картель.

Если один из игроков решает стать лидером а 2й игрок продолжает быть последователем, то лидер получит в 2 раза больше чем последователь=> для обоих игроков будет безопаснее оказаться в ситуации неравновесия штакельберга.

В теории игр подобная проблема называется делемой заключенного.Отсутствие информации мешает обоим дуополистам получить максимальную прибыль, т.е. таким образом создать картель.

Предположим, что производители договорились о равном разделе полученной картели прибыль, тогда предложение продукции отраслью

q= q1+q2; p=a+bq, c – будут равны сумме издержек каждого из производителей. С=(с-dq1+c – dq2) = 2c+dq

П=(а-bq)q-2c-dq

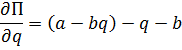
P*=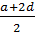

*=

*=

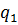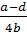
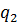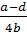
П = 1/8 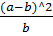-c

32. Основные задачи теории рыночного равновесия.

Модель рынка.

На рынке происходит взаимодействие между потребителями и производителями.

Поведение всей совокупности потребителей присутствующей на рынке приводит к формированию рыночного спроса на тот или иной товар.

А деятельность присутствующих на рынке фирм(производителей) приводит к формированию рыночного предложения продукции.

Потребители располагают набором факторов производства(труд, ресурс)который они продают на рынке товаров. Производители покупают факторы производства с тем что бы продавать произведенную продукцию на рынке товаров.

Т.о. в теории рыночного равновесия задаются предпочтения и ресурсы потребителя.

Для фирмы производственная функция:

Цены товаров и факторов производства были заданы. Определяет взаимодействие условий спроса и предложения и определяет каким образом это взаимодействие влияет на цены на обоих рынках (цены товаров и факторов производства)

Рассмотрим некий товар, если спрос на товар увеличивается, то цены будут повышаться и наоборот. Этот процесс будет продолжаться до тех пор, пока цена товара не будет равна предложению.

Объем товара = объем предложения – рыночное равновесие.

Рыночное равновесие – общее количество каждого товара, которое индивид хочет купить по текущим ценам совпадает с предложением этого товара на рынке.

Основные задачи:

1. Определение существования рыночного равновесия. (Возможен ли при заданных параметрах рынка переход рынка в равновесное состояние?)

2. Единственность рыночного равновесия(является ли точка рыночного равновесия единственной или существуют альтернативные стабилизации рынка?)

3. Устойчивость рыночного равновесия(Долго ли может просуществовать рынок в точке рыночного равновесия?)

33. Паутинообразная модель.

Переход рынка в состояние равновесия.

Предполагается что рынок описывается с помощью кривых спроса (D(p)) и кривых предложения (S(p)). Будем предполагать что функции спроса и предложения являются линейными.

S(p) = a+bp,a>0

D(p) = d-cp, d<0

найдем точку рыночного равновесия.

S(p) = D(p)

a+bp = d-cp

bp+cp = d-a

p(b+c) = d-a

p*= 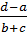- точка рыночного равновесия.

Паутинообразная модель перехода рынка в состояние равновесие получается сл образом. Разобьем ось времени на равные промежутки и пронумеруем от 0 до n.

На интервале t продается товар произведенный на интервале t-1. На этом интервале было произведено товаров S(pt-1) На интервале t его продавали по цене Pt, тогда спрос на товар D(pt), считая, что спрос = предложению, получаем: D(pt)=S(pt-1)

Подтавив и решив выражение, нашли Pt, отсюда выведем q, и получим q= -

1ситуация. Стабилизация рынка. Происходит в том случае, когда <1

Наклон кривой спроса к положительному направлению оси абсцисс будет круче чем наклон кривой предложения.

В этом случае точка t

будет точкой пересечения ->

т.е. рыночным равновесием.

2 ситуация. рынок испытывает цикл роста и спада производства =1

Наклоны кривых совпадают. Рыночная цена совершает колебания равные амплитуде вокруг точки рыночного равновесия. Эти колебания являются прообразами экономических циклов роста и спада производства.

3 ситуация. Дестабилизация рынка. 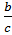>1

Наклон кривой спроса меньше наклона кривой предложения. Колебания с постоянно увеличивающейся амплитудой => крах рынка.

34. Модель общего рыночного равновесия Вальраса. Вывод условия первого порядка.

Пусть имеется экономика в которой выпускается n – видов продукции с помощью m – факторов производства.Будем считать что рынок функционирует в условиях совершенной конкуренции. Будем считать что на рынке присутствует к-фирм, каждая из которых может производить любой вид продукции. Обозначим через qi – вектор вупуска i-той фирмы. Обозначим через xi – вектор затрат. 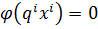– заданная функция выражена в неявном виде.

Задача производителя:

Цель производителя максимизация прибыли, тогда для i-той фирмы:

П=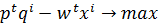

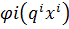=0 i- 1…к

Вывод условия первого порядка для задачи производителя:

)

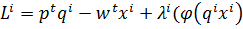i-номер фирмы λ – множитель лагранжа для каждой фирмы.

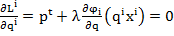
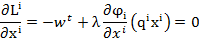
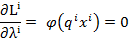
Задача потребителя:

Кроме того в экономике имеется L- потребителей, каждый из которых владеет определенным фактором производств. (Может продать свою раб.силу и получить доход) 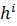- набор товаров приобретаемых i-ым потребителем. 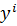- набор факторов производстванаходящихся в распоряжении i-го потребителя. I=1…L

Потребитель получает определенную долю прибыли каждой фирмы(зарплата). 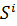-вектор долей участия i-го потребителя в прибыли фирм.

Функция полезности -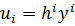

Мат постановка задачи потребителя:

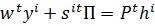
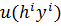-> max

= (

=

=

=

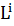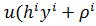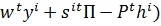
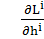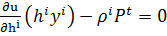
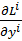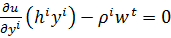
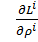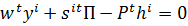
35. Законы Вальраса.

Рассмотрим условие первого порядка для производителя и потребителя соответственно. Из определения рыночного равновесия следует, что общая сумма спроса на любой товар фактор производства должна быть равна сумме предложения этого товара или фактора производства.

Равновесие на рынке товаров:

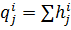∑ j=1…n, i= 1….k

Равновесие на рынке ресурсов:

∑

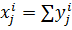
Рассмотрим бюджетное ограничение для потребителей:

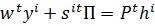
Просуммируем его по всем L-потребителям:

П-представляет из себя суммарную прибыль всех фирм

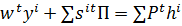∑ , где i-1…L - 1й закон Вальраса.

1й закон Вальраса: В усл рвночного равновесия общий доход потребителей вместе с общей прибылью всех фирмдолжен равняться общей стоимости товаров.

Воспользуемся определением прибыли фирм, тогда первый закон можно записать сл образом:

∑

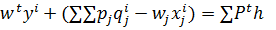
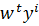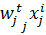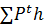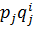∑ -∑∑ = - ∑∑ – 2й закон Вальраса

Избыточный избыточный

спрос на ресурсы спрос на товары

2й закон Вальраса:

Стоимость совокупного избыточного спроса тождественно равна нулю.

36.Стратегическая модель Леонтьева.

(модель межотраслевого баланса)

1.Пусть экономика состоит из n – отраслей. Предположим что в экономике производится, продается, покупается, потребляется, инвестируется n-видов продукции.

2. Каждая отрасль является чистой, т.е. производит только 1 вид продукции. Различные отрасли выпускают различную продукцию.

3. Под производственным процессом в каждой отрасли понимается преобразование некоторых типов продуктов в определенный конечный продукт.

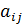- количество ед i-го продукта, необходимого для производства j-го продукта.

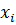- валовый выпуск i-го продукта за год.

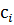- потребление выпуска отрасли в непроизводственной сфере(СПРОС)

Количество продукта которое используется по всем отраслям:

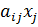∑ j- 1…n

Чистый продукт:

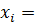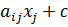∑ <-Статистическая модель Леонтьева.

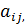
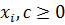Координатная запись модели.

Модель Леонтьева позволяет определить валовый продукт отрослей по заданному спросу- 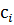. Все величины модели должны бить неотрицательными.

Величины 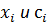могут быть использованы в натуральных или стоимостных измерениях, т.о. межотраслевой баланс может быть либо натуральным либо стоимостным.

X=(x1,…xn)^T вектора

C=(c1….cn)^T

А= 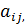i,j – матрица коэф-ов

Х=АХ+С <-Статистическая модель Леонтьева. -> (Е-А)х=с

Х,A,c> 0 матричная запись модели.

Уравнение Леонтьева может быть получено из модели Вальраса, если в качестве производственной функции взять производственную функцию Леонтьева.

36. Продуктивность модели Леонтьева.

Система Х=АХ+С называется продуктивной, если она разрешена в неотрицательных значениях переменной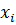

Что бы найти решение системы, запись (Е-А)х=с умножаем на матрицу обратную к матрице (E-A)

Т.о. х=(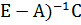 -> если обратная матрица существует и она положительна, то решение будет положительным 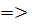модель Леонтьева будет продуктивной.

Условия:

1.Матрица 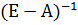- должна быть неотрицательно определена.

Проверить можно использовав критерий Сильвера – матрица будет неотрицательно определена, если все ее миноры имеют чередующиеся знаки начиная с отрицательного.(критерий применяется когда n<10)

2.Бесконечный матричный ряд вида Е+А+А^2…- сходится и его сумма =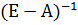

3.Модель Леонтьева будет продуктивной если наибольшее собственное значение матрицы А по модулю меньше единицы.|Е-λА|=0 λ-собств.число.

|λmax|<1

Если модель Леонтьева продуктивна, то для любого вектора конечного спроса с 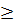0 однозначно определяется неотрицательные вектор валового продукта-т.е. х.

X=C+A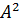C+ C+…

Матрица 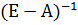>0 – называется матрицей полных затрат, обозначается А*. Используя А* можем записать решение модели Леонтьева в матричном виде:

Х=А*С.

38.Рыночное равновесие модели Леонтьева.

Может быть использована для нахождения рыночного равновесия. При ее использовании находятся объемы спроса и потребления, гарантировано положительные величины.

Обозначения:

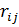- количество iго фактора производства, необходимое для обеспечения выпуска jтой отрасли xj. Определяется: 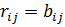xj

Где 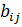– матрица технологических коэффициентов факторов производства.

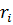- объем предложения iго фактора производства.

Просуммируем соотношение по выпускам всех отраслей и получим спрос всей экономики на эти факторы производства:

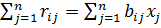i=1…m

=

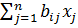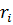
Bx<r - в матричном виде.

Прямая задача:

Заключается в максимизации национального продукта.

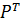C->max

p-цены, С- заданный объем.

(обычная задача линейного программирования)

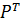C->max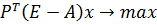

X=Ax+C упростим -> Bx<r

Bx<r x>0

x 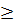0

Двойственная задача:

Минимизация стоимости национального продукта.

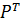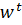A + B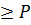

w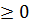

Что бы найти рыночное равновесие нужно решить 2 задачи прямую и двойственную.

39. Динамическая модель Леонтьева.

Рассмотрим модель Леонтьева во времени и предположим что из выпуска каждой отрасли выделяются инвестиции для развития каждой отрасли.

Будем рассматривать инвестиции как функции прироста производства от момента времени (t-1) до момента (t)

X(t) = 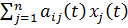+ 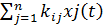- 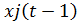+ 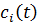i=1…m

Где

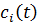- объем конечного потребления продукта в момент времени t

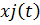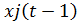- – прирост валовой продукции iтой отрасли

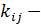доля инвеслиций iтой отрасли в приросте продукции jтой отрасли.

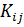-объем инвестиция i-той отрасли в j-ю

=

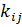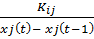
В матричном виде:

X(t)=A(t)X(t)+k(t)(x(t)-x(t-1))+c(t)

Решение:

X(t) – A(t)x(t)-k(t)x(t)=c(t)-k(t)x(t-1)

(E-A(t) – k(t))x(t)=c(t)-k(t)x(t-1)

X(t)=(E-A(t)-k(t))^-1 c(t)-k(t)x(t-1)

X(t) – спрос в момент времени t зависит от предыдущего x(t-1)

---

Дата добавления: 2015-10-23