Приклад 11. Метод Четверикова

Застосувати метод Четверикова для виділення компонент часового ряду, приведеного в табл. 12.6.

Розв’язання

1. Проведемо вирівнювання емпіричного ряду 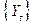з використанням центрованої плинної середньої з періодом згладжування .

Отриману попередню оцінку тренду 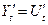віднімаємо з початкового емпіричного ряду

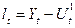чи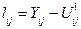

2. Обчислюємо для кожного року 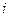і (по рядку) середньоквадратичне відхилення 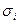величини , використовуючи для цього формулу:

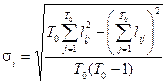
Таблиця 12.7. Значення величин :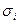

t
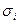
	1,22	1,29	1,60	1,54	2,00	1,63	1,38	1,83	1,82	1,69	1,67	1,90	5,55

При обчисленні до уваги беруться тільки шість останніх рівнів першого року: 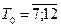, а при обчисленні 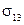– перші шість рівнів тринадцятого року: .

Ділимо окремі значення кожного місяця з табл. 12.6 на відхилення відповідного року. В результаті отримуємо табл. 12.7, в якій

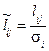
3. Останній рядок табл. 12.7 є значеннями попередньої середньої сезонної хвилі, обчисленої за формулою:

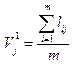
Таблиця 12.7. Нормований залишковий ряд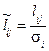

Рік	Місяць
							1,19	1,31	0,84	0,43	-0,79	-0,65
	-1,48	-1,85	-0,49	0,03	0,36	0,85	1,09	1,31	0,54	0,73	-0,31	-0,67
	-1,38	-1,69	-0,19	-0,04	0,78	0,81	1,25	1,23	0,36	0,50	-0,78	-0,94
	-2,04	-1,18	-0,25	0,27	0,75	0,93	1,07	1,08	0,70	0,64	0,01	-0,84
	-1,48	-2,07	-0,67	-0,11	0,85	1,03	0,98	0,91	0,39	0,24	-0,32	-0,54
	-1,42	-1,85	-0,42	0,07	0,98	1,13	1,05	0,85	0,51	0,24	-0,43	-0,90
	-1,43	-1,74	-0,81	0,25	1,07	1,04	0,74	1,21	0,92	0,44	-0,25	-0,24
	-1,96	-2,62	-0,70	0,05	0,73	0,98	0,83	0,95	0,85	0,27	-0,33	-0,31
	-1,76	-1,65	-0,37	0,06	0,69	0,95	1Д4	1,08	0,40	0,36	-0,32	-0,90
	-1,53	-1,99	-0,31	0,30	0,89	0,75	1,09	0,97	0,49	0,42	-0,22	-0,79
	-1,30	-1,86	-0,68	-0,11	0,75	0,88	0,96	1,18	0,83	0,41	-0,77	-0,50
	-1,41	-2,02	-0,01	0,03	1,16	0,75	0,84	1,09	0,89	0,17	-0,26	-0,55
	-0,66	-0,67	-0,10	-0,01	0,29	0,25
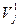
	-1,49	-1,68	-0,42	0,07	0,78	0,86	1,02	1,10	0,64	0,40	-0,40	-0,65

Таблиця 12.8.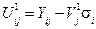

Рік	Місяць
							10,21	10,34	10,42	10,28	9,83	10,34
	10,42	10,28	10,47	10,61	10,23	10,87	11,06	11,31	11,01	11,67	11,49	11,47
	11,78	11,69	12,11	11,62	11,80	11,71	12,11	11,98	11,39	12,05	11,22	11,49
	11,13	12,77	12,29	12,38	12,08	12,31	12,31	12,13	12,12	12,34	12,63	11,75
	12,13	11,38	11,71	11,87	12,40	12,67	12,37	12,25	12,28	12,59	13,20	13,35
	13,31	12,98	13,31	13,39	13,76	13,93	13,58	13,23	13,47	13,47	13,74	13,41
	13,92	13,79	13,39	14,24	14,46	14,42	13,81	14,31	14,58	14,28	14,48	14,90
	13,57	14,62	14,08	14,65	14,65	15,03	14,54	14,71	15,48	14,95	15,40	15,94
	14,90	15,54	15,60	15,52	15,43	15,75	15,83	15,62	15,23	15,64	15,92	15,35
	15,73	15,30	16,04	16,28	16,12	15,81	16,17	15,90	15,89	16,17	16,46	15,96
	16,57	16,00	15,96	16,18	16,48	16,63	16,61	16,87	17,18	17,03	16,54	17,56
	17,56	16,85	18,39	17,61	18,49	17,65	17,50	17,86	18,36	17,47	18,17	18,11
	22,56	23,64	19,83	17,71	15,49	13,94

4. Попередню середню сезонну хвилю 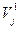множимо на середньоквадратичне відхилення кожного року 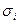і віднімаємо з початкового емпіричного ряду: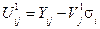

В результаті отримуємо ряд, позбавлений попередньої сезонної хвилі (табл. 12.8).

5. Часовий ряд, позбавлений попередньої сезонної хвилі, згладжуємо з використанням простої плинної середньої з інтервалом згладжування, рівним п’яти, і отримуємо нову оцінку тренду (табл. 12.9).

Таблиця 12.9. Нова оцінка тренду

Рік	Місяць
									10,22	10,24	10,26	10,23
	10,27	10,42	10,40	10,49	10,65	10,82	10,90	11,18	11,31	11,39	11,48	11,62
	11,71	11,73	11,80	11,79	11,87	11,84	11,80	11,85	11,75	11,63	11,46	11,73
	11,78	12,02	12,13	12,37	12,27	12,24	12,19	12,24	12,31	12,19	12,19	12,05
	11,92	11,79	11,90	12,01	12,20	12,31	12,39	12,43	12,54	12,73	12,95	13,09
	13,23	13,27	13,35	13,43	13,59	13,58	13,59	13,54	13,50	13,46	13,60	13,67
	13,65	13,75	13,96	14,06	14,06	14,25	14,32	14,28	14,29	14,51	14,36	14,37
	14,33	14,36	14,31	14,61	14,59	14,72	14,88	14,94	15,02	15,30	15,33	15,35
	15,48	15,50	15,40	15,57	15,63	15,63	15,57	15,61	15,65	15,55	15,57	15,59
	15,67	15,74	15,89	15,91	16,08	16,06	15,98	15,99	16,12	16,08	16,21	16,23
	16,19	16,13	16,24	16,25	16,37	16,55	16,75	16,86	16,85	17,04	17,17	17,11
	17,38	17,59	17,78	17,80	17,93	17,82	17,97	17,77	17,87	17,99	18,93	19,99
	20,46	20,37	19,85	18,12

6. Обчислюємо відхилення ряду від початкового емпіричного ряду :

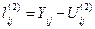
Отримані відхилення піддаємо обробці відповідно до пп. 2 і 3 для виявлення нових значень сезонної хвилі. Отримуємо наступні значення:

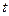
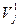
	-1,54	-1,81	-0,43	0,08	0,82	0,93	1,01	1,09	0,63	0,41	-0,40	-0,72

При порівнянні значень коефіцієнтів сезонної хвилі, отриманих на першій і другій ітераціях, т. е. значень 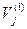і , неважко помітити, що вони трохи відрізняються один від одного.

7. Обчислюємо коефіцієнт напруженості сезонної хвилі в такому порядку: за формулою фактично отримуємо значення випадкової компоненти, які для нашого прикладу приведені в табл. 12.10.

Таблиця 12.10. Обчислення значень випадкової компоненти

Рік	Місяць
	-0,23	-0,50	-0,04	0,13	-0,23	0,23	0,47	0,46	-0,10	0,39	-0,11	-0,27
	-0,77	-0,92	0,07	-0,14	0,36	0,32	0,93	0,80	0,03	0,65	-0,48	-0,56
	-1,4	-0,02	-0,06	0,04	0,13	0,46	0,68	0,49	0,17	0,36	-0,22	-0,58
	-1,23	-1,96	-0,60	-0,08	0,94	1,15	1,01	.0,93	0,39	0,25	0,15	-0,32
	-0,81	-1,22	-0,29	-0,05	0,62	0,82	0,64	0,39	0,38	0,25	-0,11	-0,60
	-0,25	-0,47	-0,72	0,20	0,66	0,43	-0,11	0,46	0,54	-0,09	-0,03	0,35
	-1,95	-1,00	-0,57	0,09	0,67	0,95	0,5 2	0,69	1,00	-0,03	0,26	0,12
	-1,75	-1,21	-0,13		0,40	0,76	1,11	0,92	0,11	0,41	0,02	-0,70
	-0,92	-1,47	-0,13	0,41	0,54	0,27	0,90	0,68	0,22	0,36	-0,03	-0,65
	-0,57	-1,13	0,56	-0,03	0,59	0,59	0,55	0,76	0,77	0,25	-0,90	0,08
	-1,13	-2,12	0,24	-0,14	1,22	0,53	0,46	1,09	1,08	-0,17	-1,12	-2,40
	-0,23	-0,50	-0,04	0,13	-0,23	0,23	0,47	0,46	-0,10	0,39	-0,11	-0,27

З використанням співвідношення:

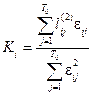
визначаємо величини коефіцієнта напруженості для кожного року, окрім першого і останнього.

Таблиця 12.11. Значення коефіцієнта напруженості сезонної хвилі

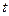
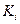
	3,02	2,47	2,44	2,09	2,48	2,48	2,41	2,10	2,34	2,08	1,79

8. Використовуючи коефіцієнт напруженості обчислюємо остаточні значення сезонної компоненти часового ряду (табл. 12.12): .

Таблиця 12.12. Сезонна компонента часового ряду

-4,65	-5,47	-1,30	0,24	2,48	2,81	3,05	3,29	1,90	1,24	-1,21	-2,17
-3,80	-4,47	-1,01	0,20	2,03	2,30	2,49	2,69	1,56	1,01	-0,99	-1,78
-3,76	-4,42	-1,04	0,20	2,00	2,27	2,46	2,66	1,52	1,00	-0,96	-1,76
-3,22	-3,78	-0,90	0,17	1,71	1,94	2,11	2,28	1,25	0,86	-0,84	-1,50
-3,82	-4,49	-1,07	0,20	2,03	2,31	2,50	2,70	1,56	1,02	-0,99	-1,78
-3,82	-4,49	-1,07	0,20	2,03	2,31	2,51	2,70	1,56	1,02	-0,99	-1,79
3,71	-4,36	-1,04	0,19	1,98	2,24	2,43	2,63	1,52	0,99	-0,96	-1,74
-3,23	-3,80	-0,90	0,17	1,72	1,95	2,12	2,29	1,32	0,86	-0,84	-1,51
-3,60	-4,24	-1,01	0,19	1,92	2,18	2,36	2,55	1,47	0,96	-0,94	-1,68
-3,20	-3,76	-0,89	0,17	1,71	1,93	2,10	2,27	1,31	0,85	-0,83	-1,50
-2,76	-3,24	-0,77	0,14	1,47	1,66	1,81	1,95	1,13	0,73	-0,72	-1,29

Дата добавления: 2015-10-23