Алгоритм деления в системе с отрицательным основанием.

28. ПОМЕХОЗАЩИТНЫЕ КОДЫ. КОД ХЭММИНГА
Код Хэмминга позволяет автоматически исправлять ошибки, возникающие в отдельных кодовых словах.
Это, в частности, необходимо при хранении данных в полупроводниковой памяти. Возникающие здесь ошибки появляются в различных разрядах независимо, а это значит, что вероятность однократной ошибки на несколько порядков выше, чем двукратной, трехкратной и т.д.
Общая схема кодирования – декодирования по Хэммингу показана на рис.9.1.

При кодировании передаваемые информационные разряды х1..хк дополняются m избыточными разрядами таким образом, чтобы полученный кодовый вектор Х {х1…хn} отвечал условию ортогональности некоторой проверочной матрице, состоящей из m строк.
В развернутом виде запись условия ортогональности выглядит как система из m уравнений вида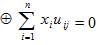

(здесь j = 1,m – номер проверочного уравнения).
Собственно процедура кодирования как раз и состоит в нахождении проверочных разрядов хк+1…хк+m по m уравнениям ортогональности (формула 9.2).В ходе передачи данных (напомним, что хранение в памяти интерпретируется как передача во времени) могут возникнуть ошибки. Удобно представить совокупность ошибок при передачи слова Х как вектор E, содержащий “1” в неверных разрядах.
Тогда принятый кодовый вектор Y в общем случае отличается от переданного.
Декодирование означает проверку правильности вектора Y и исправление ошибки, если она обнаружена.
С этой целью вектор Y {y1…yn} вновь проверяется на ортогональность той же матрице (здесь вектор, если произошла ошибка).
Замечательное свойство кода Хэмминга состоит в том, что по виду вектора Z можно определить не только наличие ошибки, но и номер разряда, в котором она произошла, а значит – исправить ее инвертированием). Напомним, что для исправления однократной ошибки необходимо Именно такое значение обеспечивается за счет выбора m в коде Хемминга.

Дата добавления: 2015-10-23