
Читайте также:
|
ВЫСШАЯ МАТЕМАТИКА
Программа и контрольные задания
Для студентов инженерных специальностей
заочной и вечерней форм обучения
СЕМЕСТР 2
Красноярск 2005
Указания по выполнению контрольных работ
Студент должен выполнять один тот же вариант всех контрольных работ. Чтобы определить свой вариант, нужно разделить на 25 число, полученное отсечением двух цифр от номера студенческого билета (шифра), обозначающих год поступления в университет. Остаток от деления и есть номер вашего варианта. Если остаток равен нулю, то номер вашего варианта равен 25. Например, если шифр студента равен 23602, тогда остаток от деления 236 на 25 будет равен 11 и, следовательно, решать нужно вариант №11; если шифр студента равен 57501, тогда остаток от деления 575 на 25 будет равен 0 и, следовательно, решать нужно вариант №25.
При выполнении контрольных работ необходимо соблюдать следующие правила:
1. В начале работы разборчиво написать свою фамилию, инициалы, шифр, номер и вариант контрольной работы и дату отсылки ее в университет.
2. Каждую контрольную работу выполнять в отдельной тетради (или на белой бумаге формата А4), авторучкой или распечатанной на принтере с полями не менее 3 см для замечаний рецензента.
3. Решения задач располагать в порядке номеров, указанных в контрольных работах. В начале каждого решения записывать условие задачи (без сокращений).
4. Решения задач и объяснения к ним должны быть подробными, аккуратными, без сокращения слов. Обязательно, если требуется, выполнять чертежи с пояснениями и нарисованными аккуратно.
Контрольные работы, выполненные с нарушением изложенных правил или не своего варианта, не засчитываются и возвращаются без проверки.
Получив прорецензированную работу, студент обязан исправить в ней отмеченные ошибки и недочеты. Если работа не зачтена, ее необходимо в короткий срок либо выполнить заново (целиком), либо решить заново задачи, указанные рецензентом. Исправленную работу следует посылать в университет вместе с незачтенной. Зачтенные контрольные работы предъявляются преподавателю при защите перед зачетом или экзаменом.
Программа курса «Высшая математика»
РАЗДЕЛ 1. Интегральное исчисление
1.1 Первообразная. Неопределенный интеграл и его свойства.
1.2 Табличный интеграл. Замена переменной и интегрирование по частям в неопределенном интеграле.
1.3 Многочлены. Теорема Безу. Основная теорема алгебры. Разложение многочлена с действительными коэффициентами на линейные и квадратичные множители.
1.4 Разложение рациональных дробей на простейшие.
1.5 Интегрирование рациональных дробей.
1.6 Интегрирование тригонометрических выражений. Универсальная подстановка.
1.7 Интегрирование некоторых иррациональных и трансцендентных функций.
1.8 Задачи, приводящие к понятию определенного интеграла. Определенный интеграл, его свойства.
1.9 Формула Ньютона-Лейбница, ее применения для вычисления определенных интегралов.
1.10 Геометрические и механические приложения определенного интеграла.
1.11 Несобственные интегралы первого и второго рода, их основные свойства. Признаки сходимости несобственных интегралов. Понятие сингулярных интегралов.
1.12 Двойные и тройные интегралы.
1.13 Криволинейные и поверхностные интегралы.
ЛИТЕРАТУРА
1. Гусак А.А. Высшая математика. В 2-х т.: Учеб. пособие. Мн: ТетраСистемс, 1998.
2. Шипачев В.С. Высшая математика. М: Высш. шк., 2003.
3. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч.1,2. М: Высш. шк., 2003.
4. Письменный Д.Т. Конспект лекций по высшей математике. В 2-х т. М: Айрис-пресс, 2002.
5. Бугров Я.С., Никольский С.М. Высшая математика: В 3-х т. М: Дрофа, 2003.
6. Пискунов Н.С. Дифференциальное и интегральное исчисления: В 2-х т.: Учеб. пособие для втузов. М.: Интеграл-пресс. 2001.
7. Натансон И.П. Краткий курс высшей математики. СПб.: Лань, 2001.
8. Ильин В.А., Позняк Э.Г. Основы математического анализа. В 2-х ч. М.:ФИЗМАТЛИТ. 2001.
КОНТРОЛЬНАЯ РАБОТА №3
(интегральное исчисление)
СЕМЕСТР 2
Вариант 1
1. Вычислить неопределенные интегралы:
а) 
| б) 
| в) 
|
г) 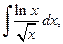
| д) 
| е)  , ,
|
ж).  , ,
| з)  , ,
| и)  . .
|
2. Вычислить определенные интегралы:
а) 
| б) 
| в)  . .
|
3. Вычислить несобственные интегралы:
а) 
| б)  . .
|
4. Найти площадь фигуры, ограниченной линиями. Сделать чертеж.
| а) y = (x– 2)3, y = 4 x –8; | б) r = 4cos3j, | в) 
|
Вариант 2
1. Вычислить неопределенные интегралы:
а) 
| б) 
| в) 
|
г) 
| д) 
| е)  , ,
|
ж).  , ,
| з)  , ,
| и)  . .
|
2. Вычислить определенные интегралы:
а) 
| б) 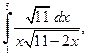
| в)  . .
|
3. Вычислить несобственные интегралы:
а) 
| б)  . .
|
4. Найти площадь фигуры, ограниченной линиями. Сделать чертеж.
| а) y = 4– x 2, y = x 2–2 x, | б)r = cos2j, | в) 
|
Вариант 3
1. Вычислить неопределенные интегралы:
а) 
| б) 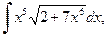
| в) 
|
г) 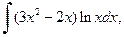
| д) 
| е)  , ,
|
ж).  , ,
| з)  , ,
| и)  . .
|
2. Вычислить определенные интегралы:
а) 
| б) 
| в)  . .
|
3. Вычислить несобственные интегралы:
а) 
| б)  . .
|
4. Найти площадь фигуры, ограниченной линиями. Сделать чертеж.
а) y =  , y = 0, (0£ x £3), , y = 0, (0£ x £3),
| б) r = 4sin3j, | в) 
|
Вариант 4
1. Вычислить неопределенные интегралы:
а) 
| б) 
| в) 
|
г) 
| д) 
| е)  , ,
|
ж). 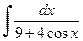 , ,
| з)  , ,
| и)  . .
|
2. Вычислить определенные интегралы:
а) 
| б) 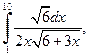
| в)  . .
|
3. Вычислить несобственные интегралы:
а) 
| б)  . .
|
4. Найти площадь фигуры, ограниченной линиями. Сделать чертеж.
| а) y = (x+ 1)2, y 2= x +1, | б) r = 1+cosj, | в) 
|
Вариант 5
1. Вычислить неопределенные интегралы:
а)  , ,
| б)  , ,
| в)  , ,
|
г)  , ,
| д) 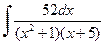 , ,
| е)  , ,
|
ж).  , ,
| з)  , ,
| и)  . .
|
2. Вычислить определенные интегралы:
а) 
| б) 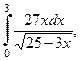
| в)  . .
|
3. Вычислить несобственные интегралы:
а)  , ,
| б)  . .
|
4. Найти площадь фигуры, ограниченной линиями. Сделать чертеж.
| А). y = (x –2)2, y = 4 x –8, | б) r = 1+sinj, | в) 
|
Вариант 6
1. Вычислить неопределенные интегралы:
а) 
| б) 
| в)  , ,
|
г) 
| д) 
| е) 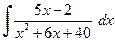 , ,
|
ж).  , ,
| з)  , ,
| и)  . .
|
2. Вычислить определенные интегралы:
а) 
| б) 
| в)  . .
|
3. Вычислить несобственные интегралы:
а)  , ,
| б)  . .
|
4. Найти площадь фигуры, ограниченной линиями. Сделать чертеж.
| а) y = (x –2)2, y = 4 x –8, | б) r = 1+sinj, | в) 
|
Вариант 7
1. Вычислить неопределенные интегралы:
а) 
| б) 
| в) 
|
г) 
| д) 
| е)  , ,
|
ж).  , ,
| з)  , ,
| и)  . .
|
2. Вычислить определенные интегралы:
а) 
| б) 
| в)  . .
|
3. Вычислить несобственные интегралы:
а) 
| б)  . .
|
4. Найти площадь фигуры, ограниченной линиями. Сделать чертеж.
| а) y = (x– 1)2, y 2= x –1, | б) r = sin2j, | в) 
|
Вариант 8
1. Вычислить неопределенные интегралы:
а) 
| б) 
| в)  , ,
|
г) 
| д) 
| е)  , ,
|
ж).  , ,
| з)  , ,
| и)  . .
|
2. Вычислить определенные интегралы:
а) 
| б) 
| в)  . .
|
3. Вычислить несобственные интегралы:
а)  , ,
| б)  . .
|
4. Найти площадь фигуры, ограниченной линиями. Сделать чертеж.
| а) y = 4– x 2, y = x 2–2 y, | б) r = cos2j, | в) 
|
Вариант 9
1. Вычислить неопределенные интегралы:
а) 
| б) 
| в) 
|
г) 
| д) 
| е)  , ,
|
ж).  , ,
| з)  , ,
| и)  . .
|
2. Вычислить определенные интегралы:
а) 
| б) 
| в)  . .
|
3. Вычислить несобственные интегралы:
а)  , ,
| б)  . .
|
4. Найти площадь фигуры, ограниченной линиями. Сделать чертеж.
| а) y = (x– 1)2, y 2= x –1, | б) r = sin2j, | в) 
|
Вариант 10
1. Вычислить неопределенные интегралы:
а) 
| б) 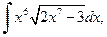
| в)  , ,
|
г) 
| д) 
| е)  , ,
|
ж).  , ,
| з)  , ,
| и)  . .
|
2. Вычислить определенные интегралы:
а) 
| б) 
| в)  . .
|
3. Вычислить несобственные интегралы:
а) 
| б) 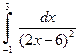 . .
|
4. Найти площадь фигуры, ограниченной линиями. Сделать чертеж.
| а) y = (x +3)3, y = 4 x +12, | б) r = 3cos4j, | в) 
|
Вариант 11
1. Вычислить неопределенные интегралы:
а) 
| б) 
| в) 
|
г) 
| д) 
| е)  , ,
|
ж).  , ,
| з) 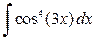 , ,
| и)  . .
|
2. Вычислить определенные интегралы:
а) 
| б) 
| в)  . .
|
3. Вычислить несобственные интегралы:
а)  , ,
| б)  . .
|
4. Найти площадь фигуры, ограниченной линиями. Сделать чертеж.
| а) y = 8– x 2, y = x 2–6 x, | б) r = 3sin4j., | в) 
|
Вариант 12
1. Вычислить неопределенные интегралы:
а) 
| б) 
| в) 
|
г) 
| д) 
| е)  , ,
|
ж).  , ,
| з)  , ,
| и)  . .
|
2. Вычислить определенные интегралы:
а) 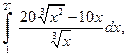
| б) 
| в)  . .
|
3. Вычислить несобственные интегралы:
а) 
| б)  . .
|
4. Найти площадь фигуры, ограниченной линиями. Сделать чертеж.
а) y =  , y = 0, (0£ x £5), , y = 0, (0£ x £5),
| б) r = 1+sin2j, | в) 
|
Вариант 13
1. Вычислить неопределенные интегралы:
а) 
| б) 
| в) 
|
г) 
| д) 
| е)  , ,
|
ж).  , ,
| з)  , ,
| и)  . .
|
2. Вычислить определенные интегралы:
а) 
| б) 
| в)  . .
|
3. Вычислить несобственные интегралы:
а) 
| б) 
|
4. Найти площадь фигуры, ограниченной линиями. Сделать чертеж.
| а) y = (x –2)2, y 2= x –2, | б) r = 1+cos2j, | в) 
|
Вариант 14
1. Вычислить неопределенные интегралы:
а) 
| б) 
| в) 
|
г) 
| д) 
| е) 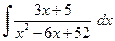 , ,
|
ж).  , ,
| з)  , ,
| и)  . .
|
2. Вычислить определенные интегралы:
а) 
| б) 
| в)  . .
|
3. Вычислить несобственные интегралы:
а) 
| б)  . .
|
4. Найти площадь фигуры, ограниченной линиями. Сделать чертеж.
| а) y = (x –3)2, y = 4 x –12, | б) r = 2(1–sinj), | в) 
|
Вариант 15
1. Вычислить неопределенные интегралы:
а)  , ,
| б) 
| в)  , ,
|
г) 
| д) 
| е)  , ,
|
ж).  , ,
| з)  , ,
| и)  . .
|
2. Вычислить определенные интегралы:
а) 
| б) 
| в)  . .
|
3. Вычислить несобственные интегралы:
а)  , ,
| б)  . .
|
4. Найти площадь фигуры, ограниченной линиями. Сделать чертеж.
а) y =  , y = 0, (0£ x £4), , y = 0, (0£ x £4),
| б) r = 1+sin2j, | в) 
|
Вариант 16
1. Вычислить неопределенные интегралы:
а) 
| б) 
| в)  , ,
|
г) 
| д) 
| е)  , ,
|
ж).  , ,
| з)  , ,
| и) 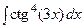 . .
|
2. Вычислить определенные интегралы:
а) 
| б) 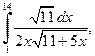
| в)  . .
|
3. Вычислить несобственные интегралы:
а)  , ,
| б) 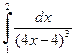 . .
|
4. Найти площадь фигуры, ограниченной линиями. Сделать чертеж.
| а) y = (x– 2)2, y 2= x –2, | б) r = 2(1–cosj), | в) 
|
Вариант 17
1. Вычислить неопределенные интегралы:
а) 
| б) 
| в) 
|
г) 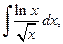
| д) 
| е)  , ,
|
ж).  , ,
| з)  , ,
| и) 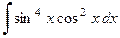 . .
|
2. Вычислить определенные интегралы:
а) 
| б) 
| в)  . .
|
3. Вычислить несобственные интегралы:
а) 
| б) 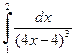 . .
|
4. Найти площадь фигуры, ограниченной линиями. Сделать чертеж.
| а) y = (x– 2)2, y 2= x –2, | б) r = 2(1–cosj), | в) 
|
Вариант 18
1. Вычислить неопределенные интегралы:
а) 
| б) 
| в) 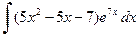 , ,
|
г) 
| д) 
| е)  , ,
|
ж).  , ,
| з)  , ,
| и)  . .
|
2. Вычислить определенные интегралы:
а) 
| б) 
| в)  . .
|
3. Вычислить несобственные интегралы:
а) 
| б)  . .
|
4. Найти площадь фигуры, ограниченной линиями. Сделать чертеж.
| а) y = 7– x 2, y = x 2–6 x +11, | б) r = –6sin4j, | в) 
|
Вариант 19
1. Вычислить неопределенные интегралы:
а) 
| б) 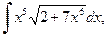
| в) 
|
г) 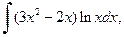
| д) 
| е)  , ,
|
ж).  , ,
| з)  , ,
| и)  . .
|
2. Вычислить определенные интегралы:
а) 
| б) 
| в)  . .
|
3. Вычислить несобственные интегралы:
а)  , ,
| б)  . .
|
4. Найти площадь фигуры, ограниченной линиями. Сделать чертеж.
| а) y = (x+ 3)3, y = 4 x +12, | б) r = –6cos4j, | в) 
|
Вариант 20
1. Вычислить неопределенные интегралы:
а) 
| б) 
| в)  , ,
|
г) 
| д) 
| е)  , ,
|
ж).  , ,
| з)  , ,
| и) 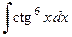 . .
|
2. Вычислить определенные интегралы:
а) 
| б) 
| в) 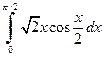 . .
|
3. Вычислить несобственные интегралы:
а) 
| б)  . .
|
4. Найти площадь фигуры, ограниченной линиями. Сделать чертеж.
| а) y = 9– x 2, y = x 2–4 x +9, | б) r = –2cos3j, | в) 
|
Вариант 21
1. Вычислить неопределенные интегралы:
а) 
| б) 
| в) 
|
г) 
| д) 
| е)  , ,
|
ж).  , ,
| з)  , ,
| и)  . .
|
2. Вычислить определенные интегралы:
а) 
| б) 
| в)  . .
|
3. Вычислить несобственные интегралы:
а) 
| б) 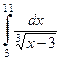 . .
|
4. Найти площадь фигуры, ограниченной линиями. Сделать чертеж.
а) y = 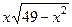 , y = 0, (0£ x £7), , y = 0, (0£ x £7),
| б) r = –2sin3j, | в) 
|
Вариант 22
1. Вычислить неопределенные интегралы:
а) 
| б) 
| в) 
|
г) 
| д) 
| е)  , ,
|
ж).  , ,
| з)  , ,
| и)  . .
|
2. Вычислить определенные интегралы:
а) 
| б) 
| в)  . .
|
3. Вычислить несобственные интегралы:
а) 
| б)  . .
|
4. Найти площадь фигуры, ограниченной линиями. Сделать чертеж.
| а) y = (x –3)2, y 2= x –3, | б) r = cosj+1, | в) 
|
Вариант 23
1. Вычислить неопределенные интегралы:
а) 
| б) 
| в) 
|
г) 
| д) 
| е) 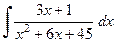 , ,
|
ж).  , ,
| з)  , ,
| и)  . .
|
2. Вычислить определенные интегралы:
а) 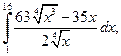
| б) 
| в)  . .
|
3. Вычислить несобственные интегралы:
а) 
| б)  . .
|
4. Найти площадь фигуры, ограниченной линиями. Сделать чертеж.
| а) y = (x –3)2, y 2= x –3; | б) r = cosj+1, | в) 
|
Вариант 24
1. Вычислить неопределенные интегралы:
а) 
| б) 
| в) 
|
г) 
| д) 
| е)  , ,
|
ж).  , ,
| з)  , ,
| и)  . .
|
2. Вычислить определенные интегралы:
а) 
| б) 
| в)  . .
|
3. Вычислить несобственные интегралы:
а) 
| б)  . .
|
4. Найти площадь фигуры, ограниченной линиями. Сделать чертеж.
| а) y = 4– x 2, y = x 2–2 x, | б) r = cos2j, | в) 
|
Вариант 25
1. Вычислить неопределенные интегралы:
а)  , ,
| б)  , ,
| в)  , ,
|
г) 
| д) 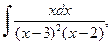
| е)  , ,
|
ж).  , ,
| з)  , ,
| и)  . .
|
2. Вычислить определенные интегралы:
а) 
| б) 
| в) 
|
3. Вычислить несобственные интегралы:
а) 
| б) 
|
4. Найти площадь фигуры, ограниченной линиями. Сделать чертеж.
| а) y = (x– 3)2, y 2= 5 x –9, | б) r = cos2j+1, | в) 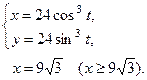
|
Вопросы к защите контрольных работ
и для подготовки к экзаменам
СЕМЕСТР 2
Дата добавления: 2015-10-30; просмотров: 72 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Character traits | | | Chapters 14, Ex.5,6 p.269, 7 p.270, 11 p.270, 15, 16, 17 p.273. |