Проверка зубьев передачи на изгиб

Введение

Инженер-конструктор является творцом новой техники, и уровнем его творческой работы в большей степени определяются темпы научно-технического прогресса. Деятельность конструктора принадлежит к числу наиболее сложных проявлений человеческого разума. Решающая роль успеха при создании новой техники определяется тем, что заложено на чертеже конструктора. С развитием науки и техники проблемные вопросы решаются с учетом все возрастающего числа факторов, базирующихся на данных различных наук. При выполнении проекта используются математические модели, базирующиеся на теоретических и экспериментальных исследованиях, относящихся к объемной и контактной прочности, материаловедению, теплотехнике, гидравлике, теории упругости, строительной механике. Широко используются сведения из курсов сопротивления материалов, теоретической механики, машиностроительного черчения и т. д. Все это способствует развитию самостоятельности и творческого подхода к поставленным проблемам.

При выборе типа редуктора для привода рабочего органа (устройства) необходимо учитывать множество факторов, важнейшими из которых являются: значение и характер изменения нагрузки, требуемая долговечность, надежность, КПД, масса и габаритные размеры, требования к уровню шума, стоимость изделия, эксплуатационные расходы.

Из всех видов передач зубчатые передачи имеют наименьшие габариты, массу, стоимость и потери на трение. Коэффициент потерь одной зубчатой пары при тщательном выполнении и надлежащей смазке не превышает обычно 0,01. Зубчатые передачи в сравнении с другими механическими передачами обладают большой надежностью в работе, постоянством передаточного отношения из-за отсутствия проскальзывания, возможностью применения в широком диапазоне скоростей и передаточных отношений. Эти свойства обеспечили большое распространение зубчатых передач; они применяются для мощностей, начиная от ничтожно малых (в приборах) до измеряемых десятками тысяч киловатт.

К недостаткам зубчатых передач могут быть отнесены требования высокой точности изготовления и шум при работе со значительными скоростями.

Косозубые колеса применяют для ответственных передач при средних и высоких скоростях. Объем их применения - свыше 30% объема применения всех цилиндрических колес в машинах; и этот процент непрерывно возрастает. Косозубые колеса с твердыми поверхностями зубьев требуют повышенной защиты от загрязнений во избежание неравномерного износа по длине контактных линий и опасности выкрашивания.

Одной из целей выполненного проекта является развитие инженерного мышления, в том числе умение использовать предшествующий опыт, моделировать используя аналоги. Для курсового проекта предпочтительны объекты, которые не только хорошо распространены и имеют большое практическое значение, но и не подвержены в обозримом будущем моральному старению.

Существуют различные типы механических передач: цилиндрические и конические, с прямыми зубьями и косозубые, гипоидные, червячные, глобоидные, одно- и многопоточные и т. д. Это рождает вопрос о выборе наиболее рационального варианта передачи. При выборе типа передачи руководствуются показателями, среди которых основными являются КПД, габаритные размеры, масса, плавность работы и вибронагруженность, технологические требования, предпочитаемое количество изделий.

При выборе типов передач, вида зацепления, механических характеристик материалов необходимо учитывать, что затраты на материалы составляют значительную часть стоимости изделия: в редукторах общего назначения - 85%, в дорожных машинах - 75%, в автомобилях - 10% и т. д.

Поиск путей снижения массы проектируемых объектов является важнейшей предпосылкой дальнейшего прогресса, необходимым условием сбережения природных ресурсов. Большая часть вырабатываемой в настоящее время энергии приходится на механические передачи, поэтому их КПД в известной степени определяет эксплуатационные расходы.

Наиболее полно требования снижения массы и габаритных размеров удовлетворяет привод с использованием электродвигателя и редуктора с внешним зацеплением.

2 Выбор электродвигателя и кинематический расчёт

По табл. 1.1[1] примем следующие значения КПД:

- для ременной передачи с плоским ремнем: h1= 0,97

- для закрытой зубчатой цилиндрической передачи: h2= 0,975

Общий КПД привода вычисляем по формуле:

h = h1· h2· hподш.2 (2.1)

где hподш.= 0,99 - КПД одной пары подшипников.

Подставляя, получим:

h = 0,97 · 0,975 · 0,992= 0,927

Требуемая мощность двигателя будет:

Pтреб.= (2.2)

После подстановки имеем:

Pтреб.= = 5,394 кВт

В таблице П.1[1](см. приложение) по требуемой мощности выбираем электродвигатель 132S2, с синхронной частотой вращения nдвиг.синх.=1000 об/мин, с параметрами: Pдвиг.=5,5 кВт и скольжением s=3,3% (ГОСТ 19523-81). Номинальная частота вращения с учётом скольжения:

nдвиг.= nдвиг.синх.- (2.3)

Подставляя соответствующие значения, получаем:

nдвиг.= 1000 - = 967 об/мин,

Угловая скорость:

wдвиг.= (2.4)

В итоге получаем:

wдвиг.= = 101,264 рад/с.

Oбщее передаточное отношение:

uобщ.= (2.5)

После подстановки получаем:

uобщ.= = 9,481

Для передач выбрали следующие передаточные числа:

u1= 2,3

u2= 4

Рассчитанные частоты и угловые скорости вращения валов сведены ниже в таблицу.

Таблица 1. Частоты и угловые скорости вращения валов.

Вал	Частота вращения, об./мин	Угловая скорость вращения, рад/с
Вал 1-й	n1= = = 420,435	w1= = = 44,028
Вал 2-й	n2= = = 105,109	w2= = = 11,007

Мощности на валах:

Pведущ.шкив.1-й передачи= Pтреб.= 5394Вт

P1= Pтреб.· h1· hподш.= 5394 · 0,97 · 0,99 = 5179,858 Вт

P2= P1· h2· hподш.= 5179,858 · 0,975 · 0,99 = 4999,858 Вт

Вращающие моменты на валах:

Tведущ.шкив.1-й передачи= = = 53266,709 H·мм = 53,267 H·м

T1= = = 117649,178 Н·мм = 117,649 Н·м

T2= = = 454243,481 Н·мм = 454,243 Н·м

По таблице П.1(см. приложение учебника Чернавского) выбран электродвигатель 132S2, с синхронной частотой вращения 1000 об/мин, с мощностью Pдвиг.=5,5 кВт и скольжением 3,3% (ГОСТ 19523-81). Номинальная частота вращения с учётом скольжения nдвиг.= 967 об/мин.

Таблица 2. Передаточные числа и КПД передач.

Передачи	Передаточное число	КПД
1-я ременная передача с плоским ремнём	2,3	0,97
2-я закрытая зубчатая цилиндрическая передача		0,975

Таблица 3. Рассчитанные частоты, угловые скорости вращения валов и моменты на валах.

Валы	Частота вращения, об/мин	Угловая скорость, рад/мин	Момент, Нxмм
1-й вал	420,435	44,028	117649,178
2-й вал	105,109	11,007	454243,481

7 Расчёт 1-й плоскоременной передачи

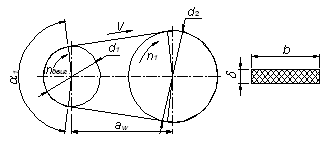
Рис. 1. Передача плоскоременная.

1. Вращающий момент и мощность на ведущем шкиве:

T(ведущий шкив)= 53266,709 Н·мм.

здесь T(ведущий шкив)= T(двиг.)= = = 53266,709 Н·мм.

P = T(ведущий шкив)· w(двиг.)= 53266,709 · 10-6· 101,264 = 5,394кВт (7.1)

2. Диаметр ведущего шкива d1по формуле 7.2[1]:

d1= 6 · 6 · 225,755 мм. (7.2)

Принимаем из стандартного ряда: d1= 224 мм.

3. Диаметр ведомого шкива d2вычислим c учетом относительного скольжения ремня e=0,015 по формуле 7.3[1]:

d2= d1· u1· (1 - e) = 224 · 2,3 · (1 - 0,015) = 507,472 мм. (7.3)

Принимаем из стандартного ряда: d2= 500 мм.

4. Передаточное отношение рассчитаем по формуле 7.3[1]:

uр= 2,266 (7.4)

При этом угловая скорость ведомого шкива будет:

w(ведомый шкив)p= 44,688 рад/с. (7.5)

что допустимо:

100% · 100% · -1,499% (отклонение не должно превышать 3%).

5. Межосевое расстояние находим по формуле 7.5[1]:

aw= 2 · (d1+ d2) = 2 · (224 + 500) = 1448 мм. (7.6)

6. Угол обхвата малого шкива вычисляется по формуле 7.6[1]:

a1= 180o- 60 · 180o- 60 · 168,564o (7.7)

7. Длина ремня (без учета припуска на соединение концов):

L = 2 · aw+ 0.5 · p · (d1+ d2) + (7.8)

L = 2 · 1448 + 0.5 · 3,142 · (224 + 500) + = 4033,304 мм.

Принимаем L = 4033 мм.

8. Расчетная скорость ремня (формула 7.8[1]):

V = (7.9)

V = = 11,342 м/c.

9. Окружную силу находим по формуле 7.9[1]:

Ft= 475,577 H (7.10)

Из 7.1[1] выбираем резинотканевый ремень Б-800 c числом прокладок z=3, толщиной прокладки d0= 1,5 мм, толщиной ремня d = z · d0= 4,5 мм, наибольшей допускаемой нагрузкой р0= 3 H/мм.

Проверяем выполнение условия достаточной эластичности ремня:

d £ 0.025 · d1= 0.025 · 224 = 5,6 мм. (7.11)

10. Коэффициент угла обхвата (формула 7.14[1]):

Сa= 1 - 0.003 · (180o- a1) = 1 - 0.003 · (180o- 168,564) = 0,966. (7.12)

11. Коэффициент, учитывающий влияние скорости ремня (по формуле 7.15[1]):

Cv= 1.04 - 0.0004 · V2= 1.04 - 0.0004 · 11,3422= 0,989. (7.13)

12. Коэффициент, учитывающий режим работы равен (по табл. 7.5[1]): Cр= 0,8.

13. Коэффициент, учитывающий угол наклона линии центров передачи к линии горизонта:до 60oпринимаем: Сq= 1.

14. Допускаемая нагрузка на 1 мм ширины прокладки (формула 7.13[1]):

[P0] = p0· Ca· Cv· Cр· Cq= 3 · 0,966 · 0,989 · 0,8 · 1 = 2,293 Н/мм. (7.14)

15. Ширина ремня равна по формуле 7.12[1]:

b ³69,135 мм (7.15)

Принимаем по таблице 7.2[1]: b = 71 мм.

16. Предварительное натяжение ремня (формула 7.11[1]):

F0= s0· b · d = 1.8 · 71 · 4,5 = 575,1 H, (7.16)

где s0= 1.8 МПа - напряжение от предварительного натяжения.

17. Натяжение ветвей по формулам 7.10[1]:

ведомой: F1= F0+ 0.5 · Ft= 575,1 + 0.5 · 475,577 = 812,888 H, (7.17)

ведущей: F2= F0- 0.5 · Ft= 575,1 - 0.5 · 475,577 = 337,312 H. (7.18)

18. Напряжение от силы F1находим по формуле 7.19[1]:

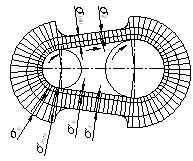
Рис. 2. Эпюра суммарных напряжений ремня.

s1= 2,544 МПа (7.19)

19. Напряжение изгиба (формулa 7.19[1]):

sи= 2,009 МПа. (7.20)

где Еи= 100 МПа - для резинотканевых ремней.

20. Напряжение от центробежных сил (по формуле 7.19[1]):

sv= r · V2· 10-6= = 1200 · 11,3422· 10-6= 0,154 МПа. (7.21)

где r = 1200 кг/м3- плотность ремня.

21. Максимальное напряжение по формуле 7.18[1] будет:

smax= s1+ sи+ sv= 2,544 + 2,009 + 0,154 = 4,707 МПа (7.22)

Условие прочности smax£ 7 МПа выполнено.

22. Проверка долговечности ремня:

а) число пробегов:

l = 2,812; (7.23)

б) коэффициент, учитывающий влияние передаточного отношения;

Ci= 1.5 · - 0.5 = 1.5 · - 0.5 = 1,47; (7.24)

в) коэффициент, учитывающий характер нагрузки СH= 1 при постоянной нагрузке.

Находим долговечность ремня по формуле 7.22[1]

H0= (7.25)

H0= = 7854,03 ч.

Долговечность ремня не должна быть меньше 2000 ч.

Условие долговечности Н0³ 2000 ч выполнено.

23. Нагрузка на валы передачи находится по формуле 7.23[1]:

Fв= 3 · F0· sin3 · 575,1 · sin1716,715 H. (7.26)

24. Ширина шкива выбирается по табл. 7.6[1]: В = 80 мм.

Таблица 4. Параметры плоскоременной передачи, мм.

Параметр	Значение	Параметр	Значение
Тип ремня	резинотканиевый	Диаметр ведущего шкива d1
Межосевое расстояние aw		Диаметр ведомого шкива d2
Толщина ремня d	4,5	Максимальное напряжение smax, H/мм2	4,707
Ширина ремня b
Длина ремня l		Предварительное натяжение ремня Fo, Н	575,1
Угол обхвата ведущего шкива a1, град	168,564	Сила давления ремня на вал Fв, Н	1716,715

3 Расчёт зубчатой цилиндрической передачи

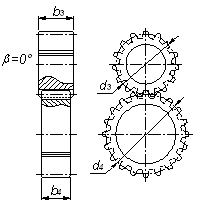
Рис. 3. Передача зубчатая цилиндрическая прямозубая.

3.1 Проектный расчёт

Так как в задании нет особых требований в отношении габаритов передачи, выбираем материалы со средними механическими характеристиками (см. гл.3, табл. 3.3[1]):

- для шестерни:

сталь: 40ХН

термическая обработка: улучшение

твердость: HB 280

- для колеса:

сталь: 40ХН

термическая обработка: улучшение

твердость: HB 265

Допустимые контактные напряжения (формула (3.9)[1]), будут:

[sH] = (3.1)

По таблице 3.2 гл. 3[1] имеем для сталей с твердостью поверхностей зубьев менее HB 350:

sH lim b= 2 · HB + 70 (3.2)

sH lim b (шестерня)= 2 · 280 + 70 = 630 МПа;

sH lim b (колесо)= 2 · 265 + 70 = 600 МПа;

KHL- коэффициент долговечности; при числе циклов нагружения больше базового, что имеет место при длительной эксплуатации редуктора, принимаем KHL= 1; коэффициент безопасности [SH]=1,1.

Допустимые контактные напряжения:

для шестерни [ sH3] = = 572,727 МПа;

для колеса [ sH4] = = 545,455 МПа.

Для прямозубых колес за расчетное напряжение принимается минимальное допустимое контактное напряжение шестерни или колеса.

Тогда расчетное допускаемое контактное напряжение будет:

[ sH] = [ sH4] = 545,455 МПа.

Принимаем коэффициент симметричности расположения колес относительно опор по таблице 3.5[1]: KHb= 1,15.

Коэффициент ширины венца по межосевому расстоянию принимаем: yba= = 0,25, (см. стр.36[1]).

Межосевое расстояние из условия контактной выносливости активных поверхностей зубьев найдем по формуле 3.7 гл. 3[1]:

aw= Ka· (u2+ 1) · (3.3)

aw= 49.5 · (4 + 1) · = 188,095 мм.

где для прямозубых колес Кa= 49,5, передаточное число передачи u2= 4; T2= 454243,481 Н·мм - вращающий момент на колесе.

Принимаем значение межосевого расстояния по ГОСТ 2185-66: aw= 180 мм.

Нормальный модуль зацепления берем по следующей рекомендации:

mn= (0.01...0.02) · awмм, для нас: mn= 1,8...3,6 мм, принимаем:

по ГОСТ 9563-60* (см. стр. 36[1]) mn= 2 мм.

Задаемся суммой зубьев:

SZ = z3+ z4= = = 180

Числа зубьев шестерни и колеса:

z3= = = 36 (3.4)

z4= SZ - z3= 180 - 36 = 144 (3.5)

Угол наклона зубьев b = 0o.

Основные размеры шестерни и колеса:

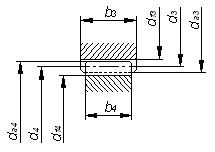
Рис. 4. Зацепление зубчатой цилиндрической передачи.

диаметры делительные:

d = (3.6)

d3= = = 72 мм;

d4= = = 288 мм.

Проверка: aw = = = 180 мм.

диаметры вершин зубьев:

da= d + 2 · mn (3.7)

da3= d3+ 2 · mn= 72 + 2 · 2 = 76 мм;

da4= d4+ 2 · mn= 288 + 2 · 2 = 292 мм.

ширина колеса: b4= yba· aw= 0,25 · 180 = 45 мм; (3.8)

ширина шестерни: b3= b4+ 5 = 45 + 5 = 50 мм; (3.9)

Определим коэффициент ширины шестерни по диаметру:

ybd= = = 0,694 (3.10)

Окружная скорость колес будет:

V = = = 1,585 м/c; (3.11)

При такой скорости следует принять для зубчатых колес 8-ю степень точности.

Коэффициент нагрузки равен:

KH= KHb· KHa· KHn. (3.12)

Коэффициент KHb=1,025 выбираем по таблице 3.5[1], коэффициент KHa=1 выбираем по таблице 3.4[1], коэффициент KHn=1,05 выбираем по таблице 3.6[1], тогда:

KH= 1,025 · 1 · 1,05 = 1,076

3.1 Проверочный расчёт по контактным напряжениям

Проверку контактных напряжений проводим по формуле 3.6[1]:

sH= (3.13)

sH = =

= 501,682 МПа. £ [sH]

Фактическая недогрузка:

DsH= = = -8,025%, что меньше допустимых 13%.

Силы действующие в зацеплении вычислим по формуле 8.3 и 8.4[1]:

окружная:

Ft3= Ft4= = = 3268,033 Н, (3.14)

радиальная:

Fr3= Fr4= Ft3· = 3268,033 · = 1189,467 Н; (4.15)

осевая:

Fa3= Fa4= F t3· tg(b) = 3268,033 · tg(0o) = 0 Н. (3.16)

Проверка зубьев передачи на изгиб

Проверим зубья на выносливость по напряжениям изгиба по формуле 3.22[1]:

sF= £ [sF] (3.17)

Здесь коэффициент нагрузки KF= KFb· KFn(см. стр. 42[1]). По таблице 3.7[1] выбираем коэффициент расположения колес KFb= 1,064, по таблице 3.8[1] выбираем коэффициент KFn=1,25. Таким образом коэффициент KF= 1,064 · 1,25 = 1,33. Y - коэффициент, учитывающий форму зуба и зависящий от эквивалентного числа Zv(см. гл.3, пояснения к формуле 3.25[1]):

у шестерни: Zv3= = = 36 (3.18)

у колеса: Zv4= = = 144 (3.19)

Тогда: YF3= 3,8; YF4= 3,578

Допускаемые напряжения находим по формуле 3.24[1]:

[sF] =. (3.20)

KFL- коэффициент долговечности; при числе циклов нагружения больше базового, что имеет место при длительной эксплуатации редуктора, принимаем KFL= 1.

Для шестерни: soF lim b= 504 МПа;

Для колеса: soF lim b= 477 МПа.

Коэффициент [SF] безопасности находим по формуле 3.24[1]:

[SF] = [SF]' · [SF]". (3.21)

где для шестерни [SF]' = 1,75;

[SF]" = 1;

[SF(шест.)] = 1,75 · 1 = 1,75

для колеса [SF]' = 1,75;

[SF]" = 1.

[SF(кол.)] = 1,75 · 1 = 1,75

Допускаемые напряжения:

для шестерни: [sF3] = = 288 МПа;

для колеса: [sF4] = = 272,571 МПа;

Находим отношения: (3.22)

для шестерни: = = 75,789

для колеса: = = 76,18

Дальнейший расчет будем вести для шестерни, для которой найденное отношение меньше.

Проверяем прочность зуба шестерни:

sF3= = = 165,166 МПа

sF3= 165,166 МПа < [sf] = 272,571 МПа.

Условие прочности выполнено.

Таблица 5. Механические характеристики материалов зубчатой передачи.

Элемент передачи	Марка стали	Термообработка	HB1ср	sв	[s]H	[s]F
HB2ср	H/мм2
Шестерня	40ХН	улучшение			572,727
Колесо	40ХН	улучшение			545,455	272,571

Таблица 6. Параметры зубчатой цилиндрической передачи, мм.

Проектный расчёт
Параметр	Значение	Параметр	Значение
Межосевое расстояние aw		Угол наклона зубьев b, град
Модуль зацепления m		Диаметр делительной окружности:
Ширина зубчатого венца:		шестерни d1 колеса d2
шестерни b1 колеса b2
Числа зубьев:		Диаметр окружности вершин:
шестерни z1 колеса z2		шестерни da1 колеса da2
Вид зубьев	прямозубая передача	Диаметр окружности впадин:
шестерни df1 колеса df2
Проверочный расчёт
Параметр	Допускаемые значения	Расчётные значения	Примечание
Контактные напряжения sH, H/мм2	545,455	501,682	-
Напряжения изгиба, H/мм2	sF1		165,166	-
sF2	272,571	172,797	-

4 Предварительный расчёт валов

Предварительный расчёт валов проведём на кручение по пониженным допускаемым напряжениям.

Диаметр вала при допускаемом напряжении [tк] = 20 МПа вычисляем по формуле 8.16[1]:

dв³ (4.1)

Ведущий вал.

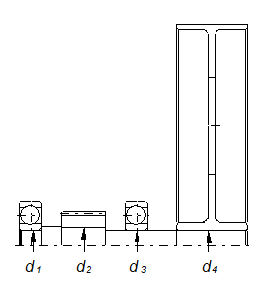
Рис. 5. 1-й вал привода.

dв ³ = 31,058 мм.

Под 1-й элемент (подшипник) выбираем диаметр вала: d1= 35 мм.

Под 2-й элемент (ведущий) выбираем диаметр вала: d2= 40 мм.

Под 3-й элемент (подшипник) выбираем диаметр вала: d3= 35 мм.

Под 4-й элемент (ведомый) выбираем диаметр вала: d4= 34 мм.

Дата добавления: 2015-10-30