
|
Читайте также: |
INTEGRAL 1
1. f(x)=  функциясы үшін алғашқы функцияның жалпы түрін табыңыз:
функциясы үшін алғашқы функцияның жалпы түрін табыңыз:
A) -  +C
+C
B) 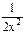 +cosx+C
+cosx+C
C)  +cosx+sinx+C
+cosx+sinx+C
D)  +C
+C
E) -  +
+  +C.
+C.
2. f(x)=x(1-  ) функциясы үшін алғашқы функцияның жалпы түрін табыңыз:
) функциясы үшін алғашқы функцияның жалпы түрін табыңыз:
A)  -
- 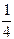 sin4x+C
sin4x+C
B)  -
-  cos4x+C
cos4x+C
C) 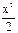 -cos4x+C
-cos4x+C
D)  -4sin4x+C.
-4sin4x+C.
E)  -sin4x+C.
-sin4x+C.
3. f(x) = cos5xcos2x + sіn5xsіn2x функциясының алғашқы функциясын табыңыз.
A) 3sіn3x + C.
B) 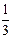 cos3x + C.
cos3x + C.
C)  sіn3x + C.
sіn3x + C.
D) -  sіn3x + C.
sіn3x + C.
E) -  cos3x + C.
cos3x + C.
4. f(x) = 2(2x + 5)4 функциясының алғашқы функциясын табыңыз.
A) 4(2x + 5)3 + C.
B) 8(2x + 5)3 + C.
C)  (2x + 5)5 + C.
(2x + 5)5 + C.
D) 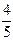 (2x + 5)5 + C.
(2x + 5)5 + C.
E)  (2x + 5)5 + C.
(2x + 5)5 + C.
5. 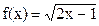 функциясының (0,5; +¥) аралығындағы алғашқы функцияның жалпы түрін табыңыз.
функциясының (0,5; +¥) аралығындағы алғашқы функцияның жалпы түрін табыңыз.
A)  .
.
B)  .
.
C)  .
.
D)  .
.
E)  .
.
6. f(x) =  sіn
sіn  +
+  cos
cos  функцияның алғашқы функциясын табыңыз.
функцияның алғашқы функциясын табыңыз.
A) -  cos
cos  -
-  sіn
sіn  + C
+ C
B) cos  + sіn
+ sіn  + C
+ C
C)  cosx +
cosx +  sіnx + C
sіnx + C
D) -cos  - sіn
- sіn  + C
+ C
E) -cos  + sіn
+ sіn  + C
+ C
7.  функциясының (-0,5; +¥) аралығындағы алғашқы функцияның жалпы түрін табыңыз.
функциясының (-0,5; +¥) аралығындағы алғашқы функцияның жалпы түрін табыңыз.
A)  .
.
B)  .
.
C) 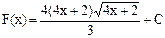 .
.
D) 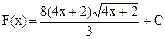 .
.
E)  .
.
8. f(x)=cos  3x-sin
3x-sin  3x функциясы үшін алғашқы функцияның жалпы түрін табыңыз:
3x функциясы үшін алғашқы функцияның жалпы түрін табыңыз:
A) - 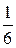 cos6x+C
cos6x+C
B) sin6x+C
C) 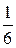 sin6x+C
sin6x+C
D) 6cos6x+C
E) 6sin6x+C
9. f(x)=  (
( +
+  +1) функциясы үшін алғашқы функцияның жалпы түрін табыңыз:
+1) функциясы үшін алғашқы функцияның жалпы түрін табыңыз:
A)  +x
+x  +
+  +C
+C
B)  -6x
-6x  +
+  +C
+C
C)  +
+  x
x  +
+ 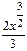 +C
+C
D) 
E) 
10. f(x) = cos5xcos2x + sіn5xsіn2x функциясының алғашқы функциясын табыңыз.
A)  cos3x + C.
cos3x + C.
B) -  sіn3x + C.
sіn3x + C.
C) -  cos3x + C.
cos3x + C.
D) 3sіn3x + C.
E)  sіn3x + C.
sіn3x + C.
11.  функциясының (0,5; +¥) аралығындағы алғашқы функцияның жалпы түрін табыңыз.
функциясының (0,5; +¥) аралығындағы алғашқы функцияның жалпы түрін табыңыз.
A)  .
.
B)  .
.
C)  .
.
D) 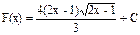 .
.
E)  .
.
12. f(x)= 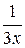 -
-  функциясы үшін алғашқы функцияның жалпы түрін тап:
функциясы үшін алғашқы функцияның жалпы түрін тап:
A)  ln
ln  -x
-x  +C
+C
B) ln  -7x
-7x  +C.
+C.
C)  ln
ln  -7x
-7x  +C
+C
D)  ln
ln  +6x
+6x  +C
+C
E) ln  +7x
+7x  +C
+C
13. f(x) = cosx + cos(-x) функциясының алғашқы функциясын табыңыз.
A) -2sіnx + C.
B) x + C.
C) 2sіnx + C.
D) C.
E) -2cosx + C.
14. f(x)= cos  x +sin
x +sin  x-5cos5x функциясы үшін алғашқы функцияның жалпы түрін тап:
x-5cos5x функциясы үшін алғашқы функцияның жалпы түрін тап:
A) x+cos5x+C
B) x+5sin5x+C
C) x-5cos5x+C
D) x+5cos5x+C
E) x-sin5x+C
15. f(x) =  + x функциясының алғашқы функциясын табыңыз.
+ x функциясының алғашқы функциясын табыңыз.
A) - 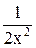 +
+  + C.
+ C.
B)  + х2 + C.
+ х2 + C.
C) 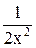 - х2 + C.
- х2 + C.
D)  +
+  + C.
+ C.
E)  +
+ 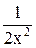 + C.
+ C.
16. f(x) = 3e3x функциясының алғашқы функциясын табыңыз.
A) e3x + C.
B) 9e3x + C.
C) 27e3x + C.
D)  e3x + C.
e3x + C.
E) 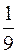 e3x + C.
e3x + C.
17. f(x)=  функциясы үшін алғашқы функцияның жалпы түрін тап:
функциясы үшін алғашқы функцияның жалпы түрін тап:
A) ln  +C.
+C.
B) 8ln  +C
+C
C) 8ln  +C
+C
D) 2ln  +C
+C
E) ln 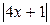 +C
+C
18. f(x) = 6x2 - 3x - 2,5.
F(-1) = 3. F(-2)-ні табыңыз.
A) -18.
B) -13.
C) -15.
D) -27.
E) -23.
19. f(x) = cos2  + sіn2
+ sіn2  функциясының алғашқы функциясын табыңыз.
функциясының алғашқы функциясын табыңыз.
A) x + C.
B) 2x + C.
C) -x + C.
D) sіnx + C.
E)  + C.
+ C.
INTEGRAL 2
1. f(x) = 2sіnx + 3cosx функциясының алғашқы функциясын табыңыз.
A) 2cosx + 3sіnx + C
B) -  cosx +
cosx +  sіnx + C
sіnx + C
C) -2cosx + 3sіnx + C
D) 2cosx - 3sіnx + C
E) -2cosx - 3sіnx + C
2. f(x) =  функциясының алғашқы функциясын табыңыз.
функциясының алғашқы функциясын табыңыз.
A) -3tgx + C.
B) 3tgx + C.
C) -  tgx + C.
tgx + C.
D)  tgx + C.
tgx + C.
E) -  ctgx + C.
ctgx + C.
3. y = x3 +  функцияның алғашқы функциясын табыңыз.
функцияның алғашқы функциясын табыңыз.
A)  -
-  + C
+ C
B)  -
-  + C
+ C
C)  -
-  + C
+ C
D)  +
+  + C
+ C
E) -  -
-  + C
+ C
4. f(x)=cos  3x-sin
3x-sin  3x функциясы үшін алғашқы функцияның жалпы түрін тап:
3x функциясы үшін алғашқы функцияның жалпы түрін тап:
A) 6cos6x+C
B) 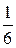 sin6x+C
sin6x+C
C) 6sin6x+C
D) - 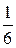 cos6x+C
cos6x+C
E) sin6x+C
5.  функциясы үшін алғашқы функцияның жалпы түрін табыңыз.
функциясы үшін алғашқы функцияның жалпы түрін табыңыз.
A)  .
.
B)  .
.
C)  .
.
D)  .
.
E)  .
.
6.  функциясы үшін алғашқы функцияның жалпы түрін табыңыз.
функциясы үшін алғашқы функцияның жалпы түрін табыңыз.
A)  .
.
B)  .
.
C)  .
.
D) 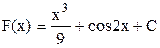 .
.
E)  .
.
7. f(x)=  функциясы үшін алғашқы функцияның жалпы түрін тап:
функциясы үшін алғашқы функцияның жалпы түрін тап:
A) x+lnsin4x+C
B) x+lncosx+C
C)  tg4x+C
tg4x+C
D) tg4x+C
E) tgx+C
8. f(x)=cos  3x-sin
3x-sin  3x функциясы үшін алғашқы функцияның жалпы түрін тап:
3x функциясы үшін алғашқы функцияның жалпы түрін тап:
A) 6sin6x+C
B) 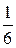 sin6x+C
sin6x+C
C) sin6x+C
D) - 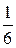 cos6x+C
cos6x+C
E) 6cos6x+C
9. f(x)= cos  x +sin
x +sin  x-5cos5x функциясы үшін алғашқы функцияның жалпы түрін тап:
x-5cos5x функциясы үшін алғашқы функцияның жалпы түрін тап:
A) x+cos5x+C
B) x+5cos5x+C
C) x+5sin5x+C
D) x-5cos5x+C
E) x-sin5x+C
10. y =  функциясының алғашқы функциясын табыңыз.
функциясының алғашқы функциясын табыңыз.
A)  + C
+ C
B)  + C
+ C
C) 2  + C
+ C
D) -  + C
+ C
E)  + C
+ C
11. f(x) = 6x + 4 функциясы үшін F(x) алғашқы функциясы болса, онда
F(x) = 0 теңдеуін шешіңіз, мұндағы F(-2) = 5
A)  .
.
B)  .
.
C)  .
.
D) 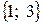 .
.
E)  .
.
12. Егер F(-3) = 2 болса, f(x) = x2 + 4x функциясы үшін алғашқы функцияны табыңыз.
A)  .
.
B)  .
.
C) 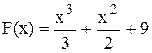 .
.
D)  .
.
E)  .
.
DEFINITE INTEGRAL 1
1. Есептеңіз:  .
.
A)  . B) 0. C)
. B) 0. C)  . D)
. D)  . E)
. E)  .
.
2. а-ның қандай мәндерінде  теңсіздігі орындалады?
теңсіздігі орындалады?
A) а ¹ ±p+2pn, n Î Z.
B) а ¹ p+2pn, n Î Z.
C) а ¹ ±  +pn, n Î Z.
+pn, n Î Z.
D) а ¹ 2pn, n Î Z.
E) а ¹  +pn, n Î Z.
+pn, n Î Z.
3. Интегралды есептеңіз: 
A) -13 B) 15 C) -11 D) 13 E) -15
4.  интегралын есептеңіз:
интегралын есептеңіз:
A)  B)
B)  C)
C)  D)
D)  E)
E) 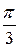
5.  интегралын есептеңіз:
интегралын есептеңіз:
A) 4  B) 5
B) 5  C) 3
C) 3  D) 2
D) 2  E)
E) 
6. а-ның қандай мәндерінде  теңсіздігі орындалады?
теңсіздігі орындалады?
A) (-¥; -  ).
).
B) (-¥;  ).
).
C) ( ; +¥).
; +¥).
D) (-  ;
;  ).
).
E) (-  ; +¥).
; +¥).
7.  интегралын есептеңіз:
интегралын есептеңіз:
A) 1  B) 1
B) 1  C) 1
C) 1 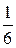 D) 1
D) 1  E) 1
E) 1 
8.  интегралын есептеңіз:
интегралын есептеңіз:
A) ln5 B) ln2 C) ln6 D) ln4 E) ln3
9. Есептеңіз:  .
.
A)  . B) -
. B) -  . C)
. C)  .
.
D) -  . E)
. E)  .
.
10. Есептеңіз:  .
.
A)  . B) 2. C) -
. B) 2. C) -  . D)
. D)  . E) 0.
. E) 0.
11.  интегралын есепте:
интегралын есепте:
A) ln2 B) ln5 C) ln3 D) 0 E) ln4
12.  интегралын есепте:
интегралын есепте:
A)  B)
B) 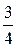 C) 0 D) 1 E)
C) 0 D) 1 E) 
13.  интегралын есепте:
интегралын есепте:
A) 4 B) 8 C) 2 D) 6 E) 5
14.  интегралын есепте:
интегралын есепте:
A) 2  B) 1
B) 1  C) 1
C) 1  D) 3
D) 3  E) 2
E) 2 
15. Есептеңіз: 
A) - 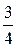 . B) 1
. B) 1  . C)
. C) 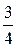 . D)
. D)  . E) -
. E) -  .
.
16. Интегралды есептеңіз: 
A) 23 B) 27 C) 21 D) 24 E) 18
17. Есептеңіз:  .
.
A) -  . B)
. B)  . C) 0. D) 2. E)
. C) 0. D) 2. E)  .
.
18.  интегралын есепте:
интегралын есепте:
A)  B) 0 C)
B) 0 C)  D) 1 E)
D) 1 E) 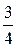
19.  интегралын есепте:
интегралын есепте:
A)2  B)1
B)1  C) 2
C) 2  D) 1
D) 1  E) 3
E) 3 
20. Есептеңіз:  .
.
A)  . B) -
. B) -  . C) -
. C) -  .
.
D)  . E)
. E)  .
.
Дата добавления: 2015-10-30; просмотров: 205 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| п.1. Метод подстановки (или замены в неопределенном интеграле). | | | По специальным разделам высшей математики |