п.1. Метод подстановки (или замены в неопределенном интеграле).

Пусть мы имеем интеграл .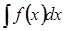

Введем новую переменную t, вместо x, положив x=j(t), где j(t) монотонна (из монотонности функции x=j(t) вытекает существование обратной функции t=Y(x)) и дифференцируема (из дифференцируемости следует непрерывность) тогда будет справедлива формула

действительно, используя свойство 2) неопределенного интеграла, продиференцируем обе части этого равенства. С одной стороны , а с другой, (т.к. ).

Таким образом, обе части формулы  имеют один и тот же дифференциал и потому выражают собой одно и то же семейство первообразных для функции ¦(x). это и доказывает равенство  в том смысле, что правая и левая части его могут отличатся между собой разве лишь на постоянное слагаемое.

Пример 1: вычислить интеграл

Здесь полезно применить подстановку , освобождающую нас от радикалов. Дифференцируем это равенство: .

Тогда

возвращаясь к старой переменной x,

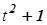
получим

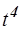
1

Замечание:

При замене переменной весьма часто бывает выгоднее задавать не x как функцию t, а, наоборот, задавать t как функцию от x и писать подстановку в виде t=Y(x). теоретически оба способа равнозначны, т.к. если функция x=j(x) монотонна, то всегда можно выразить t как функцию x и написать: t=Y(x) (или ). Однако при вычислении некоторых интегралов подстановка t=Y(x) может оказаться более удобной. К сожалению, нельзя дать общих правил, по которым следует выбирать ту или иную подстановку применительно к заданному интегралу; умение разыскивать удачные подстановки достигаются практикой.

Отдельные замечание, относящиеся к определенным типам подынтегральных выражений, будут сделаны ниже вместе с указанием типичных подстановок. Однако не следует слепо придерживаться какого-то раз навсегда установившегося шаблона в выборе подстановки. Весьма часто встречаются интегралы, которые могут быть вычислены с помощью различных подстановок, и искусство вычислителя состоит в том, чтобы применить ту из них, которая быстрее и проще ведет к цели.

Пример 2:

Подстановка , , дает

Вообще, если подынтегральное выражение не содержит других иррациональностей, кроме корня из линейной функции , то следует применять подстановку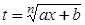

Дата добавления: 2015-10-30