Элементарная теория электропроводности полупроводников

Проведем подсчет плотности тока для донорного полупровод­ника, электроны проводимости которого будем рассматривать как идеальные частицы, не имеющие собственного объема и не взаимо­действующие друг с другом. Так как по классической теории радиус электрона r₀ ~10 ^-13 см, то при концентрации их п~ 10²² см³ объем электронов составляет — 4pr₀³ /3 ~ 10^{- 17} объема вещества и первое предположение вполне оправдано.

Предположим, что концентрация электронов проводимости n (количество свободных электронов в 1 см³ полупроводника), а ско­рость их дрейфового движения V. Поскольку плотность тока есть заряд, проходящий в единицу времени через единичное сечение площадки, перпендикулярной направлению скорости движения электронов, то

J= - qпV,(1.10)

Определение скорости дрейфа электронов проведем без учета (первый случай) и с учетом статистического разброса времени свободного пробега (второй случай).

В первом случае, предполагается, что время свободного электрона равно его усредненному значению. Пусть под действием внешнего электрического поля напряженности Е электроны с массой т и зарядом q получают ускорение

a = - qE/m (1.11)

и направленную добавку к скорости

DV = at = qtE/m, (1.12)

где t - время, в течение которого действует ускорение a. Если бы t не было ничем ограничено, то и скорость электронов в направлении поля неограниченно возрастала бы. В действительности это не так. В реальных кристаллах всегда существуют дефекты, ограничивающие длину свободного пробега, а, значит, и время, в течение которого электрону сообщается ускорение. Поэтому электрон лишь на сравнительно небольшом отрезке пути, равном длине свободного пробега, движется ускоренно, затем испытывает соударение, теряет при этом свою направленную скорость и весь процесс начинается снова.

Время свободного пробега, зная длину свободного пробега, можно определить на основании выражения:

t = l/V (1.13)

где V = V₀ + DV. Так как направленная добавка к скорости электрона DV при не очень сильных полях мала по сравнению со скоростью V₀ хаотического теплового движения электронов в отсутствие поля, то формулу (1.9) можно переписать в виде:

t = l/V₀ (1.14)

Средняя дрейфовая скорость, с которой электрон будет двигаться вдоль поля,

V = DV/2= qtE/2m (1.15)

Здесь мы учли, что в момент после столкновения начальная дрейфовая скорость равна нулю.

Второй случай. В действительности численные значения величин "время свободного пробега" и "среднее время свободного пробега" существенно различаются. Для учета статистического разброса времени свободного пробега сделаем следующее предположение. Пусть вероятность того, что электрон за время dt испытает столкновение (рассеяние) пропорциональна dt/t, где 1/t - неизвестный параметр. Кроме того, будем считать, что вероятность столкновения в единицу вре­мени1/tне зависит от времени, т. е.tесть некоторая постоян­ная величина.

Обозначим вероятность того, что электрон летел в течение времени t без столкновения p(t). Тогда вероятность того, что электрон пролетел время t без столкновения, а затем испытал столкновение за время dt будет равна произведению вероятностей этих двух событий:

dw(t) = p(t) dt/t (1.16)

Но это dw(t) и есть уменьшение p(t) за время dt:

dw(t) =- dp(t).

Следовательно,:

dp(t= - p(t) dt/t. (1.17)

Решая уравнение(10)относительно р, получаем:

р(t)=р₀ exp(- t/t), (1.18)

где р = р₀ при t=0.

Если начать отсчет с момента после столкновения, то р₀ = 1. Тогда

р(t)= exp(- t/t) (1.19)

Из последнего соотношения следует, что количество электронов, движущихся в данном направлении, в результате столкновений уменьшается по экспоненциальному закону с постоянной времени t.

Воспользовавшисьвыражением (12), среднее время свободного пробега электронов можно рассчитать по формуле:

(1.20)

Откуда следует, что t есть среднее время свободного пробега, то есть среднее время движения электронов между двумя соударениями.

Среднюю дрейфовую скорость определим аналогичным образом:

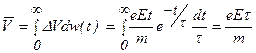(1.21)

Сравнивая формулы (8) и (14) следует, что учет непостоянства времени свободного пробега дает в два раза большую среднюю дрейфовую скорость электронов. Отметим, что в выражение (1.17) также входит величина t. Ее можно рассматривать как время релаксации системы.

Таким образом, как видно из соотношений (8) и (14), скорость дрейфа электронов пропорциональна напряженности электрического поля, времени свободного пробега и обратно-пропорциональна массе элек­трона.

Параметр, связывающий дрейфовую скорость носителей заряда с напряженностью электрического поля, называют подвижностью носителей заряда. Обозначим его m, тогда

V = mE, (1.22)

где, как следует из (14),

m =V/E = qt/m, (1.23)

то есть подвижность носителей заряда численно равна скорости дрейфа в электрическом поле единичной напряженности.

С учетом равенства (15) выражение (3) для плотности тока примет вид:

J = - qnV = qnmE (1.24)

так как вектор скорости электронов направлен в противоположную сторону вектора E.

Удельная проводимость на основании закона Ома может быть выражена при помощи (17) как

s= J/E = qnm_n, (1.25)

или s= e²nt/m

Аналогично может быть получено выражение для удельной проводимости полупроводника р-типа:

s= J/E = qрm_p (1.26)

В случае, если проводимость обусловлена переносом электронов и дырок, что имеет место, например, в собственных полупроводниках, выражение для удельной проводимости можно зависать в виде:

s= J/E = qрm_р+ qпm_п (1.27)

Из соотношения (19) следует, что в полупроводнике п -типа, где основными носителями являются электроны, дрейфовый ток, обусловленный неосновными носителями (дырками) пренебрежимо мал по сравнению с током, который связан с основными носителями.

Кроме этого, еще раз обращаю внимание на следующее: в полупроводнике п-типа, то есть легированном донорной примесью, вектор напряженности электрического поля и скорости электронов направлены в противоположные стороны, а в полупроводнике р-типа – вектор напряженности электрического поля и скорости дырок направлены одинаково.

Дата добавления: 2015-10-23