Электропроводность собственного полупроводника в рамках модели ковалентной связи

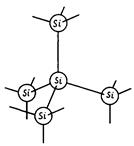
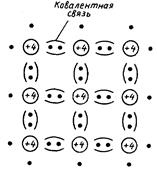
В кремнии каждый атом имеет четыре валентных электрона, являющихся общими для четырех ближайших атомов. Связь атома кремния с четырьмя соседними можно представить в виде, проиллюстрированном на рис. 1.31. Центральный атом кремния на схеме (а) соединен с соседними атомами химическими связями таким образом, что имеет место тетраэдрическое окружение (т.е. атом находится в центре тетраэдра). На рис. 1.31 (б) приведена упрощенная схема кристаллической решетки в виде двумерного изображения ковалентных связей в решетке кремния. Здесь в узле решетки находится ион кремния с зарядом +4, которому принадлежат четыре валентных электрона. Валентные электроны представлены в виде черных точек.

(а) (б) (в)

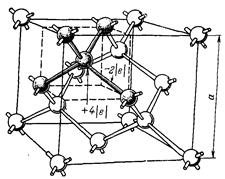
Рис. 1.31. Тетраэдрическое пространственное распределение атомов, в котором атом кремния связан с четырьмя соседними атомами (а), двумерная модель, в которой каждая связь образована двумя общими электронами (б) и распределение атомов и электронов в элементарной ячейке кристалла кремния (в).

В полупроводнике с иде­альной структурой, изобра­женной на рис. 1.31 (в), все электроны находятся в свя­занном состоянии. Если та­кой полупроводник поме­стить во внешнее электри­ческое поле, то электриче­ский ток не может возник­нуть, так как все ковалентные связи в решетке завершены и свободных носителей за­ряда нет.

Допустим, что при воз­действии каких-либо возму­щений, например теплоты, в полупроводнике произо­шел разрыв ковалентной связи и электрон стал свободным. Процесс превращения связанного электрона в свободный электрон носит название генерации. При уходе электрона ковалентная связь будет незавершенной. Неза­вершенная связь будет иметь избыточный положительный заряд, поскольку теперь он не скомпенсирован зарядом электрона. Освободившееся таким образом место в ковалентной связи получило название дырки. В целом кристалл остается электронейтральным, так как каждому образо­вавшемуся положительному заряду в связи — дырке соответствует свободный электрон. На рис. 1.32, б свободные электроны и дырки изображены соответственно черными и светлыми кружочками. Свободный электрон может занять вакантное место в ковалентной связи и перейти в связанное состояние. Процесс превращения свободного электрона в связанный электрон, носит название рекомбинации.

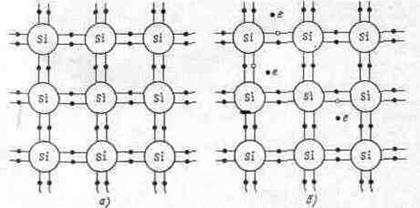
Рис. 1.32. Образование (генерация) свободных носителей заряда – электронов и дырок – в нелегированном (собственном) полупроводнике.

Следовательно, собственный полупроводник — идеально чистое вещество, в котором в результате разрыва ковалентных связей обра­зуется равное количество свободных, электронов и дырок. При комнат­ной температуре концентрация свободных электронов и дырок в германии составляет примерно 10¹³ см ^-3, а у кремния — около 10¹⁰ см^-3. Увеличение температуры полупроводника приводит к воз­растанию количества разорванных ковалентных связей, а следова­тельно, к росту концентрации свободных электронов и дырок в по­лупроводнике.

В отсутствие внешнего электрического поля свободный электрон, совершая тепловое движение в кристалле полупроводника, будет сталкиваться с дефектами кристаллической решетки, в результате чего меняется направление его движения. В силу этого тепловое движение свободного электрона является беспорядочным, как это изображено на рис. 1.33 (а).

Вакантное место в ковалентной связи — дырка может быть за­полнена электроном, перешедшим вследствие теплового возбужде­ния с соседней насыщенной ковалентной связи. При таком переходе от атома к атому дырка также будет совершать хаотическое дви­жение.

Таким образом, тепловое движение свободных носителей заряда в кристалле полупроводника является беспорядочным. При этом каждый из носителей заряда описывает сложную траекторию дви­жения ( рис. 1.33 (а)).

(а) (б)

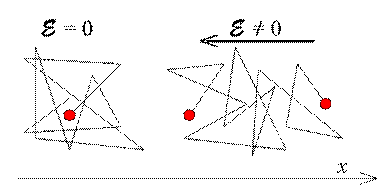
Рис. 1.33. Схема движения свободного электрона при отсутствии (а) и наличии внешнего электрического поля (б)

Расстояние, проходимое свободным носителем заряда между двумя столкновениями, называют, длиной свободного пробега, а усредненное значение всех отрезков пути, пройденного носителем, есть средняя длина свободного пробега. Соответственно время между двумя соударениями и его усредненное значение назы­вают временем свободного пробега и средним временем свободного пробега.

Средняя длина свободного пробега l и среднее время свободного пробега t связаны соотношением:

l=V₀t (1.9)

где V₀ - скорость теплового движении свободного носителя заряда (среднее значение модуля скорости).

В полупроводниках при комнатной температуре скорость тепло­вого движения электронов порядка 10⁷ см/с. Длина свободного пробега составляет 10^-6 -10^{-4 см. Следовательно, время свободного пробега оказывается порядка 10-13} – 10^-11 с.

Поскольку тепловое движение свободных носителей заряда — электронов и дырок — является беспорядочным, то их средняя ско­рость, рассматриваемая как векторная величина, равна нулю. Это означает, что каждому движущемуся свободному электрону (дырки) можно сопоставить свободный электрон (дырку), перемещающийся в противоположную сторону с такой же скоростью (рис. Рис. 1.34, а}. Следовательно, вследствие беспорядочного теплового движения количество свободных электронов и дырок, движущихся в любом направлении, в среднем равно числу электронов и дырок, движу­щихся в противоположном направлении. Поэтому в отсутствие внеш­него электрического поля суммарный заряд, переносимый свобод­ными электронами и дырками в любом направлении, равен нулю, а, значит, беспорядочное тепловое движение носителей заряда не дает тока.

Если собственный полупроводник находится во внешнем электрическом поле, то под воздействием этого поля свободные электроны приобретут скорость, направленную против поля. Благодаря этому у электронов, тепловое движение которых происходило против направления внешнего электрического поля, скорость увеличится, а у электронов, движущихся в направлении поля, умень­шится.

В результате вся совокупность свободных электронов получает некоторую скорость движения в направлении, противоположном направлению внешнего электрического поля (Рис. 1.34, б). Измене­ние скорости движения электронов скажется на их кинетической энергии. При столкновении с дефектами кристаллической решетки электроны передают решетке всю энергию, приобретенную в поле, вследствие чего они "придут в тепловое равновесие с решеткой. После столкновения электроны, совершая хаотическое тепловое движение, опять будут иметь направленное движение во внешнем электрическом поле.

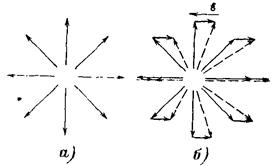
Рис. 1.34. Схематическое изображение скорости электронов проводимости при отсутствии (а) и наличии (б) внешнего электрического поля

Таким образом, фактическое движение электрона в кристалле складывается из беспорядочного теплового и упорядоченного движе­ния, вызванного действием внешнего электрического поля (рис. 1.34., б). В результате этого происходит медленное перемещение всей сово­купности свободных электронов с некоторой средней скоростью. Направленное движение совокупности свободных носителей заряда во внешнем электрическом поле носит название дрейфа, а скорость их, направленного движения называют дрейфовой. На рис. 1.34., б горизонтальными линиями изображены векторы дрейфовой ско­рости, а пунктиром — векторы суммарной скорости теплового дви­жения и дрейфа. В этом случае средняя скорость движения свобод­ных электронов уже не равна нулю и через полупроводник в напра­влении электрического поля потечет ток, обусловленный свобод­ными электронами.

Электроны насыщенных связей при переходе в вакантное место в связи под действием внешнего электрического поля будут перемещаться против направления поля. Тем самым вакантное место в ковалентной связи — дырка будет переме­щаться, но по направлению внешнего электрического поля, что равносильно перемещению по полю положительного заряда. Механизм электропроводности, обусловленный движением электроновпосвободным местам в ковалентных связях, получил название дырочной электропро­водности.

Таким образом, в чистом полупроводнике, не содержащем приме­сей, осуществляется электронная и дырочная электропроводность. Следовательно, электрический ток в собственном полупроводнике определяется двумя составляющими — электронным и дырочным токами, текущими в одном направлении.

Дата добавления: 2015-10-23